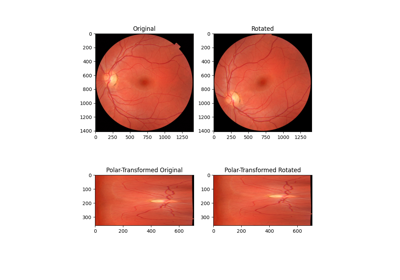
skimage.registration#

图像配准算法，例如光流或相位互相关。

optical_flow_ilk

粗到精光流估计器。

optical_flow_tvl1

粗到精光流估计器。

phase_cross_correlation

通过互相关实现高效的亚像素图像平移配准。
skimage.registration.optical_flow_ilk(reference_image, moving_image, *, radius=7, num_warp=10, gaussian=False, prefilter=False, dtype=<class 'numpy.float32'>)[源代码]#

粗到精光流估计器。

迭代 Lucas-Kanade (iLK) 求解器应用于图像金字塔的每个级别。iLK [1] 是一种快速且稳健的 TVL1 算法替代方案，尽管在渲染平面和对象边界时精度较低（参见 [2]）。

参数:
reference_imagendarray，形状 (M, N[, P[, …]])

序列的第一个灰度图像。

moving_imagendarray，形状 (M, N[, P[, …]])

序列的第二个灰度图像。

radiusint，可选

考虑每个像素周围的窗口半径。

num_warpint，可选

移动图像被扭曲的次数。

gaussianbool，可选

如果为 True，则使用高斯核进行局部积分。否则，使用均匀核。

prefilterbool，可选

是否在每次图像扭曲之前预过滤估计的光流。如果为 True，则应用沿每个轴窗口大小为 3 的中值滤波器。这有助于消除潜在的异常值。

dtypedtype，可选

输出数据类型：必须是浮点数。与双精度相比，单精度可提供良好的结果，并节省内存使用和计算时间。

返回:
flowndarray，形状 (reference_image.ndim, M, N[, P[, …]])

每个轴的估计光流分量。

注释

  • 实现的算法在 [1] 的表 2 中描述。

  • 不支持彩色图像。

参考文献

[1] (1,2)

Le Besnerais, G., & Champagnat, F. (2005, September). Dense optical flow by iterative local window registration. In IEEE International Conference on Image Processing 2005 (Vol. 1, pp. I-137). IEEE. DOI:10.1109/ICIP.2005.1529706

[2]

Plyer, A., Le Besnerais, G., & Champagnat, F. (2016). Massively parallel Lucas Kanade optical flow for real-time video processing applications. Journal of Real-Time Image Processing, 11(4), 713-730. DOI:10.1007/s11554-014-0423-0

示例

>>> from skimage.color import rgb2gray
>>> from skimage.data import stereo_motorcycle
>>> from skimage.registration import optical_flow_ilk
>>> reference_image, moving_image, disp = stereo_motorcycle()
>>> # --- Convert the images to gray level: color is not supported.
>>> reference_image = rgb2gray(reference_image)
>>> moving_image = rgb2gray(moving_image)
>>> flow = optical_flow_ilk(moving_image, reference_image)

使用光流进行配准

使用光流进行配准
skimage.registration.optical_flow_tvl1(reference_image, moving_image, *, attachment=15, tightness=0.3, num_warp=5, num_iter=10, tol=0.0001, prefilter=False, dtype=<class 'numpy.float32'>)[源代码]#

粗到精光流估计器。

TV-L1 求解器应用于图像金字塔的每个级别。TV-L1 是 Zach 等人引入的流行的光流估计算法。 [1]，在 [2] 中改进并在 [3] 中详细介绍。

参数:
reference_imagendarray，形状 (M, N[, P[, …]])

序列的第一个灰度图像。

moving_imagendarray，形状 (M, N[, P[, …]])

序列的第二个灰度图像。

attachmentfloat，可选

附加参数（\(\lambda\) 在 [1] 中）。此参数越小，返回的结果将越平滑。

tightnessfloat，可选

紧密度参数（\(\theta\) 在 [1] 中）。它应该具有较小的值，以保持附件和正则化部分的对应关系。

num_warpint，可选

移动图像被扭曲的次数。

num_iterint，可选

定点迭代次数。

tolfloat，可选

公差用作基于 (u, v) 的两个连续值之间的 L² 距离的停止标准。

prefilterbool，可选

是否在每次图像扭曲之前预过滤估计的光流。如果为 True，则应用沿每个轴窗口大小为 3 的中值滤波器。这有助于消除潜在的异常值。

dtypedtype，可选

输出数据类型：必须是浮点数。与双精度相比，单精度可提供良好的结果，并节省内存使用和计算时间。

返回:
flowndarray，形状 (image0.ndim, M, N[, P[, …]])

每个轴的估计光流分量。

注释

不支持彩色图像。

参考文献

[1] (1,2,3)

Zach, C., Pock, T., & Bischof, H. (2007, September). A duality based approach for realtime TV-L 1 optical flow. In Joint pattern recognition symposium (pp. 214-223). Springer, Berlin, Heidelberg. DOI:10.1007/978-3-540-74936-3_22

[2]

Wedel, A., Pock, T., Zach, C., Bischof, H., & Cremers, D. (2009). An improved algorithm for TV-L 1 optical flow. In Statistical and geometrical approaches to visual motion analysis (pp. 23-45). Springer, Berlin, Heidelberg. DOI:10.1007/978-3-642-03061-1_2

[3]

Pérez, J. S., Meinhardt-Llopis, E., & Facciolo, G. (2013). TV-L1 optical flow estimation. Image Processing On Line, 2013, 137-150. DOI:10.5201/ipol.2013.26

示例

>>> from skimage.color import rgb2gray
>>> from skimage.data import stereo_motorcycle
>>> from skimage.registration import optical_flow_tvl1
>>> image0, image1, disp = stereo_motorcycle()
>>> # --- Convert the images to gray level: color is not supported.
>>> image0 = rgb2gray(image0)
>>> image1 = rgb2gray(image1)
>>> flow = optical_flow_tvl1(image1, image0)

使用光流进行配准

使用光流进行配准
skimage.registration.phase_cross_correlation(reference_image, moving_image, *, upsample_factor=1, space='real', disambiguate=False, reference_mask=None, moving_mask=None, overlap_ratio=0.3, normalization='phase')[源代码]#

通过互相关实现高效的亚像素图像平移配准。

此代码在计算时间的一小部分和减少的内存需求下提供了与 FFT 上采样互相关相同的精度。它通过 FFT 获得互相关峰值的初始估计，然后通过矩阵乘法 DFT [1]，仅在该估计的小邻域内上采样 DFT 来细化偏移估计。

参数:
reference_image数组

参考图像。

moving_image数组

要配准的图像。必须与 reference_image 具有相同的维度。

upsample_factorint，可选

上采样因子。图像配准的精度将达到像素的 1 / upsample_factor。例如，upsample_factor == 20 表示图像配准的精度将达到 1/20 个像素。默认值为 1 (不进行上采样)。如果 reference_mask 或 moving_mask 中任何一个不为 None，则不使用此参数。

spacestring, 可选，取值为 “real” 或 “fourier”

定义算法如何解释输入数据。“real” 表示数据将进行 FFT 计算相关性，而 “fourier” 表示数据将绕过输入数据的 FFT。不区分大小写。如果 reference_mask 或 moving_mask 中任何一个不为 None，则不使用此参数。

disambiguatebool

由于傅里叶变换的周期性，此函数返回的位移仅在图像形状的模意义上是准确的。如果此参数设置为 True，则将计算每个可能位移的实空间互相关，并返回重叠区域内具有最高互相关的位移。

reference_maskndarray

用于 reference_image 的布尔掩码。掩码应在有效像素上评估为 True（或 1）。reference_mask 应具有与 reference_image 相同的形状。

moving_maskndarray 或 None, 可选

用于 moving_image 的布尔掩码。掩码应在有效像素上评估为 True（或 1）。moving_mask 应具有与 moving_image 相同的形状。如果为 None，则将使用 reference_mask。

overlap_ratiofloat, 可选

图像之间允许的最小重叠比率。将忽略重叠比率低于此阈值的平移的相关性。较低的 overlap_ratio 会导致最大平移较小，而较高的 overlap_ratio 会提高在蒙版图像之间重叠较小时对虚假匹配的鲁棒性。仅当 reference_mask 或 moving_mask 中任何一个不为 None 时才使用。

normalization{“phase”, None}

应用于互相关的归一化类型。当提供掩码（reference_mask 和 moving_mask）时，不使用此参数。

返回:
shiftndarray

将 moving_image 与 reference_image 配准所需的位移向量（以像素为单位）。轴顺序与输入数组的轴顺序一致。

errorfloat

reference_image 和 moving_image 之间的平移不变归一化 RMS 误差。对于掩码互相关，此误差不可用，返回 NaN。

phasedifffloat

两幅图像之间的全局相位差（如果图像为非负，则应为零）。对于掩码互相关，此相位差不可用，返回 NaN。

注释

使用互相关来估计图像平移的历史可以追溯到至少 [2]。“相位相关”方法（通过 normalization="phase" 选择）最早在 [3] 中提出。出版物 [1] 和 [2] 使用未归一化的互相关 (normalization=None)。哪种归一化形式更好取决于具体应用。例如，相位相关方法在不同光照下配准图像效果良好，但对噪声的鲁棒性不强。在高噪声情况下，未归一化方法可能更可取。

当提供掩码时，使用掩码归一化互相关算法 [5], [6]。

参考文献

[1] (1,2)

Manuel Guizar-Sicairos, Samuel T. Thurman, and James R. Fienup, “Efficient subpixel image registration algorithms,” Optics Letters 33, 156-158 (2008). DOI:10.1364/OL.33.000156

[2] (1,2)

P. Anuta, Spatial registration of multispectral and multitemporal digital imagery using fast Fourier transform techniques, IEEE Trans. Geosci. Electron., vol. 8, no. 4, pp. 353–368, Oct. 1970. DOI:10.1109/TGE.1970.271435.

[3]

C. D. Kuglin D. C. Hines. The phase correlation image alignment method, Proceeding of IEEE International Conference on Cybernetics and Society, pp. 163-165, New York, NY, USA, 1975, pp. 163–165.

[4]

James R. Fienup, “Invariant error metrics for image reconstruction” Optics Letters 36, 8352-8357 (1997). DOI:10.1364/AO.36.008352

[5]

Dirk Padfield. Masked Object Registration in the Fourier Domain. IEEE Transactions on Image Processing, vol. 21(5), pp. 2706-2718 (2012). DOI:10.1109/TIP.2011.2181402

[6]

D. Padfield. “Masked FFT registration”. In Proc. Computer Vision and Pattern Recognition, pp. 2918-2925 (2010). DOI:10.1109/CVPR.2010.5540032

图像配准

图像配准

掩码归一化互相关

掩码归一化互相关

使用极坐标和对数极坐标变换进行配准

使用极坐标和对数极坐标变换进行配准