skimage.measure#
测量图像属性,例如区域属性、轮廓。
使用指定的容差近似多边形链。 |
|
通过将函数 |
|
计算一个指标,指示图像中模糊的强度(0 表示无模糊,1 表示最大模糊)。 |
|
返回图像的(加权)质心。 |
|
计算二值图像中的欧拉特征。 |
|
在 2D 数组中查找给定级别值的等值轮廓。 |
|
测试指定网格上的点是否在多边形内。 |
|
计算输入图像的惯性张量。 |
|
计算图像惯性张量的特征值。 |
|
一个通道的分割二值掩码与第二个通道的分割二值掩码重叠的比例。 |
|
标记整数数组的连接区域。 |
|
两个通道之间的曼德斯共定位系数。 |
|
曼德斯重叠系数 |
|
Marching Cubes 算法用于在 3D 体积数据中查找曲面。 |
|
计算给定顶点和三角形面的表面积。 |
|
计算直到某个阶数的所有原始图像矩。 |
|
计算直到某个阶数的所有中心图像矩。 |
|
计算直到某个阶数的所有原始图像矩。 |
|
计算直到某个阶数的所有中心图像矩。 |
|
计算 Hu 的图像矩集(仅限 2D)。 |
|
计算直到某个阶数的所有归一化中心图像矩。 |
|
计算通道中像素强度之间的皮尔逊相关系数。 |
|
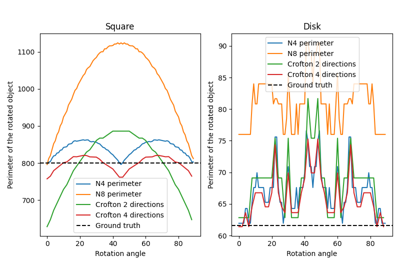
计算二值图像中所有对象的总周长。 |
|
计算二值图像中所有对象的总克罗夫顿周长。 |
|
测试点是否位于多边形内。 |
|
返回沿扫描线测量的图像的强度轮廓。 |
|
使用 RANSAC(随机抽样一致)算法将模型拟合到数据。 |
|
测量标记图像区域的属性。 |
|
计算图像属性并将其作为与 pandas 兼容的表格返回。 |
|
计算图像的香农熵。 |
|
使用 B 样条细分多边形曲线。 |
|
二维圆的总最小二乘估计器。 |
|
二维椭圆的总最小二乘估计器。 |
|
N 维直线的总最小二乘估计器。 |
- skimage.measure.approximate_polygon(coords, tolerance)[source]#
使用指定的容差近似多边形链。
它基于 Douglas-Peucker 算法。
请注意,近似多边形始终在原始多边形的凸包内。
- 参数:
- coords(K, 2) 数组
坐标数组。
- tolerancefloat
从多边形的原始点到近似多边形链的最大距离。如果容差为 0,则返回原始坐标数组。
- 返回:
- coords(L, 2) 数组
近似多边形链,其中 L <= K。
参考
- skimage.measure.block_reduce(image, block_size=2, func=<function sum>, cval=0, func_kwargs=None)[source]#
通过将函数
func应用于局部块来下采样图像。此函数对于最大池化和平均池化很有用,例如。
- 参数:
- image(M[, …]) ndarray
N 维输入图像。
- block_size类数组或 int
包含沿每个轴的下采样整数因子的数组。默认的 block_size 为 2。
- func可调用
函数对象,用于计算每个局部块的返回值。此函数必须实现
axis参数。主要函数是numpy.sum、numpy.min、numpy.max、numpy.mean和numpy.median。另请参阅func_kwargs。- cvalfloat
如果图像不能被块大小完美整除,则为常量填充值。
- func_kwargsdict
传递给
func的关键字参数。对于将 dtype 参数传递给np.mean特别有用。采用输入的字典,例如:func_kwargs={'dtype': np.float16})。
- 返回:
- imagendarray
下采样图像,其维度数与输入图像相同。
示例
>>> from skimage.measure import block_reduce >>> image = np.arange(3*3*4).reshape(3, 3, 4) >>> image array([[[ 0, 1, 2, 3], [ 4, 5, 6, 7], [ 8, 9, 10, 11]], [[12, 13, 14, 15], [16, 17, 18, 19], [20, 21, 22, 23]], [[24, 25, 26, 27], [28, 29, 30, 31], [32, 33, 34, 35]]]) >>> block_reduce(image, block_size=(3, 3, 1), func=np.mean) array([[[16., 17., 18., 19.]]]) >>> image_max1 = block_reduce(image, block_size=(1, 3, 4), func=np.max) >>> image_max1 array([[[11]], [[23]], [[35]]]) >>> image_max2 = block_reduce(image, block_size=(3, 1, 4), func=np.max) >>> image_max2 array([[[27], [31], [35]]])
- skimage.measure.blur_effect(image, h_size=11, channel_axis=None, reduce_func=<function max>)[source]#
计算一个指标,指示图像中模糊的强度(0 表示无模糊,1 表示最大模糊)。
- 参数:
- imagendarray
RGB 或灰度 nD 图像。输入图像在计算模糊度量之前转换为灰度。
- h_sizeint,可选
重新模糊滤波器的大小。
- channel_axisint 或 None,可选
如果为 None,则假定图像为灰度(单通道)。否则,此参数指示数组的哪个轴对应于颜色通道。
- reduce_func可调用,可选
用于计算沿所有轴的模糊度量聚合的函数。如果设置为 None,则返回整个列表,其中第 i 个元素是沿第 i 个轴的模糊度量。
- 返回:
- blur浮点数(0 到 1)或浮点数列表
模糊度量:默认情况下,是沿所有轴的模糊度量的最大值。
备注
h_size必须保持相同的值,以便比较图像之间的结果。大多数情况下,默认大小 (11) 就足够了。这意味着该度量可以清楚地辨别高达平均 11x11 滤波器的模糊;如果模糊更高,该度量仍然给出良好的结果,但其值趋向于渐近线。参考
[1]Frederique Crete、Thierry Dolmiere、Patricia Ladret 和 Marina Nicolas “模糊效应:使用新的无参考感知模糊度量进行感知和估计” Proc. SPIE 6492,人类视觉和电子成像 XII,64920I (2007) https://hal.archives-ouvertes.fr/hal-00232709 DOI:10.1117/12.702790
- skimage.measure.centroid(image, *, spacing=None)[source]#
返回图像的(加权)质心。
- 参数:
- image数组
输入图像。
- spacing: float 元组,形状 (ndim,)
图像沿每个轴的像素间距。
- 返回:
- 中心浮点数元组,长度为
image.ndim image中(非零)像素的质心。
- 中心浮点数元组,长度为
示例
>>> image = np.zeros((20, 20), dtype=np.float64) >>> image[13:17, 13:17] = 0.5 >>> image[10:12, 10:12] = 1 >>> centroid(image) array([13.16666667, 13.16666667])
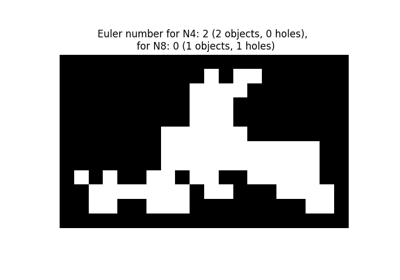
- skimage.measure.euler_number(image, connectivity=None)[源代码]#
计算二值图像中的欧拉特征。
对于 2D 对象,欧拉数是对象数量减去孔的数量。对于 3D 对象,欧拉数是对象数量加上孔的数量,减去隧道或环的数量。
- 参数:
- image: (M, N[, P]) ndarray
输入图像。如果图像不是二值的,则所有大于零的值都视为对象。
- 连通性int, 可选
将像素/体素视为邻居时要考虑的最大正交跳数。接受的值范围从 1 到 input.ndim。如果
None,则使用input.ndim的完全连通性。对于 2D 图像,定义了 4 或 8 邻域(分别为连通性 1 和 2)。对于 3D 图像,定义了 6 或 26 邻域(分别为连通性 1 和 3)。未定义连通性 2。
- 返回:
- euler_numberint
图像中所有对象集合的欧拉特性。
备注
欧拉特性是一个整数,描述输入图像中所有对象集合的拓扑结构。如果对象是 4 连通的,则背景是 8 连通的,反之亦然。
欧拉特性的计算基于离散空间中的积分几何公式。实际上,构造邻域配置,并对每个配置应用 LUT。使用的系数是 Ohser 等人的系数。
计算几种连通性的欧拉特性可能会很有用。不同连通性结果之间的较大相对差异表明图像分辨率(相对于对象和孔的大小)太低。
参考
[1]S. Rivollier. Analyse d’image geometrique et morphometrique par diagrammes de forme et voisinages adaptatifs generaux. PhD thesis, 2010. Ecole Nationale Superieure des Mines de Saint-Etienne. https://tel.archives-ouvertes.fr/tel-00560838
[2]Ohser J., Nagel W., Schladitz K. (2002) The Euler Number of Discretized Sets - On the Choice of Adjacency in Homogeneous Lattices. In: Mecke K., Stoyan D. (eds) Morphology of Condensed Matter. Lecture Notes in Physics, vol 600. Springer, Berlin, Heidelberg.
示例
>>> import numpy as np >>> SAMPLE = np.zeros((100,100,100)); >>> SAMPLE[40:60, 40:60, 40:60]=1 >>> euler_number(SAMPLE) 1... >>> SAMPLE[45:55,45:55,45:55] = 0; >>> euler_number(SAMPLE) 2... >>> SAMPLE = np.array([[0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 1, 1, 0, 0, 0, 0, 0], ... [0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0], ... [0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0], ... [0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0], ... [0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0], ... [0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0], ... [0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0], ... [1, 0, 1, 0, 0, 1, 1, 0, 1, 1, 0, 0, 1, 1, 1, 1, 1, 0], ... [0, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 0, 0, 0, 1, 1, 1, 1], ... [0, 1, 1, 0, 0, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1]]) >>> euler_number(SAMPLE) # doctest: 0 >>> euler_number(SAMPLE, connectivity=1) # doctest: 2
- skimage.measure.find_contours(image, level=None, fully_connected='low', positive_orientation='low', *, mask=None)[源代码]#
在 2D 数组中查找给定级别值的等值轮廓。
使用“行进正方形”方法计算输入 2D 数组在特定级别值下的等值轮廓。对数组值进行线性插值,以便为输出轮廓提供更好的精度。
- 参数:
- image(M, N) 双精度 ndarray
在其中查找轮廓的输入图像。
- levelfloat,可选
在数组中查找轮廓的值。默认情况下,级别设置为 (max(image) + min(image)) / 2
在 0.18 版本中更改: 此参数现在是可选的。
- fully_connectedstr, {‘low’, ‘high’}
指示低于给定级别值的数组元素是否被认为是完全连接的(因此,高于该值的元素将仅是面连接的),反之亦然。(有关详细信息,请参见下面的注释。)
- positive_orientationstr, {‘low’, ‘high’}
指示输出轮廓是否会在低值或高值元素的岛屿周围产生正向的多边形。如果为“low”,则轮廓将围绕低于等值线的元素逆时针缠绕。或者,这意味着低值元素始终位于轮廓的左侧。(有关详细信息,请参见下文。)
- mask(M, N) 布尔值 ndarray 或 None
一个布尔掩码,在需要绘制轮廓的位置为 True。请注意,NaN 值始终排除在考虑区域之外(无论
array为NaN,mask都会设置为False)。
- 返回:
- contours(K, 2) ndarray 列表
每个轮廓都是一个
(row, column)轮廓坐标的 ndarray。
备注
行进正方形算法是行进立方体算法 [1] 的一个特例。 此处提供了一个简单的解释
https://users.polytech.unice.fr/~lingrand/MarchingCubes/algo.html
行进正方形算法中存在一个不明确的情况:当给定的
2 x 2元素正方形有两个高值元素和两个低值元素,每对元素都以对角方式相邻。(其中高值和低值是相对于所寻求的轮廓值而言的。)在这种情况下,可以通过分隔低值元素的薄地峡将高值元素“连接在一起”,反之亦然。当元素跨对角线连接在一起时,它们被认为是“完全连接的”(也称为“面+顶点连接”或“8 连接”)。只有高值或低值元素可以是完全连接的,另一组将被视为“面连接”或“4 连接”。默认情况下,低值元素被认为是完全连接的;可以使用“fully_connected”参数来更改此设置。不保证输出轮廓是闭合的:与数组边缘或掩盖区域(mask 为 False 或 array 为 NaN 的区域)相交的轮廓将保持打开状态。所有其他轮廓将是闭合的。(可以通过检查起始点是否与结束点相同来测试轮廓的闭合性。)
轮廓是有方向的。默认情况下,低于轮廓值的数组值位于轮廓的左侧,而大于轮廓值的数组值位于轮廓的右侧。这意味着轮廓将围绕低值像素的岛屿逆时针缠绕(即以“正方向”)。可以使用“positive_orientation”参数来更改此行为。
输出列表中轮廓的顺序由轮廓中最小
x,y(按字典顺序)坐标的位置决定。这是输入数组遍历方式的副作用,但可以依赖它。警告
数组坐标/值假定为引用数组元素的中心。以一个简单的示例输入为例:
[0, 1]。此数组中 0.5 的插值位置是 0 元素(在x=0处)和 1 元素(在x=1处)之间的中间位置,因此将落在x=0.5处。这意味着,要找到合理的轮廓,最好在预期的“亮”和“暗”值之间的中间位置找到轮廓。特别是,给定一个二值化数组,不要选择在数组的低值或高值处查找轮廓。这通常会产生退化的轮廓,尤其是在单个数组元素宽度的结构周围。相反,请像上面一样选择一个中间值。
参考
[1]Lorensen, William and Harvey E. Cline. Marching Cubes: A High Resolution 3D Surface Construction Algorithm. Computer Graphics (SIGGRAPH 87 Proceedings) 21(4) July 1987, p. 163-170). DOI:10.1145/37401.37422
示例
>>> a = np.zeros((3, 3)) >>> a[0, 0] = 1 >>> a array([[1., 0., 0.], [0., 0., 0.], [0., 0., 0.]]) >>> find_contours(a, 0.5) [array([[0. , 0.5], [0.5, 0. ]])]
- skimage.measure.grid_points_in_poly(shape, verts, binarize=True)[源代码]#
测试指定网格上的点是否在多边形内。
对于网格上的每个
(r, c)坐标,即(0, 0)、(0, 1)等,测试该点是否位于多边形内。可以使用
binarize标志控制输出类型。有关更多详细信息,请参阅其文档。- 参数:
- shapetuple (M, N)
网格的形状。
- verts(V, 2) 数组
指定多边形的 V 个顶点,按顺时针或逆时针方向排序。第一个点可以(但不需要)重复。
- binarize: bool
如果
True,则函数的输出是布尔掩码。否则,它是标记数组。标签为:O - 外部,1 - 内部,2 - 顶点,3 - 边缘。
- 返回:
- mask(M, N) ndarray
如果
binarize为 True,则输出为布尔掩码。True 表示对应的像素位于多边形内部。如果binarize为 False,则输出为带标签的数组,像素的标签值介于 0 和 3 之间。这些值的含义是:0 - 外部,1 - 内部,2 - 顶点,3 - 边缘。
另请参阅
- skimage.measure.inertia_tensor(image, mu=None, *, spacing=None)[source]#
计算输入图像的惯性张量。
- 参数:
- image数组
输入图像。
- mu数组,可选
预先计算的
image的中心矩。惯性张量的计算需要图像的中心矩。如果应用程序同时需要中心矩和惯性张量(例如,skimage.measure.regionprops),那么预先计算它们并将它们传递给惯性张量调用会更有效率。- spacing: float 元组,形状 (ndim,)
图像沿每个轴的像素间距。
- 返回:
- T数组,形状为
(image.ndim, image.ndim) 输入图像的惯性张量。\(T_{i, j}\) 包含图像强度沿轴 \(i\) 和 \(j\) 的协方差。
- T数组,形状为
参考
[2]Bernd Jähne. 时空图像处理:理论和科学应用。(第 8 章:张量方法) Springer, 1993。
- skimage.measure.inertia_tensor_eigvals(image, mu=None, T=None, *, spacing=None)[source]#
计算图像惯性张量的特征值。
惯性张量测量图像强度沿图像轴的协方差。(参见
inertia_tensor。)因此,张量的特征值的相对大小是衡量图像中(明亮)物体伸长率的指标。- 参数:
- image数组
输入图像。
- mu数组,可选
预先计算的
image的中心矩。- T数组,形状为
(image.ndim, image.ndim) 预先计算的惯性张量。如果给定了
T,则会忽略mu和image。- spacing: float 元组,形状 (ndim,)
图像沿每个轴的像素间距。
- 返回:
- eigvals浮点数列表,长度为
image.ndim image的惯性张量的特征值,按降序排列。
- eigvals浮点数列表,长度为
备注
计算特征值需要输入图像的惯性张量。如果提供了中心矩(
mu),或者,也可以直接提供惯性张量(T),则速度会快得多。
- skimage.measure.intersection_coeff(image0_mask, image1_mask, mask=None)[source]#
一个通道的分割二值掩码与第二个通道的分割二值掩码重叠的部分。
- 参数:
- image0_mask(M, N) dtype 为 bool 的 ndarray
通道 A 的图像掩码。
- image1_mask(M, N) dtype 为 bool 的 ndarray
通道 B 的图像掩码。必须与
image0_mask具有相同的维度。- mask(M, N) dtype 为 bool 的 ndarray,可选
计算中仅包含此感兴趣区域掩码内的
image0_mask和image1_mask像素。必须与image0_mask具有相同的维度。
- 返回:
- 交集系数,浮点数
image0_mask与image1_mask重叠的部分。
- skimage.measure.label(label_image, background=None, return_num=False, connectivity=None)[source]#
标记整数数组的连接区域。
当两个像素是邻居并且具有相同的值时,它们是连接的。在 2D 中,它们可以是 1 连接或 2 连接的邻居。该值是指将像素/体素视为邻居时要考虑的最大正交跳数。
1-connectivity 2-connectivity diagonal connection close-up [ ] [ ] [ ] [ ] [ ] | \ | / | <- hop 2 [ ]--[x]--[ ] [ ]--[x]--[ ] [x]--[ ] | / | \ hop 1 [ ] [ ] [ ] [ ]
- 参数:
- label_imagedtype 为 int 的 ndarray
要标记的图像。
- backgroundint,可选
将所有具有此值的像素视为背景像素,并将它们标记为 0。默认情况下,将值为 0 的像素视为背景像素。
- return_numbool,可选
是否返回分配的标签数量。
- 连通性int, 可选
将像素/体素视为邻居时要考虑的最大正交跳数。接受的值范围从 1 到 input.ndim。如果为
None,则使用input.ndim的完全连通性。
- 返回:
- labelsdtype 为 int 的 ndarray
标记数组,其中所有连接的区域都被分配相同的整数值。
- numint,可选
标签的数量,等于最大标签索引,只有当 return_num 为
True时才会返回。
参考
[1]Christophe Fiorio 和 Jens Gustedt,“图像处理的两种线性时间 Union-Find 策略”,理论计算机科学 154 (1996),第 165-181 页。
[2]Kensheng Wu、Ekow Otoo 和 Arie Shoshani,“优化连通分量标记算法”,论文 LBNL-56864,2005 年,劳伦斯伯克利国家实验室(加利福尼亚大学),http://repositories.cdlib.org/lbnl/LBNL-56864
示例
>>> import numpy as np >>> x = np.eye(3).astype(int) >>> print(x) [[1 0 0] [0 1 0] [0 0 1]] >>> print(label(x, connectivity=1)) [[1 0 0] [0 2 0] [0 0 3]] >>> print(label(x, connectivity=2)) [[1 0 0] [0 1 0] [0 0 1]] >>> print(label(x, background=-1)) [[1 2 2] [2 1 2] [2 2 1]] >>> x = np.array([[1, 0, 0], ... [1, 1, 5], ... [0, 0, 0]]) >>> print(label(x)) [[1 0 0] [1 1 2] [0 0 0]]
- skimage.measure.manders_coloc_coeff(image0, image1_mask, mask=None)[source]#
两个通道之间的 Manders 共定位系数。
- 参数:
- image0(M, N) ndarray
通道 A 的图像。所有像素值应为非负数。
- image1_mask(M, N) dtype 为 bool 的 ndarray
通道 B 中感兴趣区域的分割二值掩码。必须与
image0具有相同的维度。- mask(M, N) dtype 为 bool 的 ndarray,可选
计算中仅包含此感兴趣区域掩码内的
image0像素值。必须与image0具有相同的维度。
- 返回:
- mcc浮点数
Manders 共定位系数。
备注
Manders 共定位系数 (MCC) 是特定通道(通道 A)的总强度在第二个通道(通道 B)的分割区域内的部分 [1]。它的范围从 0(不共定位)到 1(完全共定位)。它也被称为 M1 和 M2。
MCC 通常用于测量特定蛋白质在亚细胞区室中的共定位。通常,通道 B 的分割掩码是通过设置阈值生成的,像素值必须高于该阈值才能包含在 MCC 计算中。在此实现中,通道 B 掩码作为参数
image1_mask提供,允许用户预先决定确切的分割方法。实现的公式为
\[r = \frac{\sum A_{i,coloc}}{\sum A_i}\]- 其中
\(A_i\) 是
image0中第 \(i^{th}\) 个像素的值,如果 \(Bmask_i > 0\),则 \(A_{i,coloc} = A_i\),\(Bmask_i\) 是mask中第 \(i^{th}\) 个像素的值。
MCC 对噪声敏感,第一个通道中的弥散信号会使其值膨胀。在计算 MCC 之前,应处理图像以去除散焦和背景光 [2]。
参考
[1]Manders, E.M.M., Verbeek, F.J. 和 Aten, J.A. (1993), Measurement of co-localization of objects in dual-colour confocal images. Journal of Microscopy, 169: 375-382. https://doi.org/10.1111/j.1365-2818.1993.tb03313.x https://imagej.net/media/manders.pdf
[2]Dunn, K. W., Kamocka, M. M., & McDonald, J. H. (2011). A practical guide to evaluating colocalization in biological microscopy. American journal of physiology. Cell physiology, 300(4), C723–C742. https://doi.org/10.1152/ajpcell.00462.2010
- skimage.measure.manders_overlap_coeff(image0, image1, mask=None)[source]#
曼德斯重叠系数
- 参数:
- image0(M, N) ndarray
通道 A 的图像。所有像素值应为非负数。
- image1(M, N) ndarray
通道 B 的图像。所有像素值应为非负数。必须与
image0具有相同的尺寸。- mask(M, N) dtype 为 bool 的 ndarray,可选
仅计算此感兴趣区域掩码内的
image0和image1像素值。必须与image0具有相同的尺寸。
- 返回:
- moc: float
两个图像之间像素强度的曼德斯重叠系数。
备注
曼德斯重叠系数 (MOC) 由以下公式给出 [1]
\[r = \frac{\sum A_i B_i}{\sqrt{\sum A_i^2 \sum B_i^2}}\]- 其中
\(A_i\) 是
image0中第 \(i^{th}\) 个像素的值,\(B_i\) 是image1中第 \(i^{th}\) 个像素的值。
它的范围在 0 到 1 之间,其中 0 表示没有共定位,1 表示所有像素完全共定位。
MOC 不考虑像素强度,仅考虑两个通道都具有正值的像素的比例 [R2208c1a5d6e1-2]_ [3]。它的有用性受到了批评,因为它会随着共现和相关性的差异而变化,因此特定的 MOC 值可能表示范围广泛的共定位模式 [4] [5]。
参考
[1]Manders, E.M.M., Verbeek, F.J. 和 Aten, J.A. (1993), Measurement of co-localization of objects in dual-colour confocal images. Journal of Microscopy, 169: 375-382. https://doi.org/10.1111/j.1365-2818.1993.tb03313.x https://imagej.net/media/manders.pdf
[2]Dunn, K. W., Kamocka, M. M., & McDonald, J. H. (2011). A practical guide to evaluating colocalization in biological microscopy. American journal of physiology. Cell physiology, 300(4), C723–C742. https://doi.org/10.1152/ajpcell.00462.2010
[3]Bolte, S. 和 Cordelières, F.P. (2006), A guided tour into subcellular colocalization analysis in light microscopy. Journal of Microscopy, 224: 213-232. https://doi.org/10.1111/j.1365-2818.2006.01
[4]Adler J, Parmryd I. (2010), Quantifying colocalization by correlation: the Pearson correlation coefficient is superior to the Mander’s overlap coefficient. Cytometry A. Aug;77(8):733-42.https://doi.org/10.1002/cyto.a.20896
[5]Adler, J, Parmryd, I. Quantifying colocalization: The case for discarding the Manders overlap coefficient. Cytometry. 2021; 99: 910– 920. https://doi.org/10.1002/cyto.a.24336
- skimage.measure.marching_cubes(volume, level=None, *, spacing=(1.0, 1.0, 1.0), gradient_direction='descent', step_size=1, allow_degenerate=True, method='lewiner', mask=None)[source]#
Marching Cubes 算法用于在 3D 体积数据中查找曲面。
与 Lorensen 等人的方法 [2] 相比,Lewiner 等人的算法速度更快,可以解决歧义,并保证拓扑正确的结果。因此,该算法通常是更好的选择。
- 参数:
- volume(M, N, P) ndarray
查找等值面的输入数据体积。如有必要,将在内部转换为 float32。
- levelfloat,可选
在
volume中搜索等值面的轮廓值。如果未给出或为 None,则使用 vol 的最小值和最大值的平均值。- spacing长度为 3 的浮点数元组,可选
空间维度中的体素间距,对应于 numpy 数组索引维度 (M, N, P),如
volume中所示。- gradient_direction字符串,可选
控制网格是从梯度下降到感兴趣对象的等值面生成的(默认),还是相反,考虑左手规则。两个选项为:* descent : 对象大于外部 * ascent : 外部大于对象
- step_sizeint,可选
以体素为单位的步长。默认值为 1。较大的步长会产生更快但更粗糙的结果。但结果始终在拓扑上正确。
- allow_degeneratebool,可选
是否允许最终结果中出现退化(即零面积)三角形。默认为 True。如果为 False,则会删除退化的三角形,但代价是使算法速度变慢。
- method: {‘lewiner’, ‘lorensen’}, 可选
是否使用 Lewiner 等人或 Lorensen 等人的方法。
- mask(M, N, P) 数组,可选
布尔数组。行进立方体算法仅在 True 元素上计算。当接口位于体积 M, N, P 的特定区域(例如立方体的上半部分)内时,这将节省计算时间,并且还允许计算有限的表面(即不在立方体边界处结束的开放表面)。
- 返回:
- verts(V, 3) 数组
V 个唯一网格顶点的空间坐标。坐标顺序与输入
volume(M, N, P) 匹配。如果allow_degenerate设置为 True,则网格中存在退化的三角形可能会使此数组具有重复的顶点。- faces(F, 3) 数组
通过引用
verts中的顶点索引来定义三角形面。此算法专门输出三角形,因此每个面都有三个索引。- normals(V, 3) 数组
每个顶点的法线方向,从数据中计算得出。
- values(V,) 数组
给出每个顶点附近局部区域中数据的最大值的度量。可视化工具可以使用它来对网格应用颜色映射。
备注
该算法 [1] 是 Chernyaev 的行进立方体 33 算法的改进版本。它是一种高效的算法,大量使用查找表来处理许多不同的情况,使算法相对简单。此实现是用 Cython 编写的,从 Lewiner 的 C++ 实现移植而来。
要量化此算法生成的等值面的面积,请将 verts 和 faces 传递给
skimage.measure.mesh_surface_area。关于算法输出的可视化,要使用
mayavi包绘制名为myvolume的体积中关于 0.0 水平面的轮廓>>> >> from mayavi import mlab >> verts, faces, _, _ = marching_cubes(myvolume, 0.0) >> mlab.triangular_mesh([vert[0] for vert in verts], [vert[1] for vert in verts], [vert[2] for vert in verts], faces) >> mlab.show()
类似地,使用
visvis包>>> >> import visvis as vv >> verts, faces, normals, values = marching_cubes(myvolume, 0.0) >> vv.mesh(np.fliplr(verts), faces, normals, values) >> vv.use().Run()
要减少网格中的三角形数量以获得更好的性能,请参阅使用
mayavi包的示例。参考
[1]Thomas Lewiner, Helio Lopes, Antonio Wilson Vieira 和 Geovan Tavares. Efficient implementation of Marching Cubes’ cases with topological guarantees. Journal of Graphics Tools 8(2) pp. 1-15 (december 2003). DOI:10.1080/10867651.2003.10487582
[2]Lorensen, William and Harvey E. Cline. Marching Cubes: A High Resolution 3D Surface Construction Algorithm. Computer Graphics (SIGGRAPH 87 Proceedings) 21(4) July 1987, p. 163-170). DOI:10.1145/37401.37422
- skimage.measure.mesh_surface_area(verts, faces)[source]#
计算给定顶点和三角形面的表面积。
- 参数:
- verts(V, 3) 浮点数数组
包含 V 个唯一网格顶点的坐标的数组。
- faces(F, 3) 整数数组
长度为 3 的整数列表,引用
verts中提供的顶点坐标。
- 返回:
- area浮点数
网格的表面积。单位现在是 [坐标单位] ** 2。
备注
此函数期望的参数是
skimage.measure.marching_cubes的前两个输出。对于单位正确的输出,请确保将正确的spacing传递给skimage.measure.marching_cubes。仅当提供的
faces全部为三角形时,此算法才能正常工作。
- skimage.measure.moments(image, order=3, *, spacing=None)[源代码]#
计算直到某个阶数的所有原始图像矩。
- 以下属性可以从原始图像矩计算得出
面积:
M[0, 0]。质心:{
M[1, 0] / M[0, 0],M[0, 1] / M[0, 0]}。
请注意,原始矩不具有平移、缩放或旋转不变性。
- 参数:
- image(N[, …]) 双精度或 uint8 数组
光栅化形状作为图像。
- orderint,可选
矩的最大阶数。默认值为 3。
- spacing: float 元组,形状 (ndim,)
图像沿每个轴的像素间距。
- 返回:
- m(
order + 1,order + 1) 数组 原始图像矩。
- m(
参考
[1]Wilhelm Burger, Mark Burge. 数字图像处理原理:核心算法。Springer-Verlag,伦敦,2009 年。
[2]B. Jähne。数字图像处理。Springer-Verlag,柏林-海德堡,第 6 版,2005 年。
[3]T. H. Reiss。使用不变图像特征识别平面物体,来自计算机科学讲义,第 676 页。Springer,柏林,1993 年。
示例
>>> image = np.zeros((20, 20), dtype=np.float64) >>> image[13:17, 13:17] = 1 >>> M = moments(image) >>> centroid = (M[1, 0] / M[0, 0], M[0, 1] / M[0, 0]) >>> centroid (14.5, 14.5)
- skimage.measure.moments_central(image, center=None, order=3, *, spacing=None, **kwargs)[源代码]#
计算直到某个阶数的所有中心图像矩。
中心坐标 (cr, cc) 可以从原始矩计算得出:{
M[1, 0] / M[0, 0],M[0, 1] / M[0, 0]}。请注意,中心矩具有平移不变性,但不具有缩放和旋转不变性。
- 参数:
- image(N[, …]) 双精度或 uint8 数组
光栅化形状作为图像。
- center浮点数元组,可选
图像质心的坐标。如果未提供,则将计算此值。
- orderint,可选
计算的矩的最大阶数。
- spacing: float 元组,形状 (ndim,)
图像沿每个轴的像素间距。
- 返回:
- mu(
order + 1,order + 1) 数组 中心图像矩。
- mu(
参考
[1]Wilhelm Burger, Mark Burge. 数字图像处理原理:核心算法。Springer-Verlag,伦敦,2009 年。
[2]B. Jähne。数字图像处理。Springer-Verlag,柏林-海德堡,第 6 版,2005 年。
[3]T. H. Reiss。使用不变图像特征识别平面物体,来自计算机科学讲义,第 676 页。Springer,柏林,1993 年。
示例
>>> image = np.zeros((20, 20), dtype=np.float64) >>> image[13:17, 13:17] = 1 >>> M = moments(image) >>> centroid = (M[1, 0] / M[0, 0], M[0, 1] / M[0, 0]) >>> moments_central(image, centroid) array([[16., 0., 20., 0.], [ 0., 0., 0., 0.], [20., 0., 25., 0.], [ 0., 0., 0., 0.]])
- skimage.measure.moments_coords(coords, order=3)[源代码]#
计算直到某个阶数的所有原始图像矩。
- 以下属性可以从原始图像矩计算得出
面积:
M[0, 0]。质心:{
M[1, 0] / M[0, 0],M[0, 1] / M[0, 0]}。
请注意,原始矩不具有平移、缩放或旋转不变性。
- 参数:
- coords(N, D) 双精度或 uint8 数组
描述笛卡尔空间中 D 维图像的 N 个点的数组。
- orderint,可选
矩的最大阶数。默认值为 3。
- 返回:
- M(
order + 1,order + 1, …) 数组 原始图像矩。(D 维度)
- M(
参考
[1]Johannes Kilian。基于矩的简单图像分析。达勒姆大学,0.2 版本,达勒姆,2001 年。
示例
>>> coords = np.array([[row, col] ... for row in range(13, 17) ... for col in range(14, 18)], dtype=np.float64) >>> M = moments_coords(coords) >>> centroid = (M[1, 0] / M[0, 0], M[0, 1] / M[0, 0]) >>> centroid (14.5, 15.5)
- skimage.measure.moments_coords_central(coords, center=None, order=3)[源代码]#
计算直到某个阶数的所有中心图像矩。
- 以下属性可以从原始图像矩计算得出
面积:
M[0, 0]。质心:{
M[1, 0] / M[0, 0],M[0, 1] / M[0, 0]}。
请注意,原始矩不具有平移、缩放或旋转不变性。
- 参数:
- coords(N, D) 双精度或 uint8 数组
描述笛卡尔空间中 D 维图像的 N 个点的数组。 也接受
np.nonzero返回的坐标元组作为输入。- center浮点数元组,可选
图像质心的坐标。如果未提供,则将计算此值。
- orderint,可选
矩的最大阶数。默认值为 3。
- 返回:
- Mc(
order + 1,order + 1, …) 数组 中心图像矩。(D 维度)
- Mc(
参考
[1]Johannes Kilian。基于矩的简单图像分析。达勒姆大学,0.2 版本,达勒姆,2001 年。
示例
>>> coords = np.array([[row, col] ... for row in range(13, 17) ... for col in range(14, 18)]) >>> moments_coords_central(coords) array([[16., 0., 20., 0.], [ 0., 0., 0., 0.], [20., 0., 25., 0.], [ 0., 0., 0., 0.]])
如上所述,对于对称对象,当以对象的质心或质量中心为中心时(默认设置),奇数阶矩(第 1 列和第 3 列,第 1 行和第 3 行)为零。 如果我们通过添加新点来打破对称性,则不再成立
>>> coords2 = np.concatenate((coords, [[17, 17]]), axis=0) >>> np.round(moments_coords_central(coords2), ... decimals=2) array([[17. , 0. , 22.12, -2.49], [ 0. , 3.53, 1.73, 7.4 ], [25.88, 6.02, 36.63, 8.83], [ 4.15, 19.17, 14.8 , 39.6 ]])
当中心为 (0, 0) 时,图像矩和中心图像矩是等效的(根据定义)
>>> np.allclose(moments_coords(coords), ... moments_coords_central(coords, (0, 0))) True
- skimage.measure.moments_hu(nu)[源代码]#
计算 Hu 的图像矩集(仅限 2D)。
请注意,已证明这组矩具有平移、缩放和旋转不变性。
- 参数:
- nu(M, M) 数组
归一化中心图像矩,其中 M 必须 >= 4。
- 返回:
- nu(7,) 数组
Hu 的图像矩集。
参考
[1]M. K. Hu,“通过矩不变量进行视觉模式识别”,IRE Trans. Info. Theory,卷。IT-8,第 179-187 页,1962 年
[2]Wilhelm Burger, Mark Burge. 数字图像处理原理:核心算法。Springer-Verlag,伦敦,2009 年。
[3]B. Jähne。数字图像处理。Springer-Verlag,柏林-海德堡,第 6 版,2005 年。
[4]T. H. Reiss。使用不变图像特征识别平面物体,来自计算机科学讲义,第 676 页。Springer,柏林,1993 年。
示例
>>> image = np.zeros((20, 20), dtype=np.float64) >>> image[13:17, 13:17] = 0.5 >>> image[10:12, 10:12] = 1 >>> mu = moments_central(image) >>> nu = moments_normalized(mu) >>> moments_hu(nu) array([0.74537037, 0.35116598, 0.10404918, 0.04064421, 0.00264312, 0.02408546, 0. ])
- skimage.measure.moments_normalized(mu, order=3, spacing=None)[源代码]#
计算直到某个阶数的所有归一化中心图像矩。
请注意,归一化中心矩具有平移和缩放不变性,但不具有旋转不变性。
- 参数:
- mu(M[, …], M) 数组
中心图像矩,其中 M 必须大于或等于
order。- orderint,可选
矩的最大阶数。默认值为 3。
- spacing: float 元组,形状 (ndim,)
图像沿每个轴的像素间距。
- 返回:
- nu(
order + 1``[, ...], ``order + 1) 数组 归一化中心图像矩。
- nu(
参考
[1]Wilhelm Burger, Mark Burge. 数字图像处理原理:核心算法。Springer-Verlag,伦敦,2009 年。
[2]B. Jähne。数字图像处理。Springer-Verlag,柏林-海德堡,第 6 版,2005 年。
[3]T. H. Reiss。使用不变图像特征识别平面物体,来自计算机科学讲义,第 676 页。Springer,柏林,1993 年。
示例
>>> image = np.zeros((20, 20), dtype=np.float64) >>> image[13:17, 13:17] = 1 >>> m = moments(image) >>> centroid = (m[0, 1] / m[0, 0], m[1, 0] / m[0, 0]) >>> mu = moments_central(image, centroid) >>> moments_normalized(mu) array([[ nan, nan, 0.078125 , 0. ], [ nan, 0. , 0. , 0. ], [0.078125 , 0. , 0.00610352, 0. ], [0. , 0. , 0. , 0. ]])
- skimage.measure.pearson_corr_coeff(image0, image1, mask=None)[源代码]#
计算通道中像素强度之间的皮尔逊相关系数。
- 参数:
- image0(M, N) ndarray
通道 A 的图像。
- image1(M, N) ndarray
要与通道 B 关联的通道 2 的图像。必须具有与
image0相同的尺寸。- mask(M, N) dtype 为 bool 的 ndarray,可选
只有
image0和image1中此感兴趣区域掩码内的像素才会包含在计算中。 必须具有与image0相同的尺寸。
- 返回:
- pcc浮点数
如果提供了掩码,则两幅图像之间像素强度的皮尔逊相关系数。
- p-value浮点数
双尾 p 值。
备注
皮尔逊相关系数 (PCC) 测量两幅图像像素强度之间的线性相关性。 其值范围为 -1(表示完全线性反相关)到 +1(表示完全线性相关)。p 值的计算假设每个输入图像中的像素强度呈正态分布。
使用了 Scipy 对皮尔逊相关系数的实现。 请参考它以获取更多信息和注意事项 [1]。
\[r = \frac{\sum (A_i - m_A_i) (B_i - m_B_i)} {\sqrt{\sum (A_i - m_A_i)^2 \sum (B_i - m_B_i)^2}}\]- 其中
\(A_i\) 是
image0中第 \(i^{th}\) 个像素的值,\(B_i\) 是image1中第 \(i^{th}\) 个像素的值,\(m_A_i\) 是image0中像素值的平均值,\(m_B_i\) 是image1中像素值的平均值。
较低的 PCC 值并不一定意味着两个通道强度之间没有相关性,只是表明没有线性相关性。如果您在视觉上识别出非线性相关性,您可能希望在 2D 散点图中绘制两个通道中每个通道的像素强度,并使用 Spearman 的秩相关性 [2]。此外,请考虑您感兴趣的是相关性还是共现性,在这种情况下,涉及分割掩码的方法(例如 MCC 或交集系数)可能更合适 [3] [4]。
提供图像中仅相关部分的掩码(例如,细胞或特定的细胞区室)并去除噪声非常重要,因为 PCC 对这些测量值很敏感 [3] [4]。
参考
[3] (1,2)Dunn, K. W., Kamocka, M. M., & McDonald, J. H. (2011). A practical guide to evaluating colocalization in biological microscopy. American journal of physiology. Cell physiology, 300(4), C723–C742. https://doi.org/10.1152/ajpcell.00462.2010
[4] (1,2)Bolte, S. and Cordelières, F.P. (2006), A guided tour into subcellular colocalization analysis in light microscopy. Journal of Microscopy, 224: 213-232. https://doi.org/10.1111/j.1365-2818.2006.01706.x
- skimage.measure.perimeter(image, neighborhood=4)[source]#
计算二值图像中所有对象的总周长。
- 参数:
- image(M, N) ndarray
二进制输入图像。
- neighborhood4 或 8,可选
用于边界像素确定的邻域连通性。它用于计算轮廓。较高的邻域会扩大计算周长的边界。
- 返回:
- perimeterfloat
二进制图像中所有对象的总周长。
参考
[1]K. Benkrid, D. Crookes. Design and FPGA Implementation of a Perimeter Estimator. The Queen’s University of Belfast. http://www.cs.qub.ac.uk/~d.crookes/webpubs/papers/perimeter.doc
示例
>>> from skimage import data, util >>> from skimage.measure import label >>> # coins image (binary) >>> img_coins = data.coins() > 110 >>> # total perimeter of all objects in the image >>> perimeter(img_coins, neighborhood=4) 7796.867... >>> perimeter(img_coins, neighborhood=8) 8806.268...
- skimage.measure.perimeter_crofton(image, directions=4)[source]#
计算二值图像中所有对象的总克罗夫顿周长。
- 参数:
- image(M, N) ndarray
输入图像。如果图像不是二值的,则所有大于零的值都视为对象。
- directions2 或 4,可选
用于近似 Crofton 周长的方向数。默认情况下使用 4:它应该比 2 更准确。两种情况下的计算时间相同。
- 返回:
- perimeterfloat
二进制图像中所有对象的总周长。
备注
此度量基于 Crofton 公式 [1],它是积分几何中的一个度量。它被定义为通过沿所有方向的双重积分来评估一般曲线长度。在离散空间中,2 个或 4 个方向可以给出很好的近似值,对于更复杂的形状,4 个方向比 2 个方向更准确。
与
perimeter()类似,此函数返回连续空间中周长的近似值。参考
[2]S. Rivollier. Analyse d’image geometrique et morphometrique par diagrammes de forme et voisinages adaptatifs generaux. PhD thesis, 2010. Ecole Nationale Superieure des Mines de Saint-Etienne. https://tel.archives-ouvertes.fr/tel-00560838
示例
>>> from skimage import data, util >>> from skimage.measure import label >>> # coins image (binary) >>> img_coins = data.coins() > 110 >>> # total perimeter of all objects in the image >>> perimeter_crofton(img_coins, directions=2) 8144.578... >>> perimeter_crofton(img_coins, directions=4) 7837.077...
- skimage.measure.points_in_poly(points, verts)[source]#
测试点是否位于多边形内。
- 参数:
- points(K, 2) 数组
输入点,
(x, y)。- verts(L, 2) 数组
多边形的顶点,按顺时针或逆时针排序。第一个点可以(但不需要)重复。
- 返回:
- mask(K,) 布尔数组
如果对应的点在多边形内,则为 True。
另请参阅
- skimage.measure.profile_line(image, src, dst, linewidth=1, order=None, mode='reflect', cval=0.0, *, reduce_func=<function mean>)[source]#
返回沿扫描线测量的图像的强度轮廓。
- 参数:
- imagendarray,形状 (M, N[, C])
图像,可以是灰度图像(2D 数组)或多通道图像(3D 数组,其中最后一个轴包含通道信息)。
- src类似数组,形状 (2,)
扫描线的起点坐标。
- dst类似数组,形状 (2,)
扫描线的终点坐标。与标准 numpy 索引相反,终点包含在轮廓中。
- linewidthint,可选
扫描宽度,垂直于线条
- orderint,取值 {0, 1, 2, 3, 4, 5},可选
样条插值的阶数,如果 image.dtype 是 bool,则默认为 0,否则为 1。该阶数必须在 0-5 的范围内。详情请参见
skimage.transform.warp。- mode{‘constant’, ‘nearest’, ‘reflect’, ‘mirror’, ‘wrap’},可选
如何计算落在图像外部的任何值。
- cvalfloat,可选
如果
mode为 ‘constant’,则在图像外部使用的常数值。- reduce_func可调用,可选
当
linewidth> 1 时,用于计算垂直于 profile_line 方向的像素值聚合的函数。如果设置为 None,则将返回未缩减的数组。
- 返回:
- return_value数组
沿扫描线的强度轮廓。轮廓的长度是扫描线计算长度的上限值。
示例
>>> x = np.array([[1, 1, 1, 2, 2, 2]]) >>> img = np.vstack([np.zeros_like(x), x, x, x, np.zeros_like(x)]) >>> img array([[0, 0, 0, 0, 0, 0], [1, 1, 1, 2, 2, 2], [1, 1, 1, 2, 2, 2], [1, 1, 1, 2, 2, 2], [0, 0, 0, 0, 0, 0]]) >>> profile_line(img, (2, 1), (2, 4)) array([1., 1., 2., 2.]) >>> profile_line(img, (1, 0), (1, 6), cval=4) array([1., 1., 1., 2., 2., 2., 2.])
与标准 numpy 索引相反,终点包含在轮廓中。例如
>>> profile_line(img, (1, 0), (1, 6)) # The final point is out of bounds array([1., 1., 1., 2., 2., 2., 2.]) >>> profile_line(img, (1, 0), (1, 5)) # This accesses the full first row array([1., 1., 1., 2., 2., 2.])
对于不同的 reduce_func 输入
>>> profile_line(img, (1, 0), (1, 3), linewidth=3, reduce_func=np.mean) array([0.66666667, 0.66666667, 0.66666667, 1.33333333]) >>> profile_line(img, (1, 0), (1, 3), linewidth=3, reduce_func=np.max) array([1, 1, 1, 2]) >>> profile_line(img, (1, 0), (1, 3), linewidth=3, reduce_func=np.sum) array([2, 2, 2, 4])
当
reduce_func为 None 或当reduce_func单独对每个像素值进行操作时,将返回未缩减的数组。>>> profile_line(img, (1, 2), (4, 2), linewidth=3, order=0, ... reduce_func=None) array([[1, 1, 2], [1, 1, 2], [1, 1, 2], [0, 0, 0]]) >>> profile_line(img, (1, 0), (1, 3), linewidth=3, reduce_func=np.sqrt) array([[1. , 1. , 0. ], [1. , 1. , 0. ], [1. , 1. , 0. ], [1.41421356, 1.41421356, 0. ]])
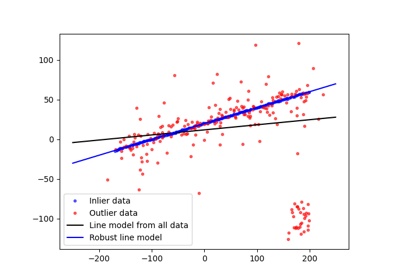
- skimage.measure.ransac(data, model_class, min_samples, residual_threshold, is_data_valid=None, is_model_valid=None, max_trials=100, stop_sample_num=inf, stop_residuals_sum=0, stop_probability=1, rng=None, initial_inliers=None)[source]#
使用 RANSAC(随机抽样一致)算法将模型拟合到数据。
RANSAC 是一种迭代算法,用于从完整数据集的内点子集中稳健地估计参数。每次迭代都会执行以下任务
从原始数据中选择
min_samples个随机样本,并检查数据集是否有效(请参见is_data_valid)。估计随机子集的模型 (
model_cls.estimate(*data[random_subset]) 并检查估计的模型是否有效(请参见is_model_valid)。通过计算残差来将所有数据分类为内点或外点(
model_cls.residuals(*data)) - 所有残差小于residual_threshold的数据样本都被认为是内点。如果内点样本数量最大,则将估计的模型保存为最佳模型。如果当前估计的模型具有相同数量的内点,则仅当其残差总和较小时才被视为最佳模型。
这些步骤会执行最大次数,或者直到满足某个特殊停止条件。最终模型是使用先前确定的最佳模型的所有内点样本进行估计的。
- 参数:
- data[list, tuple of] (N, …) 数组
用于拟合模型的数据集,其中 N 是数据点的数量,其余维度取决于模型的要求。如果模型类需要多个输入数据数组(例如,
skimage.transform.AffineTransform的源坐标和目标坐标),则可以选择将其作为元组或列表传递。请注意,在这种情况下,函数estimate(*data)、residuals(*data)、is_model_valid(model, *random_data)和is_data_valid(*random_data)都必须将每个数据数组作为单独的参数。- model_class对象
具有以下对象方法的对象
success = estimate(*data)residuals(*data)
- min_samples范围 (0, N) 内的整数
拟合模型所需的最小数据点数。
- residual_threshold大于 0 的浮点数
数据点被分类为内点的最大距离。
- is_data_valid函数,可选
此函数在将模型拟合到随机选择的数据之前被调用:
is_data_valid(*random_data)。- is_model_valid函数,可选
此函数使用估计的模型和随机选择的数据进行调用:
is_model_valid(model, *random_data)。- max_trials整数,可选
随机样本选择的最大迭代次数。
- stop_sample_num整数,可选
如果找到至少此数量的内点,则停止迭代。
- stop_residuals_sum浮点数,可选
如果残差之和小于或等于此阈值,则停止迭代。
- stop_probability范围 [0, 1] 内的浮点数,可选
如果至少一个无异常值的训练数据集的采样概率
probability >= stop_probability,则 RANSAC 迭代停止,这取决于当前最佳模型的内点比率和试验次数。这需要至少生成 N 个样本(试验)N >= log(1 - probability) / log(1 - e**m)
其中,概率(置信度)通常设置为较高的值(例如 0.99),e 是当前内点相对于总样本数的比例,m 是 min_samples 的值。
- rng{
numpy.random.Generator, int}, 可选 伪随机数生成器。默认情况下,使用 PCG64 生成器(请参阅
numpy.random.default_rng())。如果rng是一个整数,则它用于播种生成器。- initial_inliers类数组布尔值,形状 (N,),可选
用于模型估计的初始样本选择
- 返回:
- model对象
具有最大一致性集合的最佳模型。
- inliers(N,) 数组
分类为
True的内点的布尔掩码。
参考
[1]“RANSAC”,维基百科,https://en.wikipedia.org/wiki/RANSAC
示例
生成无倾斜的椭圆数据并添加噪声
>>> t = np.linspace(0, 2 * np.pi, 50) >>> xc, yc = 20, 30 >>> a, b = 5, 10 >>> x = xc + a * np.cos(t) >>> y = yc + b * np.sin(t) >>> data = np.column_stack([x, y]) >>> rng = np.random.default_rng(203560) # do not copy this value >>> data += rng.normal(size=data.shape)
添加一些错误数据
>>> data[0] = (100, 100) >>> data[1] = (110, 120) >>> data[2] = (120, 130) >>> data[3] = (140, 130)
使用所有可用数据估计椭圆模型
>>> model = EllipseModel() >>> model.estimate(data) True >>> np.round(model.params) array([ 72., 75., 77., 14., 1.])
使用 RANSAC 估计椭圆模型
>>> ransac_model, inliers = ransac(data, EllipseModel, 20, 3, max_trials=50) >>> abs(np.round(ransac_model.params)) array([20., 30., 10., 6., 2.]) >>> inliers array([False, False, False, False, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True], dtype=bool) >>> sum(inliers) > 40 True
RANSAC 可用于稳健地估计几何变换。在本节中,我们还将展示如何使用总样本的比例而不是绝对数量。
>>> from skimage.transform import SimilarityTransform >>> rng = np.random.default_rng() >>> src = 100 * rng.random((50, 2)) >>> model0 = SimilarityTransform(scale=0.5, rotation=1, ... translation=(10, 20)) >>> dst = model0(src) >>> dst[0] = (10000, 10000) >>> dst[1] = (-100, 100) >>> dst[2] = (50, 50) >>> ratio = 0.5 # use half of the samples >>> min_samples = int(ratio * len(src)) >>> model, inliers = ransac( ... (src, dst), ... SimilarityTransform, ... min_samples, ... 10, ... initial_inliers=np.ones(len(src), dtype=bool), ... ) >>> inliers array([False, False, False, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True])
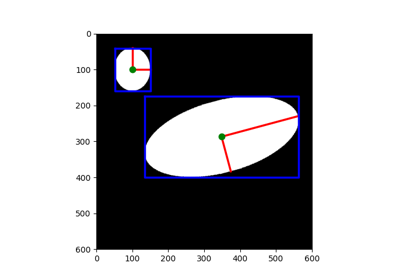
- skimage.measure.regionprops(label_image, intensity_image=None, cache=True, *, extra_properties=None, spacing=None, offset=None)[源代码]#
测量标记图像区域的属性。
- 参数:
- label_image(M, N[, P]) ndarray
标记的输入图像。忽略值为 0 的标签。
在版本 0.14.1 中更改:以前,
label_image由numpy.squeeze处理,因此允许任意数量的单例维度。这导致对具有单例维度的图像的处理不一致。要恢复旧的行为,请使用regionprops(np.squeeze(label_image), ...)。- intensity_image(M, N[, P][, C]) ndarray, 可选
强度(即,输入)图像,其大小与标记的图像相同,并且可以选择包含用于多通道数据的额外维度。目前,如果存在这个额外的通道维度,它必须是最后一个轴。默认为 None。
在版本 0.18.0 中更改:添加了为通道提供额外维度的功能。
- cachebool, 可选
确定是否缓存计算的属性。对于缓存的属性,计算速度快得多,而内存消耗会增加。
- extra_properties可迭代的调用对象
添加 skimage 未包含的额外属性计算函数。属性的名称派生自函数名称,数据类型通过在小样本上调用该函数来推断。如果额外属性的名称与现有属性的名称冲突,则该额外属性将不可见,并会发出 UserWarning。属性计算函数必须将区域掩码作为其第一个参数。如果属性需要强度图像,则必须接受强度图像作为第二个参数。
- spacing: float 元组,形状 (ndim,)
图像沿每个轴的像素间距。
- offset类数组整数,形状
(label_image.ndim,),可选 标签图像的原点(“左上角”)坐标。通常这是 ([0, ]0, 0),但如果想要获取较大体积中子体积的 regionprops,则可能有所不同。
- 返回:
- propertiesRegionProperties 列表
每个项目描述一个标记的区域,并且可以使用下面列出的属性进行访问。
另请参阅
备注
以下属性可以作为属性或键来访问
- area浮点数
区域的面积,即区域的像素数乘以像素面积。
- area_bbox浮点数
边界框的面积,即边界框的像素数乘以像素面积。
- area_convex浮点数
凸包图像的面积,它是包围该区域的最小凸多边形。
- area_filled浮点数
填充所有孔的区域面积。
- axis_major_length浮点数
具有与区域相同的归一化二阶中心矩的椭圆的长轴长度。
- axis_minor_length浮点数
具有与区域相同的归一化二阶中心矩的椭圆的短轴长度。
- bbox元组
边界框
(min_row, min_col, max_row, max_col)。属于边界框的像素位于半开区间[min_row; max_row)和[min_col; max_col)中。- centroid数组
质心坐标元组
(row, col)。- centroid_local数组
质心坐标元组
(row, col),相对于区域边界框。- centroid_weighted数组
使用强度图像加权的质心坐标元组
(row, col)。- centroid_weighted_local数组
相对于区域边界框,使用强度图像加权的质心坐标元组
(row, col)。- coords_scaled(K, 2) ndarray
按
spacing缩放的区域的坐标列表(row, col)。- coords(K, 2) ndarray
区域的坐标列表
(row, col)。- eccentricity浮点数
具有与该区域相同的二阶矩的椭圆的偏心率。偏心率是焦距(焦点之间的距离)与长轴长度的比率。该值在区间 [0, 1) 中。当它为 0 时,椭圆变为一个圆。
- equivalent_diameter_areafloat
与区域面积相同的圆的直径。
- euler_numberint
非零像素集合的欧拉特征。计算方式为连通分量的数量减去孔的数量(输入维度的连通性)。在 3D 中,计算方式为连通分量的数量加上孔的数量,再减去隧道数量。
- extentfloat
区域内像素与总边界框内像素的比率。计算方式为
area / (rows * cols)- feret_diameter_maxfloat
最大费雷直径,计算方式为区域凸包轮廓周围点之间的最长距离,由
find_contours确定。[5]- image(H, J) ndarray
切片的二值区域图像,其大小与边界框相同。
- image_convex(H, J) ndarray
二值凸包图像,其大小与边界框相同。
- image_filled(H, J) ndarray
填充孔的二值区域图像,其大小与边界框相同。
- image_intensityndarray
区域边界框内的图像。
- inertia_tensorndarray
区域绕其质心的旋转惯性张量。
- inertia_tensor_eigvalstuple
惯性张量的特征值,按降序排列。
- intensity_maxfloat
区域中具有最大强度的值。
- intensity_meanfloat
区域中平均强度的值。
- intensity_minfloat
区域中具有最小强度的值。
- intensity_stdfloat
区域中强度的标准差。
- labelint
在标记输入图像中的标签。
- moments(3, 3) ndarray
高达 3 阶的空间矩
m_ij = sum{ array(row, col) * row^i * col^j }
其中总和是对区域的
row和col坐标求和。- moments_central(3, 3) ndarray
高达 3 阶的中心矩(平移不变)
mu_ij = sum{ array(row, col) * (row - row_c)^i * (col - col_c)^j }
其中总和是对区域的
row和col坐标求和,row_c和col_c是区域质心的坐标。- moments_hutuple
Hu 矩(平移、尺度和旋转不变)。
- moments_normalized(3, 3) ndarray
高达 3 阶的归一化矩(平移和尺度不变)
nu_ij = mu_ij / m_00^[(i+j)/2 + 1]
其中
m_00是第零阶空间矩。- moments_weighted(3, 3) ndarray
高达 3 阶的强度图像的空间矩
wm_ij = sum{ array(row, col) * row^i * col^j }
其中总和是对区域的
row和col坐标求和。- moments_weighted_central(3, 3) ndarray
高达 3 阶的强度图像的中心矩(平移不变)
wmu_ij = sum{ array(row, col) * (row - row_c)^i * (col - col_c)^j }
其中总和是对区域的
row和col坐标求和,row_c和col_c是区域的加权质心的坐标。- moments_weighted_hutuple
强度图像的 Hu 矩(平移、尺度和旋转不变)。
- moments_weighted_normalized(3, 3) ndarray
高达 3 阶的强度图像的归一化矩(平移和尺度不变)
wnu_ij = wmu_ij / wm_00^[(i+j)/2 + 1]
其中
wm_00是第零阶空间矩(强度加权面积)。- num_pixelsint
前景像素的数量。
- orientationfloat
第 0 轴(行)与具有与区域相同二阶矩的椭圆的主轴之间的角度,范围从
-pi/2到pi/2,逆时针方向。- perimeterfloat
对象的周长,使用 4 连通性将轮廓近似为穿过边界像素中心的线。
- perimeter_croftonfloat
由 4 个方向的 Crofton 公式近似的对象周长。
- slicetuple of slices
从源图像中提取对象的切片。
- solidityfloat
区域中像素与凸包图像像素的比率。
每个区域还支持迭代,因此您可以执行
for prop in region: print(prop, region[prop])
参考
[1]Wilhelm Burger, Mark Burge. 数字图像处理原理:核心算法。Springer-Verlag,伦敦,2009 年。
[2]B. Jähne。数字图像处理。Springer-Verlag,柏林-海德堡,第 6 版,2005 年。
[3]T. H. Reiss。使用不变图像特征识别平面物体,来自计算机科学讲义,第 676 页。Springer,柏林,1993 年。
[5]W. Pabst, E. Gregorová. Characterization of particles and particle systems, pp. 27-28. ICT Prague, 2007. https://old.vscht.cz/sil/keramika/Characterization_of_particles/CPPS%20_English%20version_.pdf
示例
>>> from skimage import data, util >>> from skimage.measure import label, regionprops >>> img = util.img_as_ubyte(data.coins()) > 110 >>> label_img = label(img, connectivity=img.ndim) >>> props = regionprops(label_img) >>> # centroid of first labeled object >>> props[0].centroid (22.72987986048314, 81.91228523446583) >>> # centroid of first labeled object >>> props[0]['centroid'] (22.72987986048314, 81.91228523446583)
通过传递函数作为
extra_properties添加自定义测量值>>> from skimage import data, util >>> from skimage.measure import label, regionprops >>> import numpy as np >>> img = util.img_as_ubyte(data.coins()) > 110 >>> label_img = label(img, connectivity=img.ndim) >>> def pixelcount(regionmask): ... return np.sum(regionmask) >>> props = regionprops(label_img, extra_properties=(pixelcount,)) >>> props[0].pixelcount 7741 >>> props[1]['pixelcount'] 42
- skimage.measure.regionprops_table(label_image, intensity_image=None, properties=('label', 'bbox'), *, cache=True, separator='-', extra_properties=None, spacing=None)[source]#
计算图像属性并将其作为与 pandas 兼容的表格返回。
该表是一个字典,将列名映射到值数组。有关详细信息,请参阅下面的“注释”部分。
在 0.16 版本中添加。
- 参数:
- label_image(M, N[, P]) ndarray
标记的输入图像。忽略值为 0 的标签。
- intensity_image(M, N[, P][, C]) ndarray, 可选
强度(即输入)图像,其大小与标记图像相同,并且可以选择为多通道数据添加额外的维度。如果存在通道维度,则该维度必须是最后一个轴。默认为 None。
在版本 0.18.0 中更改:添加了为通道提供额外维度的功能。
- propertiestuple 或 list of str,可选
将包含在结果字典中的属性。有关可用属性列表,请参阅
regionprops()。用户应记住添加“label”以跟踪区域标识。- cachebool, 可选
确定是否缓存计算的属性。对于缓存的属性,计算速度快得多,而内存消耗会增加。
- separatorstr,可选
对于未在 OBJECT_COLUMNS 中列出的非标量属性,每个元素将出现在其自己的列中,该元素的索引与属性名称之间由该分隔符分隔。例如,2D 区域的惯性张量将出现在四列中:
inertia_tensor-0-0、inertia_tensor-0-1、inertia_tensor-1-0和inertia_tensor-1-1(其中分隔符为-)。对象列是指无法以这种方式拆分的列,因为列的数量会根据对象而变化。例如,
image和coords。- extra_properties可迭代的调用对象
添加 skimage 未包含的额外属性计算函数。属性的名称派生自函数名称,数据类型通过在小样本上调用该函数来推断。如果额外属性的名称与现有属性的名称冲突,则该额外属性将不可见,并会发出 UserWarning。属性计算函数必须将区域掩码作为其第一个参数。如果属性需要强度图像,则必须接受强度图像作为第二个参数。
- spacing: float 元组,形状 (ndim,)
图像沿每个轴的像素间距。
- 返回:
- out_dictdict
字典,将属性名称映射到该属性的值数组,每个区域一个值。此字典可用作 pandas
DataFrame的输入,以将属性名称映射到框架中的列,并将区域映射到行。如果图像没有区域,则数组的长度为 0,但类型正确。
备注
每一列都包含一个标量属性、一个对象属性或多维数组中的一个元素。
每个区域具有标量值的属性,如“eccentricity”,将显示为浮点数或整数数组,并以该属性名称作为键。
对于给定图像维度大小固定的多维属性,如“centroid”(在 3D 图像中,无论区域大小如何,每个质心都有三个元素),将被拆分为多个列,其名称为 {property_name}{separator}{element_num}(对于 1D 属性),{property_name}{separator}{elem_num0}{separator}{elem_num1}(对于 2D 属性),等等。
对于没有固定大小的多维属性,如“image”(区域的图像大小因区域大小而异),将使用对象数组,并以相应的属性名称作为键。
示例
>>> from skimage import data, util, measure >>> image = data.coins() >>> label_image = measure.label(image > 110, connectivity=image.ndim) >>> props = measure.regionprops_table(label_image, image, ... properties=['label', 'inertia_tensor', ... 'inertia_tensor_eigvals']) >>> props {'label': array([ 1, 2, ...]), ... 'inertia_tensor-0-0': array([ 4.012...e+03, 8.51..., ...]), ... ..., 'inertia_tensor_eigvals-1': array([ 2.67...e+02, 2.83..., ...])}
如果已安装 pandas,则可以将生成的字典直接传递给 pandas 以获得干净的 DataFrame
>>> import pandas as pd >>> data = pd.DataFrame(props) >>> data.head() label inertia_tensor-0-0 ... inertia_tensor_eigvals-1 0 1 4012.909888 ... 267.065503 1 2 8.514739 ... 2.834806 2 3 0.666667 ... 0.000000 3 4 0.000000 ... 0.000000 4 5 0.222222 ... 0.111111
[5 行 x 7 列]
如果我们想要测量一个非内置属性的功能,我们可以定义自定义函数并将它们作为
extra_properties传递。例如,我们可以创建一个自定义函数来测量区域中的强度四分位数>>> from skimage import data, util, measure >>> import numpy as np >>> def quartiles(regionmask, intensity): ... return np.percentile(intensity[regionmask], q=(25, 50, 75)) >>> >>> image = data.coins() >>> label_image = measure.label(image > 110, connectivity=image.ndim) >>> props = measure.regionprops_table(label_image, intensity_image=image, ... properties=('label',), ... extra_properties=(quartiles,)) >>> import pandas as pd >>> pd.DataFrame(props).head() label quartiles-0 quartiles-1 quartiles-2 0 1 117.00 123.0 130.0 1 2 111.25 112.0 114.0 2 3 111.00 111.0 111.0 3 4 111.00 111.5 112.5 4 5 112.50 113.0 114.0
- skimage.measure.shannon_entropy(image, base=2)[source]#
计算图像的香农熵。
香农熵定义为 S = -sum(pk * log(pk)),其中 pk 是值 k 的像素的频率/概率。
- 参数:
- image(M, N) ndarray
灰度输入图像。
- basefloat,可选
要使用的对数底数。
- 返回:
- entropyfloat
备注
对于 base=2,返回的值以比特或香农 (Sh) 为单位进行测量;对于 base=np.e,以自然单位 (nat) 为单位进行测量;对于 base=10,以哈特利 (Hart) 为单位进行测量。
参考
示例
>>> from skimage import data >>> from skimage.measure import shannon_entropy >>> shannon_entropy(data.camera()) 7.231695011055706
- skimage.measure.subdivide_polygon(coords, degree=2, preserve_ends=False)[source]#
使用 B 样条细分多边形曲线。
请注意,生成的曲线始终位于原始多边形的凸包内。圆形多边形在细分后保持闭合状态。
- 参数:
- coords(K, 2) 数组
坐标数组。
- degree{1, 2, 3, 4, 5, 6, 7},可选
B 样条的度数。默认为 2。
- preserve_endsbool, 可选
保留非圆形多边形的第一个和最后一个坐标。默认为 False。
- 返回:
- coords(L, 2) 数组
细分后的坐标数组。
参考
- class skimage.measure.CircleModel[源代码]#
基类:
BaseModel二维圆的总最小二乘估计器。
圆的函数模型为
r**2 = (x - xc)**2 + (y - yc)**2
此估计器最小化所有点到圆的平方距离
min{ sum((r - sqrt((x_i - xc)**2 + (y_i - yc)**2))**2) }
至少需要 3 个点才能求解参数。
- 属性:
- paramstuple
圆模型参数,按以下顺序排列
xc,yc,r。
备注
该估计使用 [1] 中给出的球形估计的 2D 版本进行。
参考
[1]Jekel, Charles F. 通过逆气泡膨胀获取聚氯乙烯涂层聚酯的非线性正交各向异性材料模型。论文(工程硕士),斯泰伦博斯大学,2016 年。附录 A,第 83-87 页。https://hdl.handle.net/10019.1/98627
示例
>>> t = np.linspace(0, 2 * np.pi, 25) >>> xy = CircleModel().predict_xy(t, params=(2, 3, 4)) >>> model = CircleModel() >>> model.estimate(xy) True >>> tuple(np.round(model.params, 5)) (2.0, 3.0, 4.0) >>> res = model.residuals(xy) >>> np.abs(np.round(res, 9)) array([0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.])
- estimate(data)[源代码]#
使用总体最小二乘法从数据中估计圆模型。
- 参数:
- data(N, 2) 数组
N 个点,分别具有
(x, y)坐标。
- 返回:
- successbool
如果模型估计成功,则为 True。
- class skimage.measure.EllipseModel[源代码]#
基类:
BaseModel二维椭圆的总最小二乘估计器。
椭圆的函数模型为
xt = xc + a*cos(theta)*cos(t) - b*sin(theta)*sin(t) yt = yc + a*sin(theta)*cos(t) + b*cos(theta)*sin(t) d = sqrt((x - xt)**2 + (y - yt)**2)
其中
(xt, yt)是椭圆上最接近(x, y)的点。因此 d 是从点到椭圆的最短距离。该估计器基于最小二乘法最小化。直接计算最优解,无需迭代。这导致了一种简单、稳定和鲁棒的拟合方法。
params属性包含以下顺序的参数xc, yc, a, b, theta
- 属性:
- paramstuple
椭圆模型参数,按以下顺序排列
xc,yc,a,b,theta。
示例
>>> xy = EllipseModel().predict_xy(np.linspace(0, 2 * np.pi, 25), ... params=(10, 15, 8, 4, np.deg2rad(30))) >>> ellipse = EllipseModel() >>> ellipse.estimate(xy) True >>> np.round(ellipse.params, 2) array([10. , 15. , 8. , 4. , 0.52]) >>> np.round(abs(ellipse.residuals(xy)), 5) array([0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.])
- estimate(data)[源代码]#
使用总体最小二乘法从数据中估计椭圆模型。
- 参数:
- data(N, 2) 数组
N 个点,分别具有
(x, y)坐标。
- 返回:
- successbool
如果模型估计成功,则为 True。
参考
[1]Halir, R.; Flusser, J. “椭圆的数值稳定直接最小二乘拟合”。在第六届中欧计算机图形与可视化国际会议论文集。WSCG(第 98 卷,第 125-132 页)。
- class skimage.measure.LineModelND[源代码]#
基类:
BaseModelN 维直线的总最小二乘估计器。
与普通最小二乘线估计相反,此估计器最小化点到估计线的正交距离。
线由一个点(原点)和一个单位向量(方向)根据以下向量方程定义
X = origin + lambda * direction
- 属性:
- paramstuple
线模型参数,按以下顺序排列
origin,direction。
示例
>>> x = np.linspace(1, 2, 25) >>> y = 1.5 * x + 3 >>> lm = LineModelND() >>> lm.estimate(np.stack([x, y], axis=-1)) True >>> tuple(np.round(lm.params, 5)) (array([1.5 , 5.25]), array([0.5547 , 0.83205])) >>> res = lm.residuals(np.stack([x, y], axis=-1)) >>> np.abs(np.round(res, 9)) array([0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.]) >>> np.round(lm.predict_y(x[:5]), 3) array([4.5 , 4.562, 4.625, 4.688, 4.75 ]) >>> np.round(lm.predict_x(y[:5]), 3) array([1. , 1.042, 1.083, 1.125, 1.167])
- estimate(data)[源代码]#
从数据估计线模型。
这最小化了给定数据点到估计线的最小(正交)距离之和。
- 参数:
- data(N, dim) 数组
维度 dim >= 2 的空间中的 N 个点。
- 返回:
- successbool
如果模型估计成功,则为 True。
- predict(x, axis=0, params=None)[源代码]#
预测估计的线模型与垂直于给定轴的超平面的交点。
- 参数:
- x(n, 1) 数组
沿轴的坐标。
- axisint
与与直线相交的超平面垂直的轴。
- params(2,) 数组,可选
可选的自定义参数集,格式为 (
origin,direction)。
- 返回:
- data(n, m) 数组
预测的坐标。
- 引发:
- ValueError
如果线平行于给定的轴。
- predict_x(y, params=None)[源代码]#
使用估计的模型预测 2D 线的 x 坐标。
别名为
predict(y, axis=1)[:, 0]
- 参数:
- y数组
y 坐标。
- params(2,) 数组,可选
可选的自定义参数集,格式为 (
origin,direction)。
- 返回:
- x数组
预测的 x 坐标。