skimage.segmentation#
将图像分割成有意义的区域或边界的算法。
主动轮廓模型。 |
|
Chan-Vese 分割算法。 |
|
使用二进制值创建棋盘格水平集。 |
|
清除连接到标签图像边界的对象。 |
|
使用二进制值创建圆形水平集。 |
|
在标签图像中按 |
|
计算 Felsenszwalb 的高效基于图的图像分割。 |
|
返回布尔数组,其中标记区域之间的边界为 True。 |
|
与洪水填充相对应的掩码。 |
|
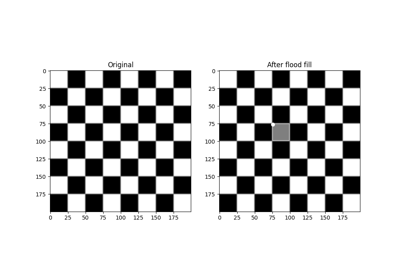
在图像上执行洪水填充。 |
|
梯度大小的倒数。 |
|
返回两个输入分割的连接。 |
|
返回突出显示标记区域之间边界的图像。 |
|
无边缘的形态学主动轮廓(MorphACWE) |
|
形态学测地线主动轮廓(MorphGAC)。 |
|
在颜色-(x,y)空间中使用快速移位聚类分割图像。 |
|
用于从标记进行分割的随机游走算法。 |
|
将任意标签重新标记为 { |
|
在颜色-(x,y,z)空间中使用 k-means 聚类分割图像。 |
|
在从给定标记填充的图像中查找分水岭盆地。 |
- skimage.segmentation.active_contour(image, snake, alpha=0.01, beta=0.1, w_line=0, w_edge=1, gamma=0.01, max_px_move=1.0, max_num_iter=2500, convergence=0.1, *, boundary_condition='periodic')[源代码]#
主动轮廓模型。
通过将蛇拟合到图像的特征来获得主动轮廓。支持单通道和多通道 2D 图像。蛇可以是周期性的(用于分割)或具有固定和/或自由端。输出蛇的长度与输入边界相同。由于点的数量是恒定的,请确保初始蛇有足够的点来捕获最终轮廓的细节。
- 参数:
- image(M, N) 或 (M, N, 3) ndarray
输入图像。
- snake(K, 2) ndarray
初始蛇坐标。对于周期性边界条件,端点不得重复。
- alphafloat,可选
蛇长度形状参数。较高的值会使蛇收缩得更快。
- betafloat,可选
蛇平滑度形状参数。较高的值会使蛇更平滑。
- w_linefloat,可选
控制对亮度的吸引力。使用负值吸引朝向黑暗区域。
- w_edgefloat,可选
控制对边缘的吸引力。使用负值将蛇从边缘排斥出去。
- gammafloat,可选
显式时间步进参数。
- max_px_movefloat,可选
每次迭代移动的最大像素距离。
- max_num_iterint,可选
优化蛇形的最大迭代次数。
- convergencefloat,可选
收敛标准。
- boundary_conditionstring,可选
轮廓的边界条件。可以是 'periodic'、'free'、'fixed'、'free-fixed' 或 'fixed-free' 之一。'periodic' 连接蛇的两端,'fixed' 将端点固定到位,'free' 允许端的自由移动。'fixed' 和 'free' 可以通过解析 'fixed-free'、'free-fixed' 来组合。解析 'fixed-fixed' 或 'free-free' 会产生与 'fixed' 和 'free' 分别相同的行为。
- 返回:
- snake(K, 2) ndarray
优化的蛇,与输入参数的形状相同。
参考
[1]Kass, M.; Witkin, A.; Terzopoulos, D. “Snakes: Active contour models”. International Journal of Computer Vision 1 (4): 321 (1988). DOI:10.1007/BF00133570
示例
>>> from skimage.draw import circle_perimeter >>> from skimage.filters import gaussian
创建并平滑图像
>>> img = np.zeros((100, 100)) >>> rr, cc = circle_perimeter(35, 45, 25) >>> img[rr, cc] = 1 >>> img = gaussian(img, sigma=2, preserve_range=False)
初始化样条
>>> s = np.linspace(0, 2*np.pi, 100) >>> init = 50 * np.array([np.sin(s), np.cos(s)]).T + 50
将样条拟合到图像
>>> snake = active_contour(img, init, w_edge=0, w_line=1) >>> dist = np.sqrt((45-snake[:, 0])**2 + (35-snake[:, 1])**2) >>> int(np.mean(dist)) 25
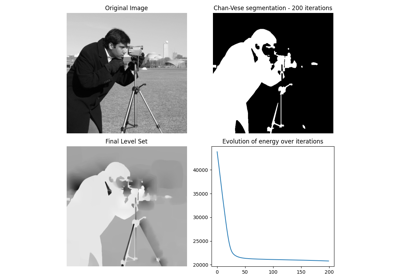
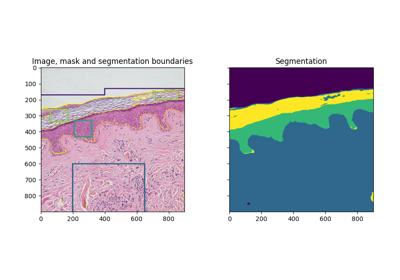
- skimage.segmentation.chan_vese(image, mu=0.25, lambda1=1.0, lambda2=1.0, tol=0.001, max_num_iter=500, dt=0.5, init_level_set='checkerboard', extended_output=False)[源代码]#
Chan-Vese 分割算法。
通过演化水平集的主动轮廓模型。可用于分割没有明确定义的边界的对象。
- 参数:
- image(M, N) ndarray
要分割的灰度图像。
- mufloat,可选
“边缘长度”权重参数。较高的
mu值将产生“圆形”边缘,而接近于零的值将检测较小的对象。- lambda1float,可选
值“True”的输出区域的“与平均值的差异”权重参数。如果它低于
lambda2,则此区域的值范围将大于另一个区域。- lambda2float,可选
值“False”的输出区域的“与平均值的差异”权重参数。如果它低于
lambda1,则此区域的值范围将大于另一个区域。- tolfloat,正值,可选
迭代之间水平集变化的容差。如果连续迭代的水平集的 L2 范数差异除以图像的面积低于此值,则该算法将假定已达到解。
- max_num_iteruint,可选
算法中断自身之前允许的最大迭代次数。
- dtfloat,可选
在每个步骤的计算中应用的乘法因子,用于加速算法。虽然较高的值可能会加快算法的速度,但它们也可能导致收敛问题。
- init_level_setstr 或 (M, N) ndarray,可选
定义算法使用的起始水平集。如果输入的是字符串,则会自动生成与图像大小匹配的水平集。或者,可以定义自定义水平集,它应该是一个浮点数值数组,形状与“图像”相同。接受的字符串值如下。
- ‘棋盘格’
起始水平集定义为 sin(x/5*pi)*sin(y/5*pi),其中 x 和 y 是像素坐标。此水平集收敛速度快,但可能无法检测到隐式边缘。
- ‘圆盘’
起始水平集定义为图像中心到像素的距离的相反数,再减去图像宽度和高度之间最小值的一半。这种方式速度较慢,但更可能正确检测到隐式边缘。
- ‘小圆盘’
起始水平集定义为图像中心到像素的距离的相反数,再减去图像宽度和高度之间最小值的四分之一。
- extended_outputbool,可选
如果设置为 True,则返回值将是一个包含三个返回值的元组(见下文)。如果设置为 False(默认值),则仅返回“分割”数组。
- 返回:
- 分割(M, N) ndarray,bool
算法产生的分割结果。
- phi(M, N) 浮点数ndarray
算法计算的最终水平集。
- 能量浮点数列表
显示算法每一步的“能量”变化。这应该可以用来检查算法是否收敛。
注释
Chan-Vese 算法旨在分割没有明确边界的对象。此算法基于迭代演化的水平集,以最小化能量。能量由加权值定义,这些加权值对应于分割区域外部的平均强度差异之和、分割区域内部的平均强度差异之和,以及一个与分割区域边界长度相关的项。
此算法最初由 Tony Chan 和 Luminita Vese 在一篇题为“An Active Contour Model Without Edges”的出版物中提出[1]。
此算法的实现方式有些简化,因为原始论文中描述的面积因子“nu”未实现,并且仅适用于灰度图像。
lambda1和lambda2的典型值为 1。如果“背景”在分布方面与分割的对象有很大差异(例如,具有不同强度图形的均匀黑色图像),则这些值应彼此不同。mu 的典型值介于 0 和 1 之间,但处理轮廓非常不清晰的形状时可以使用更高的值。
此算法尝试最小化的“能量”定义为区域内平均值之差的平方和,并乘以“lambda”因子,再加上轮廓长度乘以“mu”因子。
仅支持 2D 灰度图像,并且未实现原始文章中描述的面积项。
参考
[1]An Active Contour Model without Edges, Tony Chan and Luminita Vese, Scale-Space Theories in Computer Vision, 1999, DOI:10.1007/3-540-48236-9_13
[2]Chan-Vese Segmentation, Pascal Getreuer Image Processing On Line, 2 (2012), pp. 214-224, DOI:10.5201/ipol.2012.g-cv
[3]The Chan-Vese Algorithm - Project Report, Rami Cohen, 2011 arXiv:1107.2782
- skimage.segmentation.checkerboard_level_set(image_shape, square_size=5)[source]#
使用二进制值创建棋盘格水平集。
- 参数:
- image_shape正整数元组
图像的形状。
- square_sizeint,可选
棋盘格的方块大小。默认为 5。
- 返回:
- out形状为
image_shape的数组 棋盘格的二元水平集。
- out形状为
另请参阅
- skimage.segmentation.clear_border(labels, buffer_size=0, bgval=0, mask=None, *, out=None)[source]#
清除连接到标签图像边界的对象。
- 参数:
- labels(M[, N[, …, P]]) 整数或布尔数组
图像数据标签。
- buffer_sizeint,可选
检查的边界宽度。默认情况下,仅删除接触图像外部的对象。
- bgvalfloat 或 int,可选
清除的对象设置为此值。
- mask与
image形状相同的布尔ndarray,可选。 图像数据掩码。 labels 图像中与 mask 的 False 像素重叠的对象将被删除。如果定义,则将忽略参数 buffer_size。
- outndarray
与
labels形状相同的数组,输出放置到其中。默认情况下,将创建一个新数组。
- 返回:
- out(M[, N[, …, P]]) 数组
具有清除边界的图像数据标签
示例
>>> import numpy as np >>> from skimage.segmentation import clear_border >>> labels = np.array([[0, 0, 0, 0, 0, 0, 0, 1, 0], ... [1, 1, 0, 0, 1, 0, 0, 1, 0], ... [1, 1, 0, 1, 0, 1, 0, 0, 0], ... [0, 0, 0, 1, 1, 1, 1, 0, 0], ... [0, 1, 1, 1, 1, 1, 1, 1, 0], ... [0, 0, 0, 0, 0, 0, 0, 0, 0]]) >>> clear_border(labels) array([[0, 0, 0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 1, 0, 0, 0, 0], [0, 0, 0, 1, 0, 1, 0, 0, 0], [0, 0, 0, 1, 1, 1, 1, 0, 0], [0, 1, 1, 1, 1, 1, 1, 1, 0], [0, 0, 0, 0, 0, 0, 0, 0, 0]]) >>> mask = np.array([[0, 0, 1, 1, 1, 1, 1, 1, 1], ... [0, 0, 1, 1, 1, 1, 1, 1, 1], ... [1, 1, 1, 1, 1, 1, 1, 1, 1], ... [1, 1, 1, 1, 1, 1, 1, 1, 1], ... [1, 1, 1, 1, 1, 1, 1, 1, 1], ... [1, 1, 1, 1, 1, 1, 1, 1, 1]]).astype(bool) >>> clear_border(labels, mask=mask) array([[0, 0, 0, 0, 0, 0, 0, 1, 0], [0, 0, 0, 0, 1, 0, 0, 1, 0], [0, 0, 0, 1, 0, 1, 0, 0, 0], [0, 0, 0, 1, 1, 1, 1, 0, 0], [0, 1, 1, 1, 1, 1, 1, 1, 0], [0, 0, 0, 0, 0, 0, 0, 0, 0]])
- skimage.segmentation.disk_level_set(image_shape, *, center=None, radius=None)[source]#
使用二进制值创建圆形水平集。
- 参数:
- image_shape正整数元组
图像的形状
- center正整数元组,可选
圆盘中心的坐标,以 (行,列) 给出。如果未给出,则默认为图像的中心。
- radiusfloat,可选
圆盘的半径。如果未给出,则设置为最小图像尺寸的 75%。
- 返回:
- out形状为
image_shape的数组 具有给定
radius和center的圆盘的二元水平集。
- out形状为
- skimage.segmentation.expand_labels(label_image, distance=1, spacing=1)[source]#
在标签图像中按
distance像素扩展标签,不重叠。给定一个标签图像,
expand_labels将标签区域(连通分量)向外扩展,最大可扩展distance个单位,而不会溢出到相邻区域。更具体地说,在连通分量欧几里得距离 <=distance个像素范围内的每个背景像素都会分配该连通分量的标签。spacing参数可用于指定距离变换的间距速率,该间距变换用于计算各向异性图像的欧几里得距离。当多个连通分量在背景像素的distance个像素范围内时,将分配最接近的连通分量的标签值(有关等距离多个标签的情况,请参阅“注释”)。- 参数:
- label_imagedtype 为 int 的 ndarray
标签图像
- distancefloat
以像素为单位扩展标签的欧几里得距离。默认为 1。
- spacingfloat 或 float 序列,可选
沿每个维度的元素间距。如果是一个序列,则其长度必须等于输入秩;如果是一个数字,则将其用于所有轴。如果未指定,则表示单位网格间距。
- 返回:
- enlarged_labelsdtype 为 int 的 ndarray
标记的数组,其中所有连通区域都已扩大
注释
如果标签间隔大于
distance个像素,则这等效于使用半径为distance的圆盘或超球进行形态学膨胀。但是,与形态学膨胀相比,expand_labels不会将标签区域扩展到相邻区域。此
expand_labels的实现源自 CellProfiler [1],在 CellProfiler 中,它被称为模块“IdentifySecondaryObjects (Distance-N)” [2]。当一个像素到多个区域的距离相同时,会出现一个重要的边界情况,因为没有定义哪个区域会扩展到该空间。这里,确切的行为取决于上游
scipy.ndimage.distance_transform_edt的实现。参考
示例
>>> labels = np.array([0, 1, 0, 0, 0, 0, 2]) >>> expand_labels(labels, distance=1) array([1, 1, 1, 0, 0, 2, 2])
标签不会相互覆盖
>>> expand_labels(labels, distance=3) array([1, 1, 1, 1, 2, 2, 2])
如果出现距离相等的情况,行为是未定义的,但目前会解析为按字典顺序最接近
(0,) * ndim的标签。>>> labels_tied = np.array([0, 1, 0, 2, 0]) >>> expand_labels(labels_tied, 1) array([1, 1, 1, 2, 2]) >>> labels2d = np.array( ... [[0, 1, 0, 0], ... [2, 0, 0, 0], ... [0, 3, 0, 0]] ... ) >>> expand_labels(labels2d, 1) array([[2, 1, 1, 0], [2, 2, 0, 0], [2, 3, 3, 0]]) >>> expand_labels(labels2d, 1, spacing=[1, 0.5]) array([[1, 1, 1, 1], [2, 2, 2, 0], [3, 3, 3, 3]])
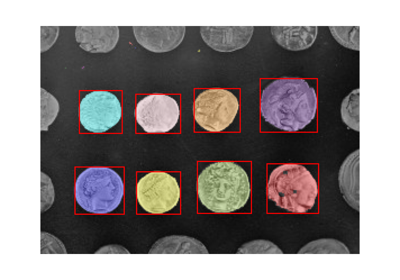
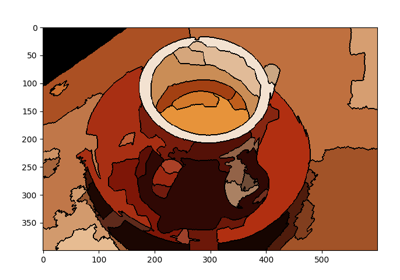
- skimage.segmentation.felzenszwalb(image, scale=1, sigma=0.8, min_size=20, *, channel_axis=-1)[source]#
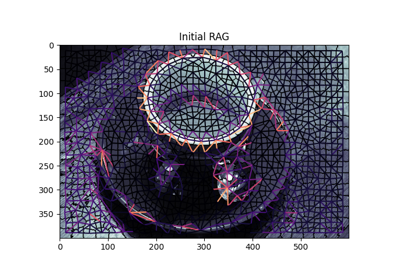
计算 Felsenszwalb 的高效基于图的图像分割。
使用快速、基于最小生成树的图像网格聚类,对多通道(即 RGB)图像进行过分割。参数
scale设置观察级别。较高的 scale 值意味着更少更大的分割区域。sigma是高斯核的直径,用于在分割之前平滑图像。生成的分割区域的数量及其大小只能通过
scale间接控制。图像内的分割区域大小可能因局部对比度而有很大差异。对于 RGB 图像,该算法使用颜色空间中像素之间的欧几里得距离。
- 参数:
- image(M, N[, 3]) ndarray
输入图像。
- scalefloat
自由参数。值越高,聚类越大。
- sigmafloat
预处理中使用的高斯核的宽度(标准差)。
- min_sizeint
最小组件大小。使用后处理强制执行。
- channel_axisint 或 None,可选
如果为 None,则假定图像为灰度(单通道)图像。否则,此参数指示数组的哪个轴对应于通道。
0.19 版本新增:
channel_axis在 0.19 版本中添加。
- 返回:
- segment_mask(M, N) ndarray
整数掩码,指示分割标签。
注释
原始论文中使用的
k参数在此处重命名为scale。参考
[1]高效的基于图的图像分割,Felzenszwalb, P.F. 和 Huttenlocher, D.P. 计算机视觉国际期刊,2004
示例
>>> from skimage.segmentation import felzenszwalb >>> from skimage.data import coffee >>> img = coffee() >>> segments = felzenszwalb(img, scale=3.0, sigma=0.95, min_size=5)
- skimage.segmentation.find_boundaries(label_img, connectivity=1, mode='thick', background=0)[source]#
返回布尔数组,其中标记区域之间的边界为 True。
- 参数:
- label_img整数或布尔值的数组
一个数组,其中不同的区域用不同的整数或布尔值标记。
- connectivity整数,取值范围为 {1, …,
label_img.ndim},可选 如果一个像素的任何邻居具有不同的标签,则该像素被视为边界像素。
connectivity控制哪些像素被视为邻居。连通性为 1(默认)表示共享边(在 2D 中)或面(在 3D 中)的像素将被视为邻居。连通性为label_img.ndim表示共享角落的像素将被视为邻居。- mode字符串,取值范围为 {‘thick’, ‘inner’, ‘outer’, ‘subpixel’}
如何标记边界
thick:任何未完全被相同标签的像素(由
connectivity定义)包围的像素都被标记为边界。这将导致边界为 2 个像素厚。inner:描绘物体内部的像素,保持背景像素不变。
outer:描绘物体边界周围背景中的像素。当两个物体接触时,它们的边界也会被标记。
subpixel:返回一个加倍的图像,其中原始像素之间的像素在适当的情况下被标记为边界。
- background整数,可选
对于模式“inner”和“outer”,需要定义背景标签。有关这两个的描述,请参阅
mode。
- 返回:
- boundaries布尔数组,与
label_img的形状相同 一个布尔图像,其中
True表示边界像素。对于mode等于“subpixel”的情况,对于所有i,boundaries.shape[i]等于2 * label_img.shape[i] - 1(在所有其他像素对之间插入一个像素)。
- boundaries布尔数组,与
示例
>>> labels = np.array([[0, 0, 0, 0, 0, 0, 0, 0, 0, 0], ... [0, 0, 0, 0, 0, 0, 0, 0, 0, 0], ... [0, 0, 0, 0, 0, 5, 5, 5, 0, 0], ... [0, 0, 1, 1, 1, 5, 5, 5, 0, 0], ... [0, 0, 1, 1, 1, 5, 5, 5, 0, 0], ... [0, 0, 1, 1, 1, 5, 5, 5, 0, 0], ... [0, 0, 0, 0, 0, 5, 5, 5, 0, 0], ... [0, 0, 0, 0, 0, 0, 0, 0, 0, 0], ... [0, 0, 0, 0, 0, 0, 0, 0, 0, 0]], dtype=np.uint8) >>> find_boundaries(labels, mode='thick').astype(np.uint8) array([[0, 0, 0, 0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 1, 1, 1, 0, 0], [0, 0, 1, 1, 1, 1, 1, 1, 1, 0], [0, 1, 1, 1, 1, 1, 0, 1, 1, 0], [0, 1, 1, 0, 1, 1, 0, 1, 1, 0], [0, 1, 1, 1, 1, 1, 0, 1, 1, 0], [0, 0, 1, 1, 1, 1, 1, 1, 1, 0], [0, 0, 0, 0, 0, 1, 1, 1, 0, 0], [0, 0, 0, 0, 0, 0, 0, 0, 0, 0]], dtype=uint8) >>> find_boundaries(labels, mode='inner').astype(np.uint8) array([[0, 0, 0, 0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 1, 1, 1, 0, 0], [0, 0, 1, 1, 1, 1, 0, 1, 0, 0], [0, 0, 1, 0, 1, 1, 0, 1, 0, 0], [0, 0, 1, 1, 1, 1, 0, 1, 0, 0], [0, 0, 0, 0, 0, 1, 1, 1, 0, 0], [0, 0, 0, 0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0, 0, 0, 0]], dtype=uint8) >>> find_boundaries(labels, mode='outer').astype(np.uint8) array([[0, 0, 0, 0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 1, 1, 1, 0, 0], [0, 0, 1, 1, 1, 1, 0, 0, 1, 0], [0, 1, 0, 0, 1, 1, 0, 0, 1, 0], [0, 1, 0, 0, 1, 1, 0, 0, 1, 0], [0, 1, 0, 0, 1, 1, 0, 0, 1, 0], [0, 0, 1, 1, 1, 1, 0, 0, 1, 0], [0, 0, 0, 0, 0, 1, 1, 1, 0, 0], [0, 0, 0, 0, 0, 0, 0, 0, 0, 0]], dtype=uint8) >>> labels_small = labels[::2, ::3] >>> labels_small array([[0, 0, 0, 0], [0, 0, 5, 0], [0, 1, 5, 0], [0, 0, 5, 0], [0, 0, 0, 0]], dtype=uint8) >>> find_boundaries(labels_small, mode='subpixel').astype(np.uint8) array([[0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 1, 1, 1, 0], [0, 0, 0, 1, 0, 1, 0], [0, 1, 1, 1, 0, 1, 0], [0, 1, 0, 1, 0, 1, 0], [0, 1, 1, 1, 0, 1, 0], [0, 0, 0, 1, 0, 1, 0], [0, 0, 0, 1, 1, 1, 0], [0, 0, 0, 0, 0, 0, 0]], dtype=uint8) >>> bool_image = np.array([[False, False, False, False, False], ... [False, False, False, False, False], ... [False, False, True, True, True], ... [False, False, True, True, True], ... [False, False, True, True, True]], ... dtype=bool) >>> find_boundaries(bool_image) array([[False, False, False, False, False], [False, False, True, True, True], [False, True, True, True, True], [False, True, True, False, False], [False, True, True, False, False]])
- skimage.segmentation.flood(image, seed_point, *, footprint=None, connectivity=None, tolerance=None)[source]#
与洪水填充相对应的掩码。
从特定的
seed_point开始,找到与种子值相等或在tolerance范围内的连接点。- 参数:
- imagendarray
一个 n 维数组。
- seed_point元组或整数
在
image中用作洪水填充起点的点。如果图像为 1D,则此点可以给定为整数。- footprintndarray,可选
用于确定每个评估像素的邻域的足迹(结构元素)。它必须仅包含 1 和 0,并且具有与
image相同的维度数。如果未给出,则所有相邻像素都视为邻域的一部分(完全连接)。- connectivity整数,可选
用于确定每个评估像素的邻域的数字。与中心距离的平方小于或等于
connectivity的相邻像素被视为邻居。如果footprint不为 None,则忽略此参数。- tolerance浮点数或整数,可选
如果为 None(默认值),则相邻值必须严格等于
image在seed_point的初始值。这是最快的。如果给出一个值,则将在每个点进行比较,如果在初始值的公差范围内,也会被填充(包含在内)。
- 返回:
- maskndarray
返回一个与
image形状相同的布尔数组,其中与种子点连接且相等(或在公差范围内)的区域的值为 True。所有其他值为 False。
注释
此操作的概念类比是许多栅格图形程序中的“油漆桶”工具。此函数仅返回表示填充的掩码。
如果出于内存原因需要索引而不是掩码,则用户可以简单地在结果上运行
numpy.nonzero,保存索引,并丢弃此掩码。示例
>>> from skimage.morphology import flood >>> image = np.zeros((4, 7), dtype=int) >>> image[1:3, 1:3] = 1 >>> image[3, 0] = 1 >>> image[1:3, 4:6] = 2 >>> image[3, 6] = 3 >>> image array([[0, 0, 0, 0, 0, 0, 0], [0, 1, 1, 0, 2, 2, 0], [0, 1, 1, 0, 2, 2, 0], [1, 0, 0, 0, 0, 0, 3]])
用 5 填充连接的 1,具有完全连接性(包括对角线)
>>> mask = flood(image, (1, 1)) >>> image_flooded = image.copy() >>> image_flooded[mask] = 5 >>> image_flooded array([[0, 0, 0, 0, 0, 0, 0], [0, 5, 5, 0, 2, 2, 0], [0, 5, 5, 0, 2, 2, 0], [5, 0, 0, 0, 0, 0, 3]])
用 5 填充连接的 1,排除对角点(连通性 1)
>>> mask = flood(image, (1, 1), connectivity=1) >>> image_flooded = image.copy() >>> image_flooded[mask] = 5 >>> image_flooded array([[0, 0, 0, 0, 0, 0, 0], [0, 5, 5, 0, 2, 2, 0], [0, 5, 5, 0, 2, 2, 0], [1, 0, 0, 0, 0, 0, 3]])
用容差填充
>>> mask = flood(image, (0, 0), tolerance=1) >>> image_flooded = image.copy() >>> image_flooded[mask] = 5 >>> image_flooded array([[5, 5, 5, 5, 5, 5, 5], [5, 5, 5, 5, 2, 2, 5], [5, 5, 5, 5, 2, 2, 5], [5, 5, 5, 5, 5, 5, 3]])
- skimage.segmentation.flood_fill(image, seed_point, new_value, *, footprint=None, connectivity=None, tolerance=None, in_place=False)[source]#
在图像上执行洪水填充。
从特定的
seed_point开始,查找与种子值相等或在tolerance范围内的相连点,然后将这些点设置为new_value。- 参数:
- imagendarray
一个 n 维数组。
- seed_point元组或整数
在
image中用作洪水填充起点的点。如果图像为 1D,则此点可以给定为整数。- new_value
image类型 用于设置整个填充区域的新值。此值必须与
image的 dtype 一致。- footprintndarray,可选
用于确定每个评估像素的邻域的足迹(结构元素)。它必须仅包含 1 和 0,并且具有与
image相同的维度数。如果未给出,则所有相邻像素都视为邻域的一部分(完全连接)。- connectivity整数,可选
用于确定每个评估像素的邻域的数字。与中心距离的平方小于或等于
connectivity的相邻像素被视为邻居。如果footprint不为 None,则忽略此参数。- tolerance浮点数或整数,可选
如果为 None (默认值),则相邻的值必须严格等于
image在seed_point处的值才能被填充。这是最快的。如果提供了容差,则会填充与种子点的值相差正负容差范围内的相邻点(包括边界值)。- in_placebool,可选
如果为 True,则在原地对
image应用洪水填充。如果为 False,则返回洪水填充的结果,而不修改输入image(默认值)。
- 返回:
- filledndarray
返回一个与
image形状相同的数组,其中与种子点相连且相等(或在容差范围内)的区域中的值会被替换为new_value。
注释
此操作的概念类比是许多光栅图形程序中的“油漆桶”工具。
示例
>>> from skimage.morphology import flood_fill >>> image = np.zeros((4, 7), dtype=int) >>> image[1:3, 1:3] = 1 >>> image[3, 0] = 1 >>> image[1:3, 4:6] = 2 >>> image[3, 6] = 3 >>> image array([[0, 0, 0, 0, 0, 0, 0], [0, 1, 1, 0, 2, 2, 0], [0, 1, 1, 0, 2, 2, 0], [1, 0, 0, 0, 0, 0, 3]])
用 5 填充连接的 1,具有完全连接性(包括对角线)
>>> flood_fill(image, (1, 1), 5) array([[0, 0, 0, 0, 0, 0, 0], [0, 5, 5, 0, 2, 2, 0], [0, 5, 5, 0, 2, 2, 0], [5, 0, 0, 0, 0, 0, 3]])
用 5 填充连接的 1,排除对角点(连通性 1)
>>> flood_fill(image, (1, 1), 5, connectivity=1) array([[0, 0, 0, 0, 0, 0, 0], [0, 5, 5, 0, 2, 2, 0], [0, 5, 5, 0, 2, 2, 0], [1, 0, 0, 0, 0, 0, 3]])
用容差填充
>>> flood_fill(image, (0, 0), 5, tolerance=1) array([[5, 5, 5, 5, 5, 5, 5], [5, 5, 5, 5, 2, 2, 5], [5, 5, 5, 5, 2, 2, 5], [5, 5, 5, 5, 5, 5, 3]])
- skimage.segmentation.inverse_gaussian_gradient(image, alpha=100.0, sigma=5.0)[source]#
梯度大小的倒数。
计算图像中梯度的幅度,然后在 [0, 1] 范围内反转结果。平坦区域被赋予接近 1 的值,而接近边界的区域被赋予接近 0 的值。
在调用
morphological_geodesic_active_contour之前,应该将此函数或用户定义的类似函数应用到图像上作为预处理步骤。- 参数:
- image(M, N) 或 (L, M, N) 数组
灰度图像或体数据。
- alphafloat,可选
控制反转的陡峭程度。较大的值将使结果数组中平坦区域和边界区域之间的过渡更加陡峭。
- sigma浮点数,可选
应用于图像的高斯滤波器的标准差。
- 返回:
- gimage(M, N) 或 (L, M, N) 数组
适合于
morphological_geodesic_active_contour的预处理图像(或体数据)。
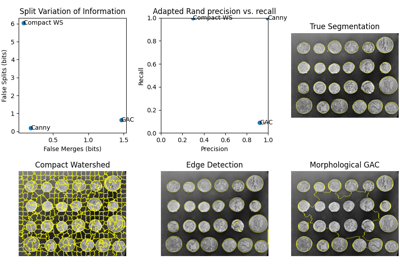
- skimage.segmentation.join_segmentations(s1, s2, return_mapping: bool = False)[source]#
返回两个输入分割的连接。
S1 和 S2 的连接 J 定义为这样一个分割:当且仅当两个体素在 S1 和 S2 中都位于同一分割区域时,它们才位于同一分割区域。
- 参数:
- s1, s2numpy 数组
s1 和 s2 是形状相同的标签字段。
- return_mappingbool,可选
如果为 true,则返回连接分割标签到原始标签的映射。
- 返回:
- jnumpy 数组
s1 和 s2 的连接分割。
- map_j_to_s1ArrayMap,可选
从连接分割 j 的标签到 s1 的标签的映射。
- map_j_to_s2ArrayMap,可选
从连接分割 j 的标签到 s2 的标签的映射。
示例
>>> from skimage.segmentation import join_segmentations >>> s1 = np.array([[0, 0, 1, 1], ... [0, 2, 1, 1], ... [2, 2, 2, 1]]) >>> s2 = np.array([[0, 1, 1, 0], ... [0, 1, 1, 0], ... [0, 1, 1, 1]]) >>> join_segmentations(s1, s2) array([[0, 1, 3, 2], [0, 5, 3, 2], [4, 5, 5, 3]]) >>> j, m1, m2 = join_segmentations(s1, s2, return_mapping=True) >>> m1 ArrayMap(array([0, 1, 2, 3, 4, 5]), array([0, 0, 1, 1, 2, 2])) >>> np.all(m1[j] == s1) True >>> np.all(m2[j] == s2) True
- skimage.segmentation.mark_boundaries(image, label_img, color=(1, 1, 0), outline_color=None, mode='outer', background_label=0)[source]#
返回突出显示标记区域之间边界的图像。
- 参数:
- image(M, N[, 3]) 数组
灰度或 RGB 图像。
- label_img(M, N) int 型数组
标签数组,其中区域由不同的整数值标记。
- color长度为 3 的序列,可选
输出图像中边界的 RGB 颜色。
- outline_color长度为 3 的序列,可选
输出图像中边界周围的 RGB 颜色。如果为 None,则不绘制轮廓。
- mode字符串,取值 {‘thick’, ‘inner’, ‘outer’, ‘subpixel’},可选
查找边界的模式。
- background_labelint,可选
要将哪个标签视为背景(这仅对
inner和outer模式有用)。
- 返回:
- marked(M, N, 3) 浮点数数组
一个图像,其中标签之间的边界叠加在原始图像上。
另请参阅
- skimage.segmentation.morphological_chan_vese(image, num_iter, init_level_set='checkerboard', smoothing=1, lambda1=1, lambda2=1, iter_callback=<function <lambda>>)[source]#
无边缘的形态学主动轮廓(MorphACWE)
使用形态学算子实现的无边缘活动轮廓。它可以用于分割图像和体数据中没有明确边界的对象。要求对象的内部平均看起来与外部不同(即,对象的内部区域平均应该比外部区域更暗或更亮)。
- 参数:
- image(M, N) 或 (L, M, N) 数组
要分割的灰度图像或体数据。
- num_iteruint
要运行的迭代次数
- init_level_set字符串,(M, N) 数组或 (L, M, N) 数组
初始水平集。如果给定了数组,则将其二值化并用作初始水平集。如果给定了字符串,则它定义了使用
image的形状生成合理初始水平集的方法。接受的值为“checkerboard”和“disk”。有关如何创建这些水平集的详细信息,请参阅checkerboard_level_set和disk_level_set的文档。- smoothinguint,可选
每次迭代应用平滑算子的次数。合理的值约为 1-4。较大的值会导致更平滑的分割。
- lambda1float,可选
外部区域的权重参数。如果
lambda1大于lambda2,则外部区域将包含比内部区域更大的值范围。- lambda2float,可选
内部区域的权重参数。如果
lambda2大于lambda1,则内部区域将包含比外部区域更大的值范围。- iter_callback函数,可选
如果给定,则此函数在每次迭代时使用当前水平集作为唯一参数调用一次。这对于调试或在演化过程中绘制中间结果非常有用。
- 返回:
- out(M, N) 或 (L, M, N) 数组
最终分割(即最终水平集)
注释
这是 Chan-Vese 算法的一个版本,它使用形态学算子而不是求解偏微分方程 (PDE) 来演化轮廓。此算法中使用的一组形态学算子被证明与 Chan-Vese PDE 无穷小等价(参见 [1])。但是,形态学算子不会受到 PDE 中常见的数值稳定性问题的困扰(不必为演化寻找正确的时间步长),并且计算速度更快。
该算法及其理论推导在 [1] 中进行了描述。
参考
[1] (1,2)曲线和曲面基于曲率演化的形态学方法,Pablo Márquez-Neila、Luis Baumela、Luis Álvarez。IEEE 模式分析与机器智能汇刊 (PAMI),2014,DOI:10.1109/TPAMI.2013.106
- skimage.segmentation.morphological_geodesic_active_contour(gimage, num_iter, init_level_set='disk', smoothing=1, threshold='auto', balloon=0, iter_callback=<function <lambda>>)[source]#
形态学测地线主动轮廓(MorphGAC)。
使用形态学算子实现的地测活动轮廓。它可用于分割具有可见但噪声、杂乱、断裂边界的对象。
- 参数:
- gimage(M, N) 或 (L, M, N) 数组
要分割的预处理图像或体积。这很少是原始图像。相反,这通常是原始图像的预处理版本,它增强并突出显示要分割对象的边界(或其他结构)。
morphological_geodesic_active_contour()将尝试在gimage较小的区域中停止轮廓演化。请参阅inverse_gaussian_gradient()作为执行此预处理的示例函数。请注意,morphological_geodesic_active_contour()的质量可能很大程度上取决于此预处理。- num_iteruint
要运行的 num_iter 数量。
- init_level_set字符串,(M, N) 数组或 (L, M, N) 数组
初始水平集。如果给定了数组,则将其二值化并用作初始水平集。如果给定了字符串,则它定义了使用
image的形状生成合理初始水平集的方法。接受的值为“checkerboard”和“disk”。有关如何创建这些水平集的详细信息,请参阅checkerboard_level_set和disk_level_set的文档。- smoothinguint,可选
每次迭代应用平滑算子的次数。合理的值约为 1-4。较大的值会导致更平滑的分割。
- thresholdfloat,可选
图像中值小于此阈值的区域将被视为边界。轮廓的演化将停止在这些区域。
- balloonfloat,可选
在图像的非信息区域(即,图像的梯度太小而无法将轮廓推向边界的区域)中引导轮廓的气球力。负值将缩小轮廓,而正值将在这些区域中扩展轮廓。将其设置为零将禁用气球力。
- iter_callback函数,可选
如果给定,则此函数在每次迭代时使用当前水平集作为唯一参数调用一次。这对于调试或在演化过程中绘制中间结果非常有用。
- 返回:
- out(M, N) 或 (L, M, N) 数组
最终分割(即最终水平集)
注释
这是测地活动轮廓 (GAC) 算法的一个版本,它使用形态学算子而不是求解偏微分方程 (PDE) 来演化轮廓。此算法中使用的一组形态学算子被证明与 GAC PDE 无穷小等价(参见 [1])。但是,形态学算子不会受到 PDE 中常见的数值稳定性问题的困扰(例如,不必为演化寻找正确的时间步长),并且计算速度更快。
该算法及其理论推导在 [1] 中进行了描述。
参考
[1] (1,2)曲线和曲面基于曲率演化的形态学方法,Pablo Márquez-Neila、Luis Baumela、Luis Álvarez。IEEE 模式分析与机器智能汇刊 (PAMI),2014,DOI:10.1109/TPAMI.2013.106
- skimage.segmentation.quickshift(image, ratio=1.0, kernel_size=5, max_dist=10, return_tree=False, sigma=0, convert2lab=True, rng=42, *, channel_axis=-1)[source]#
在颜色-(x,y)空间中使用快速移位聚类分割图像。
使用快速移动模式搜索算法生成图像的过度分割。
- 参数:
- image(M, N, C) ndarray
输入图像。可以通过
channel_axis参数指定与颜色通道对应的轴。- ratiofloat,可选,介于 0 和 1 之间
平衡颜色空间邻近度和图像空间邻近度。较高的值会赋予颜色空间更大的权重。
- kernel_sizefloat,可选
用于平滑样本密度的高斯核的宽度。越高意味着聚类越少。
- max_distfloat,可选
数据距离的截止点。越高意味着聚类越少。
- return_treebool,可选
是否返回完整的分割层次结构树和距离。
- sigma浮点数,可选
用于高斯平滑作为预处理的宽度。零表示不平滑。
- convert2labbool,可选
是否应在分割之前将输入转换为 Lab 颜色空间。为此,假设输入为 RGB。
- rng{
numpy.random.Generator, int},可选 伪随机数生成器。默认情况下,使用 PCG64 生成器(参见
numpy.random.default_rng())。如果rng是整数,则用于为生成器设定种子。PRNG 用于打破平局,默认情况下使用 42 作为种子。
- channel_axisint,可选
image中与颜色通道对应的轴。默认为最后一个轴。
- 返回:
- segment_mask(M, N) ndarray
整数掩码,指示分割标签。
注释
作者主张在分割之前将图像转换为 Lab 颜色空间,尽管这不是绝对必要的。为此,必须以 RGB 格式给出图像。
参考
[1]用于模式搜索的快速移动和内核方法,Vedaldi, A. 和 Soatto, S. 欧洲计算机视觉会议,2008
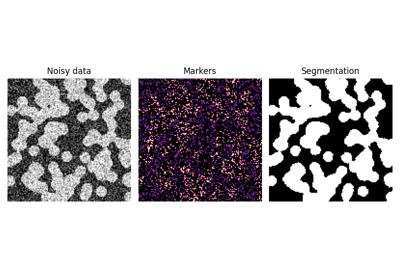
- skimage.segmentation.random_walker(data, labels, beta=130, mode='cg_j', tol=0.001, copy=True, return_full_prob=False, spacing=None, *, prob_tol=0.001, channel_axis=None)[source]#
用于从标记进行分割的随机游走算法。
随机游走算法是为灰度或多通道图像实现的。
- 参数:
- data(M, N[, P][, C]) ndarray
要分割为相的图像。灰度
data可以是二维或三维;多通道数据可以是三维或四维,其中channel_axis指定包含通道的维度。除非使用spacing关键字参数,否则假设数据间距是各向同性的。- labels(M, N[, P]) 整数数组
用于不同阶段的种子标记数组,使用不同的正整数标记。零标记像素是未标记的像素。负标记对应于不考虑的非活动像素(它们会从图中移除)。如果标签不是连续的整数,标签数组将被转换,使得标签是连续的。在多通道情况下,
labels应具有与data的单通道相同的形状,即不包括表示通道的最后一个维度。- betafloat,可选
随机游走运动的惩罚系数(
beta越大,扩散越困难)。- mode字符串,可用选项 {'cg', 'cg_j', 'cg_mg', 'bf'}
在随机游走算法中求解线性系统的模式。
‘bf’(蛮力):计算拉普拉斯矩阵的 LU 分解。对于小型图像(<1024x1024)来说,这很快,但对于大型图像(例如,3D 体积)来说,速度非常慢且占用大量内存。
‘cg’(共轭梯度):使用 scipy.sparse.linalg 中的共轭梯度法迭代求解线性系统。对于大型图像,这种方法比蛮力法占用更少的内存,但速度相当慢。
‘cg_j’(使用雅可比预处理的共轭梯度):在共轭梯度法的迭代过程中应用雅可比预处理器。这可能会加速 ‘cg’ 方法的收敛。
‘cg_mg’(使用多重网格预处理的共轭梯度):使用多重网格求解器计算预处理器,然后使用共轭梯度法计算解。此模式需要安装 pyamg 模块。
- tol浮点数,可选
使用基于共轭梯度的方法('cg','cg_j' 和 'cg_mg')求解线性系统时要达到的容差。
- copy布尔值,可选
如果 copy 为 False,则
labels数组将被分割结果覆盖。如果想节省内存,请使用 copy=False。- return_full_prob布尔值,可选
如果为 True,将返回像素属于每个标签的概率,而不是仅返回最可能的标签。
- spacing浮点数的可迭代对象,可选
每个空间维度中体素之间的间距。如果为
None,则假定每个维度中像素/体素之间的间距为 1。- prob_tol浮点数,可选
结果概率在区间 [0, 1] 内的容差。如果未满足容差,则会显示警告。
- channel_axisint 或 None,可选
如果为 None,则假定图像为灰度(单通道)图像。否则,此参数指示数组的哪个轴对应于通道。
0.19 版本新增:
channel_axis在 0.19 版本中添加。
- 返回:
- outputndarray
如果
return_full_prob为 False,则返回与labels具有相同形状和数据类型的整数数组,其中每个像素已根据各向异性扩散首先到达该像素的标记进行标记。如果
return_full_prob为 True,则返回形状为(nlabels, labels.shape)的浮点数数组。output[label_nb, i, j]是标签label_nb首先到达像素(i, j)的概率。
另请参阅
skimage.segmentation.watershed一种基于数学形态学和从标记“淹没”区域的分割算法。
注释
多通道输入会缩放所有通道数据组合。请确保在运行此算法之前单独归一化所有通道。
spacing参数专门用于各向异性数据集,其中数据点在一个或多个空间维度上的间距不同。各向异性数据在医学成像中很常见。该算法首先在 [1] 中提出。
该算法依次求解每个阶段的标记上放置源的无限时间扩散方程。像素被标记为具有最大概率首先扩散到该像素的阶段。
通过最小化每个阶段的 x.T L x 来求解扩散方程,其中 L 是图像加权图的拉普拉斯矩阵,x 是给定阶段的标记首先通过扩散到达像素的概率(该阶段的标记上 x=1,其他标记上 x=0,并查找其他系数)。每个像素被赋予 x 值最大的标签。图像的拉普拉斯矩阵 L 定义为
L_ii = d_i,像素 i 的邻居数(i 的度)
如果 i 和 j 是相邻像素,则 L_ij = -w_ij
权重 w_ij 是局部梯度范数的递减函数。这确保了相似值的像素之间的扩散更容易。
当拉普拉斯矩阵分解为标记和未标记像素的块时
L = M B.T B A
第一个索引对应于标记的像素,然后对应于未标记的像素,最小化一个阶段的 x.T L x 相当于求解
A x = - B x_m
其中 x_m 在给定阶段的标记上为 1,在其他标记上为 0。此线性系统在算法中使用直接方法求解小型图像,使用迭代方法求解大型图像。
参考
[1]Leo Grady, Random walks for image segmentation, IEEE Trans Pattern Anal Mach Intell. 2006 Nov;28(11):1768-83. DOI:10.1109/TPAMI.2006.233.
示例
>>> rng = np.random.default_rng() >>> a = np.zeros((10, 10)) + 0.2 * rng.random((10, 10)) >>> a[5:8, 5:8] += 1 >>> b = np.zeros_like(a, dtype=np.int32) >>> b[3, 3] = 1 # Marker for first phase >>> b[6, 6] = 2 # Marker for second phase >>> random_walker(a, b) array([[1, 1, 1, 1, 1, 1, 1, 1, 1, 1], [1, 1, 1, 1, 1, 1, 1, 1, 1, 1], [1, 1, 1, 1, 1, 1, 1, 1, 1, 1], [1, 1, 1, 1, 1, 1, 1, 1, 1, 1], [1, 1, 1, 1, 1, 1, 1, 1, 1, 1], [1, 1, 1, 1, 1, 2, 2, 2, 1, 1], [1, 1, 1, 1, 1, 2, 2, 2, 1, 1], [1, 1, 1, 1, 1, 2, 2, 2, 1, 1], [1, 1, 1, 1, 1, 1, 1, 1, 1, 1], [1, 1, 1, 1, 1, 1, 1, 1, 1, 1]], dtype=int32)
- skimage.segmentation.relabel_sequential(label_field, offset=1)[source]#
将任意标签重新标记为 {
offset, …offset+ number_of_labels}。此函数还返回前向映射(将原始标签映射到缩减标签)和反向映射(将缩减标签映射回原始标签)。
- 参数:
- label_fieldint 类型的 numpy 数组,任意形状
标签数组,必须是非负整数。
- offset整数,可选
返回的标签将从
offset开始,该值应严格为正。
- 返回:
- relabeledint 类型的 numpy 数组,与
label_field形状相同 输入的标签字段,其标签映射到 {offset, …, number_of_labels + offset - 1}。数据类型将与
label_field相同,除非 offset + number_of_labels 导致当前数据类型溢出。- forward_mapArrayMap
从原始标签空间到返回标签空间的映射。可用于重新应用相同的映射。有关用法,请参见示例。输出数据类型将与
relabeled相同。- inverse_mapArrayMap
从新标签空间到原始空间的映射。这可用于从重新标记的标签字段重建原始标签字段。输出数据类型将与
label_field相同。
- relabeledint 类型的 numpy 数组,与
注释
标签 0 被假定为表示背景,并且永远不会被重新映射。
对于某些输入,前向映射可能非常大,因为它的长度由标签字段的最大值给出。但是,在大多数情况下,
label_field.max()远小于label_field.size,在这些情况下,保证前向映射小于输入或输出图像。示例
>>> from skimage.segmentation import relabel_sequential >>> label_field = np.array([1, 1, 5, 5, 8, 99, 42]) >>> relab, fw, inv = relabel_sequential(label_field) >>> relab array([1, 1, 2, 2, 3, 5, 4]) >>> print(fw) ArrayMap: 1 → 1 5 → 2 8 → 3 42 → 4 99 → 5 >>> np.array(fw) array([0, 1, 0, 0, 0, 2, 0, 0, 3, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 4, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 5]) >>> np.array(inv) array([ 0, 1, 5, 8, 42, 99]) >>> (fw[label_field] == relab).all() True >>> (inv[relab] == label_field).all() True >>> relab, fw, inv = relabel_sequential(label_field, offset=5) >>> relab array([5, 5, 6, 6, 7, 9, 8])
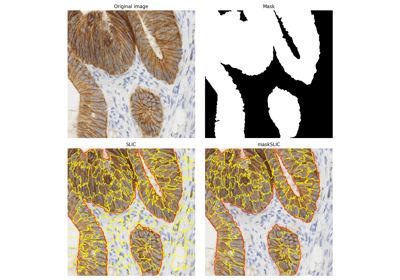
- skimage.segmentation.slic(image, n_segments=100, compactness=10.0, max_num_iter=10, sigma=0, spacing=None, convert2lab=None, enforce_connectivity=True, min_size_factor=0.5, max_size_factor=3, slic_zero=False, start_label=1, mask=None, *, channel_axis=-1)[source]#
在颜色-(x,y,z)空间中使用 k-means 聚类分割图像。
- 参数:
- image(M, N[, P][, C]) ndarray
输入图像。可以是 2D 或 3D,以及灰度或多通道(请参见
channel_axis参数)。输入图像必须是无 NaN 的,或者必须屏蔽 NaN。- n_segments整数,可选
分割输出图像中(近似)标签的数量。
- compactness浮点数,可选
平衡颜色邻近度和空间邻近度。更高的值会给予空间邻近度更高的权重,使得超像素形状更趋向于方形/立方体。在 SLICO 模式下,这是初始紧凑度。此参数强烈依赖于图像对比度和图像中对象的形状。我们建议以对数刻度探索可能的值,例如 0.01、0.1、1、10、100,然后在选定的值附近进行微调。
- max_num_iterint,可选
k 均值算法的最大迭代次数。
- sigma浮点数或浮点数数组,可选
用于图像每个维度预处理的高斯平滑核的宽度。如果为标量值,则相同的 sigma 将应用于每个维度。零表示不平滑。请注意,如果
sigma是标量并且提供了手动体素间距,则会自动缩放(请参阅“注释”部分)。如果 sigma 为数组,则其大小必须与image的空间维度数匹配。- spacing浮点数数组,可选
沿每个空间维度的体素间距。默认情况下,
slic假定均匀间距(沿每个空间维度具有相同的体素分辨率)。此参数控制 k 均值聚类期间沿空间维度的距离的权重。- convert2labbool,可选
是否应在分割之前将输入转换为 Lab 颜色空间。输入图像必须为 RGB。强烈建议这样做。当
channel_axis` is not None *and* ``image.shape[-1] == 3时,此选项默认设置为True。- enforce_connectivity布尔值,可选
生成的分割区域是否连通
- min_size_factor浮点数,可选
要移除的最小分割大小相对于假定分割大小
`depth*width*height/n_segments`的比例- max_size_factor浮点数,可选
最大连通分割区域大小的比例。在大多数情况下,值 3 都可以正常工作。
- slic_zero布尔值,可选
运行 SLIC-zero,SLIC 的零参数模式。[2]
- start_label整数,可选
标签的起始索引。应为 0 或 1。
在 0.17 版本中添加:
start_label在 0.17 版本中引入- maskndarray,可选
如果提供,则仅在 mask 为 True 的位置计算超像素,并且使用 k 均值聚类策略在 mask 上均匀分布种子点。mask 的维度数必须等于图像的空间维度数。
在 0.17 版本中添加:
mask在 0.17 版本中引入- channel_axisint 或 None,可选
如果为 None,则假定图像为灰度(单通道)图像。否则,此参数指示数组的哪个轴对应于通道。
0.19 版本新增:
channel_axis在 0.19 版本中添加。
- 返回:
- labels2D 或 3D 数组
整数掩码,指示分割标签。
- 引发:
- ValueError
如果
convert2lab设置为True,但最后一个数组维度的长度不是 3。- ValueError
如果
start_label不是 0 或 1。- ValueError
如果
image包含未屏蔽的 NaN 值。- ValueError
如果
image包含未屏蔽的无限值。- ValueError
如果
image是 2D 的,但channel_axis是 -1(默认值)。
注释
如果
sigma > 0,则在分割之前使用高斯核平滑图像。如果
sigma是标量,并且提供了spacing,则核宽度沿每个维度除以间距。例如,如果sigma=1且spacing=[5, 1, 1],则有效的sigma为[0.2, 1, 1]。这确保了各向异性图像的合理平滑。图像在处理之前会被重新缩放到 [0, 1] 范围内(忽略屏蔽值)。
默认情况下,形状为 (M, N, 3) 的图像被解释为 2D RGB 图像。要将它们解释为最后一个维度长度为 3 的 3D 图像,请使用
channel_axis=None。引入
start_label是为了解决问题 [4]。默认情况下,标签索引从 1 开始。
参考
[1]Radhakrishna Achanta、Appu Shaji、Kevin Smith、Aurelien Lucchi、Pascal Fua 和 Sabine Süsstrunk,“SLIC Superpixels Compared to State-of-the-art Superpixel Methods”,TPAMI,2012 年 5 月。DOI:10.1109/TPAMI.2012.120
[3]Irving, Benjamin. “maskSLIC:区域超像素生成及其在医学图像中局部病理表征中的应用”,2016 年,arXiv:1606.09518
示例
>>> from skimage.segmentation import slic >>> from skimage.data import astronaut >>> img = astronaut() >>> segments = slic(img, n_segments=100, compactness=10)
增加紧凑度参数会产生更多方形区域
>>> segments = slic(img, n_segments=100, compactness=20)
- skimage.segmentation.watershed(image, markers=None, connectivity=1, offset=None, mask=None, compactness=0, watershed_line=False)[source]#
在从给定标记填充的图像中查找分水岭盆地。
- 参数:
- image(M, N[, …]) ndarray
数据数组,其中首先标记最低值点。
- markers整数,或 (M, N[, …]) 整数数组,可选
所需的盆地数量,或标记盆地的数组,其中包含要在标签矩阵中分配的值。零表示不是标记。如果为 None(默认),则标记被确定为
image的局部最小值。具体而言,计算等效于对image应用skimage.morphology.local_minima(),然后对结果应用skimage.measure.label()(具有相同的给定connectivity)。一般来说,鼓励用户显式传递标记。- connectivity整数或 ndarray,可选
邻域连通性。整数的解释方式与
scipy.ndimage.generate_binary_structure中相同,表示到达邻居的最大正交步数。数组被直接解释为足迹(结构元素)。默认值为 1。在 2D 中,1 表示 4 邻域,而 2 表示 8 邻域。- offset类似数组,形状为 image.ndim,可选
足迹中心的坐标。
- mask(M, N[, …]) 布尔值或 0 和 1 的 ndarray,可选
与
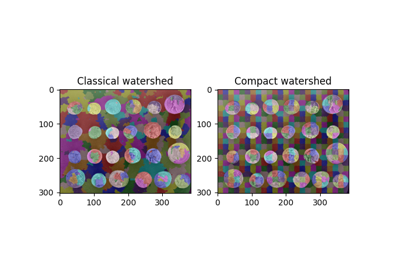
image形状相同的数组。仅标记 mask == True 的点。- compactness浮点数,可选
使用具有给定紧凑度参数的紧凑分水岭 [1]。更高的值会导致形状更规则的分水岭盆地。
- watershed_line布尔值,可选
如果为 True,则宽度为一个像素的线分隔分水岭算法获得的区域。该线的标签为 0。请注意,用于添加此线的方法期望标记区域不相邻;分水岭线可能不会捕获相邻标记区域之间的边界。
- 返回:
- outndarray
与
markers具有相同类型和形状的标记矩阵。
另请参阅
skimage.segmentation.random_walker一种基于各向异性扩散的分割算法,通常比分水岭慢,但在噪声数据和有孔边界上效果良好。
注释
此函数实现一种分水岭算法 [2] [3],该算法将像素分配到标记的盆地中。该算法使用优先级队列来保存像素,其中优先级队列的度量标准是像素值,然后是进入队列的时间 - 这会解决偏向于最近标记的平局。
一些想法来自 [4]。论文中最重要的见解是,进入队列的时间解决了两个问题:像素应分配给具有最大梯度的邻居,或者,如果没有梯度,则平台上的像素应在相对侧的标记之间分割。
此实现将所有参数转换为特定的、最小公分母类型,然后将它们传递给 C 算法。
可以使用手动方式确定标记,也可以使用自动方式,例如使用图像梯度的局部最小值,或者使用到背景的距离函数的局部最大值来分离重叠的对象(请参见示例)。
参考
[1]P. Neubert 和 P. Protzel,“Compact Watershed and Preemptive SLIC: On Improving Trade-offs of Superpixel Segmentation Algorithms”,2014 年第 22 届国际模式识别会议,斯德哥尔摩,瑞典,2014 年,第 996-1001 页,DOI:10.1109/ICPR.2014.181 https://www.tu-chemnitz.de/etit/proaut/publications/cws_pSLIC_ICPR.pdf
[4]P. J. Soille 和 M. M. Ansoult,“Automated basin delineation from digital elevation models using mathematical morphology”,Signal Processing,20(2):171-182,DOI:10.1016/0165-1684(90)90127-K
示例
分水岭算法可用于分离重叠的对象。
我们首先生成一个带有两个重叠圆的初始图像
>>> x, y = np.indices((80, 80)) >>> x1, y1, x2, y2 = 28, 28, 44, 52 >>> r1, r2 = 16, 20 >>> mask_circle1 = (x - x1)**2 + (y - y1)**2 < r1**2 >>> mask_circle2 = (x - x2)**2 + (y - y2)**2 < r2**2 >>> image = np.logical_or(mask_circle1, mask_circle2)
接下来,我们想要分离这两个圆。我们在到背景的距离的最大值处生成标记
>>> from scipy import ndimage as ndi >>> distance = ndi.distance_transform_edt(image) >>> from skimage.feature import peak_local_max >>> max_coords = peak_local_max(distance, labels=image, ... footprint=np.ones((3, 3))) >>> local_maxima = np.zeros_like(image, dtype=bool) >>> local_maxima[tuple(max_coords.T)] = True >>> markers = ndi.label(local_maxima)[0]
最后,我们在图像和标记上运行分水岭算法
>>> labels = watershed(-distance, markers, mask=image)
该算法也适用于 3D 图像,例如可以用来分离重叠的球体。