skimage.transform#
几何变换和其他变换,例如,旋转、Radon 变换。
几何变换:这些变换会改变图像的形状或位置。它们对于诸如图像配准、对齐和几何校正等任务非常有用。示例:
AffineTransform、ProjectiveTransform、EuclideanTransform。图像大小调整和重新缩放:这些变换会更改图像的大小或分辨率。它们对于诸如下采样图像以减小其大小或上采样图像以增加其分辨率等任务非常有用。示例:
resize()、rescale()。特征检测和提取:这些变换识别和提取图像中的特定特征或模式。它们对于诸如对象检测、图像分割和特征匹配等任务非常有用。示例:
hough_circle()、pyramid_expand()、radon()。图像变换:这些变换改变图像的外观而不改变其内容。它们对于诸如创建图像马赛克、应用艺术效果和可视化图像数据等任务非常有用。示例:
warp()、iradon()。
通过局部平均对 N 维图像进行下采样。 |
|
估计 2D 几何变换参数。 |
|
计算输入数组的二维有限 Radon 变换 (FRT)。 |
|
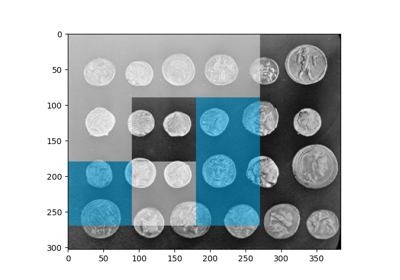
执行圆形霍夫变换。 |
|
返回圆形霍夫变换中的峰值。 |
|
执行椭圆霍夫变换。 |
|
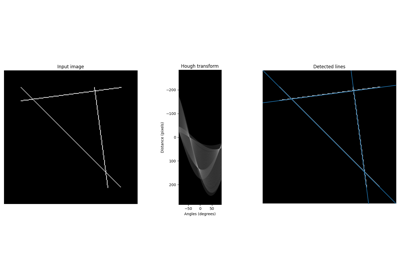
执行直线霍夫变换。 |
|
返回直线霍夫变换中的峰值。 |
|
计算输入数组的二维逆有限 Radon 变换 (iFRT)。 |
|
积分图像/求和区域表。 |
|
使用积分图像在给定窗口上积分。 |
|
逆拉东变换。 |
|
逆拉东变换。 |
|
应用 2D 矩阵变换。 |
|
排序角度以减少后续投影中相关信息的量。 |
|
从渐进式概率线霍夫变换返回线。 |
|
上采样然后平滑图像。 |
|
生成输入图像形成的 Gaussian 金字塔的图像。 |
|
生成输入图像形成的拉普拉斯金字塔的图像。 |
|
平滑然后下采样图像。 |
|
计算给定指定投影角度的图像的拉东变换。 |
|
按特定因子缩放图像。 |
|
调整图像大小以匹配特定大小。 |
|
使用局部均值/双线性缩放调整数组大小。 |
|
围绕中心将图像旋转特定角度。 |
|
执行漩涡变换。 |
|
根据给定的坐标变换扭曲图像。 |
|
为 2-D 图像扭曲的输出构建源坐标。 |
|
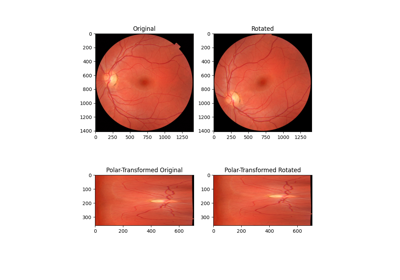
将图像重新映射到极坐标或对数极坐标空间。 |
|
仿射变换。 |
|
基本矩阵变换。 |
|
欧几里得变换,也称为刚性变换。 |
|
基本矩阵变换。 |
|
分段仿射变换。 |
|
2D 多项式变换。 |
|
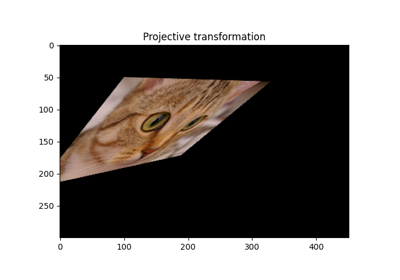
透视变换。 |
|
相似变换。 |
|
薄板样条变换。 |
- skimage.transform.downscale_local_mean(image, factors, cval=0, clip=True)[源代码]#
通过局部平均对 N 维图像进行下采样。
如果图像不能被整数因子完全整除,则用
cval填充图像。与
skimage.transform.resize和skimage.transform.rescale中的插值不同,此函数计算输入图像中大小为factors的每个块中元素的局部平均值。- 参数:
- image(M[, …]) ndarray
输入图像。
- factorsarray_like
包含沿每个轴的下采样整数因子的数组。
- cvalfloat,可选
如果图像不能被整数因子完全整除,则为常数填充值。
- clipbool,可选
未使用,但在此处保留以与此模块中的其他变换保持 API 一致性。(假设提供的
cval也在此范围内,则局部均值将永远不会超出输入图像中值的范围。)
- 返回:
- imagendarray
下采样图像,其维度与输入图像相同。对于整数输入,输出 dtype 将为
float64。有关详细信息,请参阅numpy.mean()。
示例
>>> a = np.arange(15).reshape(3, 5) >>> a array([[ 0, 1, 2, 3, 4], [ 5, 6, 7, 8, 9], [10, 11, 12, 13, 14]]) >>> downscale_local_mean(a, (2, 3)) array([[3.5, 4. ], [5.5, 4.5]])
- skimage.transform.estimate_transform(ttype, src, dst, *args, **kwargs)[源代码]#
估计 2D 几何变换参数。
您可以使用总最小二乘法确定过度、良好和欠定的参数。
源坐标和目标坐标的数量必须匹配。
- 参数:
- ttype{‘euclidean’, similarity’, ‘affine’, ‘piecewise-affine’, ‘projective’, ‘polynomial’}
变换类型。
- kwargsarray_like 或 int
函数参数 (src, dst, n, angle)
NAME / TTYPE FUNCTION PARAMETERS 'euclidean' `src, `dst` 'similarity' `src, `dst` 'affine' `src, `dst` 'piecewise-affine' `src, `dst` 'projective' `src, `dst` 'polynomial' `src, `dst`, `order` (polynomial order, default order is 2)另请参阅下面的示例。
- 返回:
- tform
_GeometricTransform 包含变换参数并提供对正向和逆向变换函数的访问的变换对象。
- tform
示例
>>> import numpy as np >>> import skimage as ski
>>> # estimate transformation parameters >>> src = np.array([0, 0, 10, 10]).reshape((2, 2)) >>> dst = np.array([12, 14, 1, -20]).reshape((2, 2))
>>> tform = ski.transform.estimate_transform('similarity', src, dst)
>>> np.allclose(tform.inverse(tform(src)), src) True
>>> # warp image using the estimated transformation >>> image = ski.data.camera()
>>> ski.transform.warp(image, inverse_map=tform.inverse)
>>> # create transformation with explicit parameters >>> tform2 = ski.transform.SimilarityTransform(scale=1.1, rotation=1, ... translation=(10, 20))
>>> # unite transformations, applied in order from left to right >>> tform3 = tform + tform2 >>> np.allclose(tform3(src), tform2(tform(src))) True
- skimage.transform.frt2(a)[source]#
计算输入数组的二维有限 Radon 变换 (FRT)。
- 参数:
- a整数类型 ndarray,形状为 (M, M)
输入数组。
- 返回:
- FRT整数类型 ndarray,形状为 (M+1, M)
有限拉东变换系数数组。
另请参阅
ifrt2二维逆 FRT。
注释
当且仅当 M 为素数时,FRT 才具有唯一的逆。[FRT] 此算法的思想归功于 Vlad Negnevitski。
参考文献
[FRT]A. Kingston 和 I. Svalbe,“周期离散图像数组上的投影变换”,载于 P. Hawkes (编), 《成像和电子物理学进展》, 139 (2006)
示例
生成测试图像:使用素数作为数组维度
>>> SIZE = 59 >>> img = np.tri(SIZE, dtype=np.int32)
应用有限拉东变换
>>> f = frt2(img)
- skimage.transform.hough_circle(image, radius, normalize=True, full_output=False)[source]#
执行圆形霍夫变换。
- 参数:
- imagendarray,形状为 (M, N)
输入图像,非零值表示边缘。
- radius标量或标量序列
计算霍夫变换的半径。浮点数将转换为整数。
- normalize布尔值,可选
使用绘制半径所需的像素数来标准化累加器。
- full_output布尔值,可选
将输出大小扩展为最大半径的两倍,以便检测输入图片之外的中心。
- 返回:
- Hndarray,形状为 (半径索引, M + 2R, N + 2R)
每个半径的霍夫变换累加器。如果 full_output 为 True,则 R 表示较大半径。否则,R = 0。
示例
>>> from skimage.transform import hough_circle >>> from skimage.draw import circle_perimeter >>> img = np.zeros((100, 100), dtype=bool) >>> rr, cc = circle_perimeter(25, 35, 23) >>> img[rr, cc] = 1 >>> try_radii = np.arange(5, 50) >>> res = hough_circle(img, try_radii) >>> ridx, r, c = np.unravel_index(np.argmax(res), res.shape) >>> r, c, try_radii[ridx] (25, 35, 23)
- skimage.transform.hough_circle_peaks(hspaces, radii, min_xdistance=1, min_ydistance=1, threshold=None, num_peaks=inf, total_num_peaks=inf, normalize=False)[source]#
返回圆形霍夫变换中的峰值。
识别给定霍夫空间中以一定距离分隔的最突出圆形。在霍夫空间的第一和第二维度中分别应用不同大小的非最大抑制来识别峰值。对于半径不同但距离较近的圆,仅保留峰值最高的圆。
- 参数:
- hspaces(M, N, P) 数组
由
hough_circle函数返回的霍夫空间。- radii(M,) 数组
对应于霍夫空间的半径。
- min_xdistanceint,可选
x 维度中分隔中心的最小距离。
- min_ydistanceint,可选
y 维度中分隔中心的最小距离。
- thresholdfloat,可选
每个霍夫空间中峰值的最小强度。默认为
0.5 * max(hspace)。- num_peaksint,可选
每个霍夫空间中的最大峰值数。当峰值数超过
num_peaks时,仅考虑对应半径的基于峰值强度的num_peaks个坐标。- total_num_peaksint,可选
最大峰值数。当峰值数超过
num_peaks时,返回基于峰值强度的num_peaks个坐标。- normalizebool,可选
如果为 True,则通过半径标准化累加器,以对突出峰值进行排序。
- 返回:
- accum, cx, cy, rad数组元组
霍夫空间中的峰值、x 和 y 中心坐标以及半径。
注释
半径较大的圆在霍夫空间中具有较高的峰值。如果优先选择较大的圆而不是较小的圆,则
normalize应为 False。否则,将按照投票数递减的顺序返回圆。示例
>>> from skimage import transform, draw >>> img = np.zeros((120, 100), dtype=int) >>> radius, x_0, y_0 = (20, 99, 50) >>> y, x = draw.circle_perimeter(y_0, x_0, radius) >>> img[x, y] = 1 >>> hspaces = transform.hough_circle(img, radius) >>> accum, cx, cy, rad = hough_circle_peaks(hspaces, [radius,])
- skimage.transform.hough_ellipse(image, threshold=4, accuracy=1, min_size=4, max_size=None)[source]#
执行椭圆霍夫变换。
- 参数:
- image(M, N) ndarray
输入图像,非零值表示边缘。
- thresholdint,可选
累加器阈值。较低的值将返回更多椭圆。
- accuracydouble,可选
累加器中用于短轴的箱体大小。较高的值将返回更多椭圆,但会导致短轴长度的估计不那么精确。
- min_sizeint,可选
最小长轴长度。
- max_sizeint,可选
最大短轴长度。如果为 None,则该值设置为较小图像维度的一半。
- 返回:
- result带有字段 [(accumulator, yc, xc, a, b, orientation)] 的 ndarray。
其中
(yc, xc)是中心,(a, b)分别是长轴和短轴。orientation值遵循skimage.draw.ellipse_perimeter约定。
注释
图像中潜在的椭圆由其长轴和短轴长度表征。对于图像中至少相隔
min_size一半的任何一对非零像素,累加器会跟踪由所有其他非零像素形成的潜在椭圆的短轴长度。如果这些累积的短轴长度的直方图中的任何箱体(具有bin_size = accuracy * accuracy)高于threshold,则将相应的椭圆添加到结果中。因此,较高的
accuracy将导致在图像中找到更多的椭圆,但代价是短轴长度的估计不太精确。参考文献
[1]Xie, Yonghong, and Qiang Ji. “一种新的高效椭圆检测方法。” 《模式识别,2002 年会议论文集》。第 16 届国际会议。卷 2。IEEE,2002
示例
>>> from skimage.transform import hough_ellipse >>> from skimage.draw import ellipse_perimeter >>> img = np.zeros((25, 25), dtype=np.uint8) >>> rr, cc = ellipse_perimeter(10, 10, 6, 8) >>> img[cc, rr] = 1 >>> result = hough_ellipse(img, threshold=8) >>> result.tolist() [(10, 10.0, 10.0, 8.0, 6.0, 0.0)]
- skimage.transform.hough_line(image, theta=None)[source]#
执行直线霍夫变换。
- 参数:
- image(M, N) ndarray
输入图像,非零值表示边缘。
- thetadouble 类型 ndarray,形状为 (K,),可选
计算变换的角度,以弧度为单位。默认为 180 个角度的向量,均匀分布在范围 [-pi/2, pi/2) 中。
- 返回:
- hspaceuint64 类型 ndarray,形状为 (P, Q)
霍夫变换累加器。
- anglesndarray
计算变换的角度,以弧度为单位。
- distancesndarray
距离值。
注释
原点是原始图像的左上角。 X 轴和 Y 轴分别是水平和垂直边缘。距离是从原点到检测到的线的最小代数距离。通过减小
theta数组中的步长,可以提高角度精度。示例
生成测试图像
>>> img = np.zeros((100, 150), dtype=bool) >>> img[30, :] = 1 >>> img[:, 65] = 1 >>> img[35:45, 35:50] = 1 >>> for i in range(90): ... img[i, i] = 1 >>> rng = np.random.default_rng() >>> img += rng.random(img.shape) > 0.95
应用霍夫变换
>>> out, angles, d = hough_line(img)
- skimage.transform.hough_line_peaks(hspace, angles, dists, min_distance=9, min_angle=10, threshold=None, num_peaks=inf)[源代码]#
返回直线霍夫变换中的峰值。
在霍夫变换中识别以一定角度和距离分隔的最突出的直线。在霍夫空间的第一个(距离)和第二个(角度)维度中分别应用不同大小的非极大值抑制来识别峰值。
- 参数:
- hspacendarray,形状为 (M, N)
由
hough_line函数返回的霍夫空间。- anglesarray,形状为 (N,)
由
hough_line函数返回的角度。假设是连续的。(angles[-1] - angles[0] == PI)。- distsarray,形状为 (M,)
由
hough_line函数返回的距离。- min_distanceint,可选
分隔直线的最小距离(霍夫空间第一维的最大滤波器大小)。
- min_angleint,可选
分隔直线的最小角度(霍夫空间第二维的最大滤波器大小)。
- thresholdfloat,可选
峰值的最小强度。默认值为
0.5 * max(hspace)。- num_peaksint,可选
最大峰值数。当峰值数超过
num_peaks时,返回基于峰值强度的num_peaks个坐标。
- 返回:
- accum, angles, dists数组元组
霍夫空间中的峰值、角度和距离。
示例
>>> from skimage.transform import hough_line, hough_line_peaks >>> from skimage.draw import line >>> img = np.zeros((15, 15), dtype=bool) >>> rr, cc = line(0, 0, 14, 14) >>> img[rr, cc] = 1 >>> rr, cc = line(0, 14, 14, 0) >>> img[cc, rr] = 1 >>> hspace, angles, dists = hough_line(img) >>> hspace, angles, dists = hough_line_peaks(hspace, angles, dists) >>> len(angles) 2
- skimage.transform.ifrt2(a)[源代码]#
计算输入数组的二维逆有限 Radon 变换 (iFRT)。
- 参数:
- andarray of int,形状为 (M+1, M)
输入数组。
- 返回:
- iFRTndarray of int,形状为 (M, M)
反有限拉东变换系数。
另请参阅
frt2二维 FRT
注释
当且仅当 M 为素数时,FRT 才具有唯一的逆。有关概述,请参阅 [1]。此算法的想法归功于 Vlad Negnevitski。
参考文献
[1]A. Kingston 和 I. Svalbe,“周期离散图像数组上的投影变换”,载于 P. Hawkes (编), 《成像和电子物理学进展》, 139 (2006)
示例
>>> SIZE = 59 >>> img = np.tri(SIZE, dtype=np.int32)
应用有限拉东变换
>>> f = frt2(img)
应用反有限拉东变换以恢复输入
>>> fi = ifrt2(f)
检查它是否与原始值相同
>>> assert len(np.nonzero(img-fi)[0]) == 0
- skimage.transform.integral_image(image, *, dtype=None)[源代码]#
积分图像/求和区域表。
积分图像包含其上方和左侧所有元素的总和,即
\[S[m, n] = \sum_{i \leq m} \sum_{j \leq n} X[i, j]\]- 参数:
- imagendarray
输入图像。
- 返回:
- Sndarray
与输入图像形状相同的积分图像/求和面积表。
注释
为了获得更高的精度并避免潜在的溢出,当使用默认的 None dtype 时,输出的数据类型可能与输入的类型不同。 对于具有整数 dtype 的输入,其行为与
numpy.cumsum()的行为匹配。浮点输入将被提升为至少双精度。 用户可以设置dtype来覆盖此行为。参考文献
[1]F.C. Crow, “用于纹理映射的求和面积表,”ACM SIGGRAPH 计算机图形,第 18 卷,1984 年,第 207-212 页。
- skimage.transform.integrate(ii, start, end)[源代码]#
使用积分图像在给定窗口上积分。
- 参数:
- iindarray
积分图像。
- start元组列表,每个元组的长度等于
ii的维度 窗口左上角的坐标。列表中的每个元组都包含起始的行、列、…索引,即
[(row_win1, col_win1, ...), (row_win2, col_win2,...), ...]。- end元组列表,每个元组的长度等于
ii的维度 窗口右下角的坐标。列表中的每个元组都包含结束的行、列、…索引,即
[(row_win1, col_win1, ...), (row_win2, col_win2, ...), ...]。
- 返回:
- S标量或 ndarray
给定窗口上的积分(总和)。
另请参阅
integral_image创建积分图像/求和面积表。
示例
>>> arr = np.ones((5, 6), dtype=float) >>> ii = integral_image(arr) >>> integrate(ii, (1, 0), (1, 2)) # sum from (1, 0) to (1, 2) array([3.]) >>> integrate(ii, [(3, 3)], [(4, 5)]) # sum from (3, 3) to (4, 5) array([6.]) >>> # sum from (1, 0) to (1, 2) and from (3, 3) to (4, 5) >>> integrate(ii, [(1, 0), (3, 3)], [(1, 2), (4, 5)]) array([3., 6.])
- skimage.transform.iradon(radon_image, theta=None, output_size=None, filter_name='ramp', interpolation='linear', circle=True, preserve_range=True)[源代码]#
逆拉东变换。
使用滤波反投影算法,从拉东变换重建图像。
- 参数:
- radon_imagendarray
包含拉东变换的图像(正弦图)。图像的每一列对应于沿不同角度的投影。断层扫描旋转轴应位于
radon_image的第 0 维度上的像素索引radon_image.shape[0] // 2处。- thetaarray,可选
重建角度(以度为单位)。默认值:m 个角度均匀分布在 0 到 180 之间(如果
radon_image的形状为 (N, M))。- output_sizeint,可选
重建中的行数和列数。
- filter_namestr,可选
频域滤波中使用的滤波器。默认使用斜坡滤波器。 可用的滤波器:ramp、shepp-logan、cosine、hamming、hann。指定 None 以不使用滤波器。
- interpolationstr,可选
重建中使用的插值方法。 可用的方法:‘linear’、‘nearest’ 和 ‘cubic’(‘cubic’ 较慢)。
- circleboolean,可选
假设重建后的图像在内切圆外为零。还更改默认的 output_size 以匹配调用
circle=True的radon的行为。- preserve_rangebool,可选
是否保留原始值范围。 否则,将根据
img_as_float的约定转换输入图像。另请参阅 https://scikit-image.cn/docs/dev/user_guide/data_types.html
- 返回:
- reconstructedndarray
重建图像。旋转轴将位于索引为
(reconstructed.shape[0] // 2, reconstructed.shape[1] // 2)的像素中。
0.19 版本更改: 在
iradon中,filter参数已被弃用,推荐使用filter_name。
注释
它应用傅里叶切片定理,通过将滤波器的频域与投影数据的 FFT 相乘来重建图像。此算法称为滤波反投影。
参考文献
[1]AC Kak, M Slaney, “Principles of Computerized Tomographic Imaging”, IEEE Press 1988.
[2]B.R. Ramesh, N. Srinivasa, K. Rajgopal, “An Algorithm for Computing the Discrete Radon Transform With Some Applications”, Proceedings of the Fourth IEEE Region 10 International Conference, TENCON ‘89, 1989
- skimage.transform.iradon_sart(radon_image, theta=None, image=None, projection_shifts=None, clip=None, relaxation=0.15, dtype=None)[源代码]#
逆拉东变换。
使用同步代数重建技术 (SART) 算法的单次迭代,从拉东变换重建图像。
- 参数:
- radon_imagendarray,形状 (M, N)
包含拉东变换的图像(正弦图)。图像的每一列对应于沿不同角度的投影。断层扫描旋转轴应位于
radon_image的第 0 维度上的像素索引radon_image.shape[0] // 2处。- thetaarray,形状 (N,),可选
重建角度(以度为单位)。默认值:m 个角度均匀分布在 0 到 180 之间(如果
radon_image的形状为 (N, M))。- imagendarray,形状 (M, M),可选
包含初始重建估计的图像。默认值是零数组。
- projection_shiftsarray,形状 (N,),可选
在重建图像之前,将
radon_image(正弦图)中包含的投影移动这么多像素。第 i 个值定义radon_image的第 i 列的偏移。- clip长度为 2 的浮点数序列,可选
强制重建断层扫描图中的所有值都位于范围
[clip[0], clip[1]]内- relaxationfloat,可选
更新步骤的松弛参数。较高的值可以提高收敛速度,但可能会导致不稳定。不建议使用接近或高于 1 的值。
- dtypedtype,可选
输出数据类型,必须是浮点型。默认情况下,如果输入数据类型不是 float,则输入将转换为 double,否则 dtype 设置为输入数据类型。
- 返回:
- reconstructedndarray
重建图像。旋转轴将位于索引为
(reconstructed.shape[0] // 2, reconstructed.shape[1] // 2)的像素中。
注释
代数重建技术基于将断层扫描重建问题表述为一组线性方程。沿着每条射线,投影值是沿该射线的横截面的所有值的总和。SART(以及代数技术的其他一些变体)的典型特征是,它使用横截面像素值之间的线性插值,在沿射线的等距点处对横截面进行采样。然后使用略微修改的 Kaczmarz 方法求解生成的线性方程组。
使用 SART 时,通常一次迭代就足以获得良好的重建。进一步迭代将倾向于增强高频信息,但通常也会增加噪声。
参考文献
[1]AC Kak, M Slaney, “Principles of Computerized Tomographic Imaging”, IEEE Press 1988.
[2]AH Andersen, AC Kak, “Simultaneous algebraic reconstruction technique (SART): a superior implementation of the ART algorithm”, Ultrasonic Imaging 6 pp 81–94 (1984)
[3]S Kaczmarz, “Angenäherte auflösung von systemen linearer gleichungen”, Bulletin International de l’Academie Polonaise des Sciences et des Lettres 35 pp 355–357 (1937)
[4]Kohler, T. “A projection access scheme for iterative reconstruction based on the golden section.” Nuclear Science Symposium Conference Record, 2004 IEEE. Vol. 6. IEEE, 2004.
[5]Kaczmarz' 方法,维基百科,https://en.wikipedia.org/wiki/Kaczmarz_method
- skimage.transform.matrix_transform(coords, matrix)[源代码]#
应用 2D 矩阵变换。
- 参数:
- coords(N, 2) 类数组
要转换的 x, y 坐标
- matrix(3, 3) 类数组
齐次变换矩阵。
- 返回:
- coords(N, 2) 数组
变换后的坐标。
- skimage.transform.order_angles_golden_ratio(theta)[源代码]#
排序角度以减少后续投影中相关信息的量。
- 参数:
- theta浮点数数组,形状 (M,)
以度为单位的投影角度。不允许重复的角度。
- 返回:
- indices_generator生成器,产生无符号整数
返回的生成器产生
theta中的索引,使得theta[indices]给出投影的近似黄金比例排序。总共产生len(theta)个索引。所有非负整数 <len(theta)都被准确地产生一次。
注释
这里使用的方法是 T. Kohler 引入的黄金比例方法。
参考文献
[1]Kohler, T. “A projection access scheme for iterative reconstruction based on the golden section.” Nuclear Science Symposium Conference Record, 2004 IEEE. Vol. 6. IEEE, 2004.
[2]Winkelmann, Stefanie, et al. “An optimal radial profile order based on the Golden Ratio for time-resolved MRI.” Medical Imaging, IEEE Transactions on 26.1 (2007): 68-76.
- skimage.transform.probabilistic_hough_line(image, threshold=10, line_length=50, line_gap=10, theta=None, rng=None)[源代码]#
从渐进式概率线霍夫变换返回线。
- 参数:
- imagendarray,形状为 (M, N)
输入图像,非零值表示边缘。
- thresholdint,可选
阈值
- line_lengthint,可选
检测到的线的最小接受长度。增加参数以提取更长的线。
- line_gapint,可选
像素之间形成一条线的最大间隙。增加参数以更积极地合并断线。
- thetadtype 的 ndarray,形状 (K,),可选
计算变换的角度,以弧度为单位。默认为 180 个角度的向量,均匀分布在范围 [-pi/2, pi/2) 中。
- rng{
numpy.random.Generator, int}, 可选 伪随机数生成器。默认情况下,使用 PCG64 生成器(请参阅
numpy.random.default_rng())。如果rng是 int,则它用于为生成器设定种子。
- 返回:
- lines列表
已识别的线列表,线格式为 ((x0, y0), (x1, y1)),指示线的起点和终点。
参考文献
[1]C. Galamhos, J. Matas and J. Kittler, “Progressive probabilistic Hough transform for line detection”, in IEEE Computer Society Conference on Computer Vision and Pattern Recognition, 1999.
- skimage.transform.pyramid_expand(image, upscale=2, sigma=None, order=1, mode='reflect', cval=0, preserve_range=False, *, channel_axis=None)[源代码]#
上采样然后平滑图像。
- 参数:
- imagendarray
输入图像。
- upscalefloat,可选
放大系数。
- sigmafloat,可选
高斯滤波器的 Sigma 值。默认值为
2 * upscale / 6.0,这对应于比例因子的两倍大小的滤波器掩模,该掩模覆盖了高斯分布的 99% 以上。- orderint,可选
在对上采样进行插值时使用的样条曲线的阶数。有关详细信息,请参阅
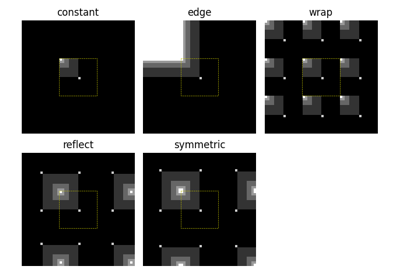
skimage.transform.warp。- mode{‘reflect’, ‘constant’, ‘edge’, ‘symmetric’, ‘wrap’}, 可选
mode 参数确定如何处理数组边界,其中 cval 是 mode 等于 ‘constant’ 时的值。
- cvalfloat,可选
如果 mode 为 ‘constant’,则填充输入边缘过去的值。
- preserve_rangebool,可选
是否保留原始值范围。 否则,将根据
img_as_float的约定转换输入图像。另请参阅 https://scikit-image.cn/docs/dev/user_guide/data_types.html- channel_axisint 或 None,可选
如果为 None,则假定图像为灰度(单通道)图像。否则,此参数指示数组的哪个轴对应于通道。
0.19 版本新增:
channel_axis在 0.19 版本中添加。
- 返回:
- out数组
上采样和平滑后的浮点图像。
参考文献
- skimage.transform.pyramid_gaussian(image, max_layer=-1, downscale=2, sigma=None, order=1, mode='reflect', cval=0, preserve_range=False, *, channel_axis=None)[源代码]#
生成输入图像形成的 Gaussian 金字塔的图像。
递归地将
pyramid_reduce函数应用于图像,并生成降采样后的图像。请注意,金字塔的第一张图像将是原始的、未缩放的图像。图像的总数为
max_layer + 1。如果计算所有层,则最后一张图像要么是单像素图像,要么是缩减不会改变其形状的图像。- 参数:
- imagendarray
输入图像。
- max_layerint, 可选
金字塔的层数。第 0 层是原始图像。默认值为 -1,表示构建所有可能的层。
- downscalefloat, 可选
降采样因子。
- sigmafloat,可选
高斯滤波器的 Sigma 值。默认值为
2 * downscale / 6.0,这对应于尺度因子的两倍大小的滤波器掩码,该掩码覆盖了高斯分布的 99% 以上。- orderint,可选
用于降采样插值的样条曲线阶数。有关详细信息,请参阅
skimage.transform.warp。- mode{‘reflect’, ‘constant’, ‘edge’, ‘symmetric’, ‘wrap’}, 可选
mode 参数确定如何处理数组边界,其中 cval 是 mode 等于 ‘constant’ 时的值。
- cvalfloat,可选
如果 mode 为 ‘constant’,则填充输入边缘过去的值。
- preserve_rangebool,可选
是否保留原始值范围。 否则,将根据
img_as_float的约定转换输入图像。另请参阅 https://scikit-image.cn/docs/dev/user_guide/data_types.html- channel_axisint 或 None,可选
如果为 None,则假定图像为灰度(单通道)图像。否则,此参数指示数组的哪个轴对应于通道。
0.19 版本新增:
channel_axis在 0.19 版本中添加。
- 返回:
- pyramid生成器
生成器,生成浮点图像的金字塔层。
参考文献
- skimage.transform.pyramid_laplacian(image, max_layer=-1, downscale=2, sigma=None, order=1, mode='reflect', cval=0, preserve_range=False, *, channel_axis=None)[源代码]#
生成输入图像形成的拉普拉斯金字塔的图像。
每一层都包含降采样图像与降采样平滑图像之间的差异
layer = resize(prev_layer) - smooth(resize(prev_layer))
请注意,金字塔的第一张图像将是原始、未缩放图像与其平滑版本之间的差异。图像的总数为
max_layer + 1。如果计算所有层,则最后一张图像要么是单像素图像,要么是缩减不会改变其形状的图像。- 参数:
- imagendarray
输入图像。
- max_layerint, 可选
金字塔的层数。第 0 层是原始图像。默认值为 -1,表示构建所有可能的层。
- downscalefloat, 可选
降采样因子。
- sigmafloat,可选
高斯滤波器的 Sigma 值。默认值为
2 * downscale / 6.0,这对应于尺度因子的两倍大小的滤波器掩码,该掩码覆盖了高斯分布的 99% 以上。- orderint,可选
用于降采样插值的样条曲线阶数。有关详细信息,请参阅
skimage.transform.warp。- mode{‘reflect’, ‘constant’, ‘edge’, ‘symmetric’, ‘wrap’}, 可选
mode 参数确定如何处理数组边界,其中 cval 是 mode 等于 ‘constant’ 时的值。
- cvalfloat,可选
如果 mode 为 ‘constant’,则填充输入边缘过去的值。
- preserve_rangebool,可选
是否保留原始值范围。 否则,将根据
img_as_float的约定转换输入图像。另请参阅 https://scikit-image.cn/docs/dev/user_guide/data_types.html- channel_axisint 或 None,可选
如果为 None,则假定图像为灰度(单通道)图像。否则,此参数指示数组的哪个轴对应于通道。
0.19 版本新增:
channel_axis在 0.19 版本中添加。
- 返回:
- pyramid生成器
生成器,生成浮点图像的金字塔层。
参考文献
- skimage.transform.pyramid_reduce(image, downscale=2, sigma=None, order=1, mode='reflect', cval=0, preserve_range=False, *, channel_axis=None)[源代码]#
平滑然后下采样图像。
- 参数:
- imagendarray
输入图像。
- downscalefloat, 可选
降采样因子。
- sigmafloat,可选
高斯滤波器的 Sigma 值。默认值为
2 * downscale / 6.0,这对应于尺度因子的两倍大小的滤波器掩码,该掩码覆盖了高斯分布的 99% 以上。- orderint,可选
用于降采样插值的样条曲线阶数。有关详细信息,请参阅
skimage.transform.warp。- mode{‘reflect’, ‘constant’, ‘edge’, ‘symmetric’, ‘wrap’}, 可选
mode 参数确定如何处理数组边界,其中 cval 是 mode 等于 ‘constant’ 时的值。
- cvalfloat,可选
如果 mode 为 ‘constant’,则填充输入边缘过去的值。
- preserve_rangebool,可选
是否保留原始值范围。 否则,将根据
img_as_float的约定转换输入图像。另请参阅 https://scikit-image.cn/docs/dev/user_guide/data_types.html- channel_axisint 或 None,可选
如果为 None,则假定图像为灰度(单通道)图像。否则,此参数指示数组的哪个轴对应于通道。
0.19 版本新增:
channel_axis在 0.19 版本中添加。
- 返回:
- out数组
平滑和降采样的浮点图像。
参考文献
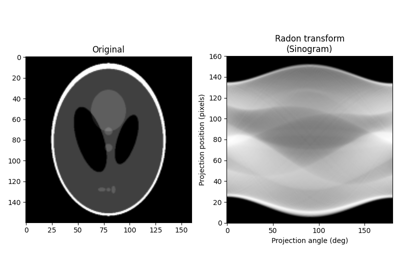
- skimage.transform.radon(image, theta=None, circle=True, *, preserve_range=False)[源代码]#
计算给定指定投影角度的图像的拉东变换。
- 参数:
- imagendarray
输入图像。旋转轴将位于索引为
(image.shape[0] // 2, image.shape[1] // 2)的像素中。- thetaarray,可选
投影角度(以度为单位)。如果为
None,则该值设置为 np.arange(180)。- circleboolean,可选
假设图像在内切圆之外为零,使每个投影的宽度(正弦图的第一个维度)等于
min(image.shape)。- preserve_rangebool,可选
是否保留原始值范围。 否则,将根据
img_as_float的约定转换输入图像。另请参阅 https://scikit-image.cn/docs/dev/user_guide/data_types.html
- 返回:
- radon_imagendarray
Radon 变换(正弦图)。断层扫描旋转轴将位于
radon_image的第 0 维的radon_image.shape[0] // 2像素索引处。
注释
基于 Justin K. Romberg 的代码 (https://www.clear.rice.edu/elec431/projects96/DSP/bpanalysis.html)
参考文献
[1]AC Kak, M Slaney, “Principles of Computerized Tomographic Imaging”, IEEE Press 1988.
[2]B.R. Ramesh, N. Srinivasa, K. Rajgopal, “An Algorithm for Computing the Discrete Radon Transform With Some Applications”, Proceedings of the Fourth IEEE Region 10 International Conference, TENCON ‘89, 1989
- skimage.transform.rescale(image, scale, order=None, mode='reflect', cval=0, clip=True, preserve_range=False, anti_aliasing=None, anti_aliasing_sigma=None, *, channel_axis=None)[源代码]#
按特定因子缩放图像。
执行插值以放大或缩小 N 维图像。请注意,在缩小图像以避免混叠伪影时,应启用抗锯齿。对于整数因子的降采样,另请参见
skimage.transform.downscale_local_mean。- 参数:
- image(M, N[, …][, C]) ndarray
输入图像。
- scale{float, float 元组}
空间维度的缩放因子。可以将单独的缩放因子定义为 (m, n[, …])。
- 返回:
- scaledndarray
输入图像的缩放版本。
- 其他参数:
- orderint,可选
样条插值的阶数,如果 image.dtype 是 bool 类型则默认为 0,否则默认为 1。阶数必须在 0-5 的范围内。详细信息请参阅
skimage.transform.warp。- mode{‘constant’, ‘edge’, ‘symmetric’, ‘reflect’, ‘wrap’}, 可选
输入图像边界外的点根据给定的模式进行填充。模式与
numpy.pad的行为匹配。- cvalfloat,可选
与模式 ‘constant’ 结合使用,表示图像边界外的值。
- clipbool,可选
是否将输出裁剪到输入图像的值范围内。默认启用此功能,因为高阶插值可能会产生超出给定输入范围的值。
- preserve_rangebool,可选
是否保留原始值范围。 否则,将根据
img_as_float的约定转换输入图像。另请参阅 https://scikit-image.cn/docs/dev/user_guide/data_types.html- anti_aliasingbool, 可选
是否在缩小图像之前应用高斯滤波器来平滑图像。在对图像进行降采样时,为了避免混叠伪影,进行滤波至关重要。如果输入图像的数据类型为 bool,则不应用抗锯齿。
- anti_aliasing_sigma{float, 浮点数元组}, 可选
用于高斯滤波以避免混叠伪影的标准偏差。默认情况下,此值选择为 (s - 1) / 2,其中 s 是降采样因子。
- channel_axisint 或 None,可选
如果为 None,则假定图像为灰度(单通道)图像。否则,此参数指示数组的哪个轴对应于通道。
0.19 版本新增:
channel_axis在 0.19 版本中添加。
注释
模式 ‘reflect’ 和 ‘symmetric’ 类似,但区别在于在反射期间是否复制边缘像素。例如,如果一个数组的值为 [0, 1, 2],并使用 symmetric 模式向右填充四个值,则结果将是 [0, 1, 2, 2, 1, 0, 0],而对于 reflect 模式,结果将是 [0, 1, 2, 1, 0, 1, 2]。
示例
>>> from skimage import data >>> from skimage.transform import rescale >>> image = data.camera() >>> rescale(image, 0.1).shape (51, 51) >>> rescale(image, 0.5).shape (256, 256)
- skimage.transform.resize(image, output_shape, order=None, mode='reflect', cval=0, clip=True, preserve_range=False, anti_aliasing=None, anti_aliasing_sigma=None)[源代码]#
调整图像大小以匹配特定大小。
执行插值以放大或缩小 N 维图像。请注意,在缩小图像时应启用抗锯齿以避免混叠伪影。对于整数因子的降采样,另请参阅
skimage.transform.downscale_local_mean。- 参数:
- imagendarray
输入图像。
- output_shape可迭代对象
生成的输出图像的大小
(行数, 列数[, ...][, 维度])。如果未提供维度,则保留通道数。如果输入通道数不等于输出通道数,则应用 n 维插值。
- 返回:
- resizedndarray
输入图像的调整大小版本。
- 其他参数:
- orderint,可选
样条插值的阶数,如果 image.dtype 是 bool 类型则默认为 0,否则默认为 1。阶数必须在 0-5 的范围内。详细信息请参阅
skimage.transform.warp。- mode{‘constant’, ‘edge’, ‘symmetric’, ‘reflect’, ‘wrap’}, 可选
输入图像边界外的点根据给定的模式进行填充。模式与
numpy.pad的行为匹配。- cvalfloat,可选
与模式 ‘constant’ 结合使用,表示图像边界外的值。
- clipbool,可选
是否将输出裁剪到输入图像的值范围内。默认启用此功能,因为高阶插值可能会产生超出给定输入范围的值。
- preserve_rangebool,可选
是否保留原始值范围。 否则,将根据
img_as_float的约定转换输入图像。另请参阅 https://scikit-image.cn/docs/dev/user_guide/data_types.html- anti_aliasingbool, 可选
是否在降采样之前应用高斯滤波器来平滑图像。在对图像进行降采样时,为了避免混叠伪影,进行滤波至关重要。如果未指定,则在降采样数据类型不是 bool 的图像时,它设置为 True。当使用最近邻插值 (
order== 0) 且输入数据类型为整数时,它也会设置为 False。- anti_aliasing_sigma{float, 浮点数元组}, 可选
用于抗锯齿时的高斯滤波标准差。默认情况下,此值选择为 (s - 1) / 2,其中 s 是降采样因子,且 s > 1。对于放大情况,s < 1,在重新缩放之前不执行抗锯齿。
注释
模式 ‘reflect’ 和 ‘symmetric’ 类似,但区别在于在反射期间是否复制边缘像素。例如,如果一个数组的值为 [0, 1, 2],并使用 symmetric 模式向右填充四个值,则结果将是 [0, 1, 2, 2, 1, 0, 0],而对于 reflect 模式,结果将是 [0, 1, 2, 1, 0, 1, 2]。
示例
>>> from skimage import data >>> from skimage.transform import resize >>> image = data.camera() >>> resize(image, (100, 100)).shape (100, 100)
- skimage.transform.resize_local_mean(image, output_shape, grid_mode=True, preserve_range=False, *, channel_axis=None)[源代码]#
使用局部均值/双线性缩放调整数组大小。
- 参数:
- imagendarray
输入图像。如果这是一个多通道图像,则应使用
channel_axis指定对应于通道的轴。- output_shape可迭代对象
生成的输出图像的大小。当
channel_axis不为 None 时,channel_axis应从output_shape中省略,或者output_shape[channel_axis]必须与image.shape[channel_axis]匹配。如果output_shape的长度超过 image.ndim,则根据需要将额外的单例维度附加到输入image。- grid_modebool, 可选
定义
image像素的位置:如果为 True,则假定像素位于网格交叉点处,否则位于单元格中心。因此,例如,当grid_mode为 False 时,长度为 5 的一维信号被认为长度为 4,但当grid_mode为 True 时,长度为 5。请参见以下视觉插图| pixel 1 | pixel 2 | pixel 3 | pixel 4 | pixel 5 | |<-------------------------------------->| vs. |<----------------------------------------------->|上图中箭头的起点对应于每种模式下的坐标位置 0。
- preserve_rangebool,可选
是否保留原始值范围。 否则,将根据
img_as_float的约定转换输入图像。另请参阅 https://scikit-image.cn/docs/dev/user_guide/data_types.html
- 返回:
- resizedndarray
输入图像的调整大小版本。
另请参阅
注释
此方法有时被称为“基于区域”的插值或“像素混合”插值 [1]。当
grid_mode为 True 时,它等效于使用 OpenCV 的INTER_AREA插值模式进行调整大小。它通常用于图像缩小。如果缩小因子是整数,则应首选downscale_local_mean。参考文献
示例
>>> from skimage import data >>> from skimage.transform import resize_local_mean >>> image = data.camera() >>> resize_local_mean(image, (100, 100)).shape (100, 100)
- skimage.transform.rotate(image, angle, resize=False, center=None, order=None, mode='constant', cval=0, clip=True, preserve_range=False)[源代码]#
围绕中心将图像旋转特定角度。
- 参数:
- imagendarray
输入图像。
- anglefloat
以逆时针方向旋转的角度(度)。
- resizebool, 可选
确定是否自动计算输出图像的形状,以便完整旋转的图像完全适合。默认为 False。
- center长度为 2 的可迭代对象
旋转中心。如果
center=None,则图像绕其中心旋转,即center=(列数 / 2 - 0.5, 行数 / 2 - 0.5)。请注意,此参数为 (列数, 行数),与正常的 skimage 顺序相反。
- 返回:
- 旋转后的ndarray
输入图像的旋转版本。
- 其他参数:
- orderint,可选
样条插值的阶数,如果 image.dtype 是 bool 类型则默认为 0,否则默认为 1。阶数必须在 0-5 的范围内。详细信息请参阅
skimage.transform.warp。- mode{‘constant’, ‘edge’, ‘symmetric’, ‘reflect’, ‘wrap’}, 可选
输入图像边界外的点根据给定的模式进行填充。模式与
numpy.pad的行为匹配。- cvalfloat,可选
与模式 ‘constant’ 结合使用,表示图像边界外的值。
- clipbool,可选
是否将输出裁剪到输入图像的值范围内。默认启用此功能,因为高阶插值可能会产生超出给定输入范围的值。
- preserve_rangebool,可选
是否保留原始值范围。 否则,将根据
img_as_float的约定转换输入图像。另请参阅 https://scikit-image.cn/docs/dev/user_guide/data_types.html
注释
模式 ‘reflect’ 和 ‘symmetric’ 类似,但区别在于在反射期间是否复制边缘像素。例如,如果一个数组的值为 [0, 1, 2],并使用 symmetric 模式向右填充四个值,则结果将是 [0, 1, 2, 2, 1, 0, 0],而对于 reflect 模式,结果将是 [0, 1, 2, 1, 0, 1, 2]。
示例
>>> from skimage import data >>> from skimage.transform import rotate >>> image = data.camera() >>> rotate(image, 2).shape (512, 512) >>> rotate(image, 2, resize=True).shape (530, 530) >>> rotate(image, 90, resize=True).shape (512, 512)
- skimage.transform.swirl(image, center=None, strength=1, radius=100, rotation=0, output_shape=None, order=None, mode='reflect', cval=0, clip=True, preserve_range=False)[source]#
执行漩涡变换。
- 参数:
- imagendarray
输入图像。
- center(列, 行) 元组或 (2,) ndarray,可选
变换的中心坐标。
- strengthfloat,可选
应用的漩涡量。
- radiusfloat,可选
漩涡的范围(以像素为单位)。效果在
radius之外迅速消失。- rotationfloat,可选
应用于图像的额外旋转。
- 返回:
- swirledndarray
输入图像的漩涡版本。
- 其他参数:
- output_shape元组 (rows, cols),可选
生成的输出图像的形状。默认情况下,保留输入图像的形状。
- orderint,可选
样条插值的阶数,如果 image.dtype 是 bool 类型则默认为 0,否则默认为 1。阶数必须在 0-5 的范围内。详细信息请参阅
skimage.transform.warp。- mode{‘constant’, ‘edge’, ‘symmetric’, ‘reflect’, ‘wrap’}, 可选
根据给定的模式填充输入边界之外的点,默认使用“reflect”。模式与
numpy.pad的行为一致。- cvalfloat,可选
与模式 ‘constant’ 结合使用,表示图像边界外的值。
- clipbool,可选
是否将输出裁剪到输入图像的值范围内。默认启用此功能,因为高阶插值可能会产生超出给定输入范围的值。
- preserve_rangebool,可选
是否保留原始值范围。 否则,将根据
img_as_float的约定转换输入图像。另请参阅 https://scikit-image.cn/docs/dev/user_guide/data_types.html
- skimage.transform.warp(image, inverse_map, map_args=None, output_shape=None, order=None, mode='constant', cval=0.0, clip=True, preserve_range=False)[source]#
根据给定的坐标变换扭曲图像。
- 参数:
- imagendarray
输入图像。
- inverse_map变换对象,可调用
cr = f(cr, **kwargs),或 ndarray 逆坐标映射,将输出图像中的坐标转换为输入图像中的相应坐标。
定义此映射有多种不同的选项,具体取决于输入图像的维度。2D 图像可以是灰度图像的 2 个维度,也可以是具有颜色信息的 3 个维度。
对于 2D 图像,您可以直接传递变换对象,例如
skimage.transform.SimilarityTransform,或其逆变换。对于 2D 图像,您可以传递
(3, 3)齐次变换矩阵,例如skimage.transform.SimilarityTransform.params。对于 2D 图像,可以使用函数将输出图像中
(M, 2)的(col, row)坐标数组转换为输入图像中的相应坐标。可以通过map_args指定函数的额外参数。对于 N-D 图像,您可以直接传递坐标数组。第一个维度指定输入图像中的坐标,而后续维度确定输出图像中的位置。例如,对于 2D 图像,您需要传递一个形状为
(2, rows, cols)的数组,其中rows和cols确定输出图像的形状,并且第一个维度包含输入图像中的(row, col)坐标。有关更多文档,请参见scipy.ndimage.map_coordinates。
请注意,
(3, 3)矩阵被解释为齐次变换矩阵,因此如果输出的形状为(3,),则无法从 3D 输入插值。有关用法,请参见示例部分。
- map_argsdict,可选
传递给
inverse_map的关键字参数。- output_shape元组 (rows, cols),可选
生成的输出图像的形状。默认情况下,保留输入图像的形状。请注意,即使对于多波段图像,也只需要指定行和列。
- orderint,可选
- 插值顺序。顺序必须在 0-5 的范围内
0:最近邻
1:双线性(默认)
2:双二次
3:双三次
4:双四次
5:双五次
如果 image.dtype 为 bool,则默认为 0,否则为 1。
- mode{‘constant’, ‘edge’, ‘symmetric’, ‘reflect’, ‘wrap’}, 可选
输入图像边界外的点根据给定的模式进行填充。模式与
numpy.pad的行为匹配。- cvalfloat,可选
与模式 ‘constant’ 结合使用,表示图像边界外的值。
- clipbool,可选
是否将输出裁剪到输入图像的值范围内。默认启用此功能,因为高阶插值可能会产生超出给定输入范围的值。
- preserve_rangebool,可选
是否保留原始值范围。 否则,将根据
img_as_float的约定转换输入图像。另请参阅 https://scikit-image.cn/docs/dev/user_guide/data_types.html
- 返回:
- warpeddouble ndarray
扭曲的输入图像。
注释
输入图像被转换为
double图像。对于
SimilarityTransform、AffineTransform和ProjectiveTransform且order在 [0, 3] 中,此函数使用底层变换矩阵通过更快的例程来扭曲图像。
示例
>>> from skimage.transform import warp >>> from skimage import data >>> image = data.camera()
以下图像扭曲都相等,但在执行时间上差异很大。图像移动到底部。
使用几何变换来扭曲图像(快速)
>>> from skimage.transform import SimilarityTransform >>> tform = SimilarityTransform(translation=(0, -10)) >>> warped = warp(image, tform)
使用可调用对象(慢)
>>> def shift_down(xy): ... xy[:, 1] -= 10 ... return xy >>> warped = warp(image, shift_down)
使用变换矩阵来扭曲图像(快速)
>>> matrix = np.array([[1, 0, 0], [0, 1, -10], [0, 0, 1]]) >>> warped = warp(image, matrix) >>> from skimage.transform import ProjectiveTransform >>> warped = warp(image, ProjectiveTransform(matrix=matrix))
您还可以使用几何变换的逆变换(快速)
>>> warped = warp(image, tform.inverse)
对于 N-D 图像,您可以传递一个坐标数组,该数组指定输出图像中每个元素的输入图像中的坐标。例如,如果您要重新缩放 3D 立方体,您可以执行
>>> cube_shape = np.array([30, 30, 30]) >>> rng = np.random.default_rng() >>> cube = rng.random(cube_shape)
设置定义缩放的坐标数组
>>> scale = 0.1 >>> output_shape = (scale * cube_shape).astype(int) >>> coords0, coords1, coords2 = np.mgrid[:output_shape[0], ... :output_shape[1], :output_shape[2]] >>> coords = np.array([coords0, coords1, coords2])
假设立方体包含空间数据,其中第一个数组元素的中心位于实际空间中的坐标 (0.5, 0.5, 0.5),即在缩放图像时我们必须考虑这个额外的偏移量
>>> coords = (coords + 0.5) / scale - 0.5 >>> warped = warp(cube, coords)
- skimage.transform.warp_coords(coord_map, shape, dtype=<class 'numpy.float64'>)[source]#
为 2-D 图像扭曲的输出构建源坐标。
- 参数:
- coord_map类似于 GeometricTransform.inverse 的可调用对象
返回给定输出坐标的输入坐标。坐标的形状为 (P, 2),其中 P 是坐标数,并且每个元素都是一个
(row, col)对。- shape元组
输出图像的形状
(rows, cols[, bands])。- dtypenp.dtype 或字符串
返回值的数据类型(合理的选择:float32 或 float64)。
- 返回:
- coords(ndim, rows, cols[, bands]) 数据类型为
dtype的数组 scipy.ndimage.map_coordinates的坐标,它将通过根据coord_transform_fn从源点绘制,生成形状为 (orows, ocols, bands) 的图像。
- coords(ndim, rows, cols[, bands]) 数据类型为
注释
这是一个较低级的例程,用于生成
warp()使用的 2-D 图像的源坐标。它与
warp分开提供,以便为希望例如重用特定坐标映射、在图像扭曲过程的各个点使用特定数据类型,或实现与warp在调用ndi.map_coordinates后执行的不同的后处理逻辑的用户提供额外的灵活性。示例
生成一个坐标映射,将图像向上和向右移动
>>> from skimage import data >>> from scipy.ndimage import map_coordinates >>> >>> def shift_up10_left20(xy): ... return xy - np.array([-20, 10])[None, :] >>> >>> image = data.astronaut().astype(np.float32) >>> coords = warp_coords(shift_up10_left20, image.shape) >>> warped_image = map_coordinates(image, coords)
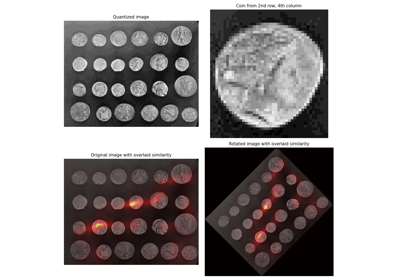
- skimage.transform.warp_polar(image, center=None, *, radius=None, output_shape=None, scaling='linear', channel_axis=None, **kwargs)[源代码]#
将图像重新映射到极坐标或对数极坐标空间。
- 参数:
- image(M, N[, C]) ndarray
输入图像。对于多通道图像,必须指定
channel_axis。- center2 元组,可选
(行, 列)在image中表示变换中心的点的坐标(即,笛卡尔空间中的原点)。值可以是float类型。如果未提供值,则假设中心是image的中心点。- radiusfloat,可选
包围要变换的区域的圆的半径。
- output_shape元组 (行, 列), 可选
- scaling{‘linear’, ‘log’}, 可选
指定图像扭曲是极坐标还是对数极坐标。默认为 ‘linear’。
- channel_axisint 或 None,可选
如果为 None,则假定图像为灰度(单通道)图像。否则,此参数指示数组的哪个轴对应于通道。
0.19 版本新增:
channel_axis在 0.19 版本中添加。- **kwargs关键字参数
传递给
transform.warp。
- 返回:
- warpedndarray
极坐标或对数极坐标扭曲的图像。
示例
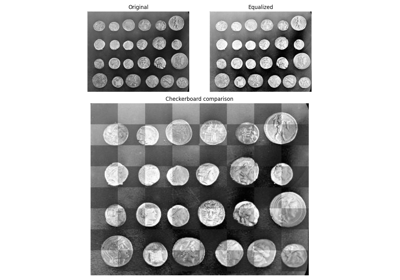
对灰度图像执行基本的极坐标扭曲
>>> from skimage import data >>> from skimage.transform import warp_polar >>> image = data.checkerboard() >>> warped = warp_polar(image)
对灰度图像执行对数极坐标扭曲
>>> warped = warp_polar(image, scaling='log')
在指定中心、半径和输出形状的同时对灰度图像执行对数极坐标扭曲
>>> warped = warp_polar(image, (100,100), radius=100, ... output_shape=image.shape, scaling='log')
对彩色图像执行对数极坐标扭曲
>>> image = data.astronaut() >>> warped = warp_polar(image, scaling='log', channel_axis=-1)
- class skimage.transform.AffineTransform(matrix=None, scale=None, rotation=None, shear=None, translation=None, *, dimensionality=2)[源代码]#
-
仿射变换。
具有以下形式
X = a0 * x + a1 * y + a2 = sx * x * [cos(rotation) + tan(shear_y) * sin(rotation)] - sy * y * [tan(shear_x) * cos(rotation) + sin(rotation)] + translation_x Y = b0 * x + b1 * y + b2 = sx * x * [sin(rotation) - tan(shear_y) * cos(rotation)] - sy * y * [tan(shear_x) * sin(rotation) - cos(rotation)] + translation_y
其中
sx和sy是 x 和 y 方向上的比例因子。这相当于按以下顺序应用操作
缩放
剪切
旋转
平移
齐次变换矩阵是
[[a0 a1 a2] [b0 b1 b2] [0 0 1]]
在 2D 中,变换参数可以作为齐次变换矩阵(如上所示)给出,也可以作为隐式参数(x (a2) 和 y (b2) 中的比例、旋转、剪切和平移)给出。对于 3D 和更高维度,只允许矩阵形式。
在较窄的变换中,例如欧几里得变换(仅旋转和平移)或相似变换(旋转、平移和全局比例因子),也可以使用隐式参数指定 3D 变换。
- 参数:
- matrix(D+1, D+1) 类似数组, 可选
齐次变换矩阵。如果提供了此矩阵,则提供任何比例、旋转、剪切或平移参数都是错误的。
- scale{s 为 float 或 (sx, sy) 为数组、列表或元组}, 可选
比例因子。如果为单个值,则将同时分配给 sx 和 sy。仅适用于 2D。
0.17 版本中新增:添加了对提供单个标量值的支持。
- rotationfloat,可选
旋转角度,顺时针方向,以弧度为单位。仅适用于 2D。
- shearfloat 或 2 元组 float, 可选
x 和 y 剪切角,顺时针方向,这些轴围绕原点旋转 [2]。如果给出一个值,则将其视为 x 剪切角,y 角保持为 0。仅适用于 2D。
- translation(tx, ty) 为数组、列表或元组, 可选
平移参数。仅适用于 2D。
- dimensionalityint, 可选
变换的维度。如果提供了任何其他参数,则不使用此参数。
- 属性:
- params(D+1, D+1) 数组
齐次变换矩阵。
- 引发:
- ValueError
如果同时提供了
matrix和任何其他参数。
参考文献
[2]维基百科,“剪切映射”,https://en.wikipedia.org/wiki/Shear_mapping
示例
>>> import numpy as np >>> import skimage as ski >>> img = ski.data.astronaut()
定义源点和目标点
>>> src = np.array([[150, 150], ... [250, 100], ... [150, 200]]) >>> dst = np.array([[200, 200], ... [300, 150], ... [150, 400]])
估计变换矩阵
>>> tform = ski.transform.AffineTransform() >>> tform.estimate(src, dst) True
应用变换
>>> warped = ski.transform.warp(img, inverse_map=tform.inverse)
- __init__(matrix=None, scale=None, rotation=None, shear=None, translation=None, *, dimensionality=2)[源代码]#
- property dimensionality#
变换的维度。
- estimate(src, dst, weights=None)[源代码]#
从一组对应的点估计变换。
您可以使用总最小二乘法确定过度、良好和欠定的参数。
源坐标和目标坐标的数量必须匹配。
变换定义为
X = (a0*x + a1*y + a2) / (c0*x + c1*y + 1) Y = (b0*x + b1*y + b2) / (c0*x + c1*y + 1)
这些方程可以变换为以下形式
0 = a0*x + a1*y + a2 - c0*x*X - c1*y*X - X 0 = b0*x + b1*y + b2 - c0*x*Y - c1*y*Y - Y
对于每一组对应的点都存在这种情况,因此我们有一组 N * 2 个方程。系数线性出现,因此我们可以写成 A x = 0,其中
A = [[x y 1 0 0 0 -x*X -y*X -X] [0 0 0 x y 1 -x*Y -y*Y -Y] ... ... ] x.T = [a0 a1 a2 b0 b1 b2 c0 c1 c3]
在总体最小二乘法的情况下,该齐次方程组的解是 A 的右奇异向量,它对应于按系数 c3 规范化的最小奇异值。
权重可以应用于每对对应的点,以指示(特别是在超定系统中)点对是否具有较高或较低的置信度或与之相关的不确定性。根据最小二乘问题的矩阵处理,这些权重值被归一化、开平方根,然后构建到一个对角矩阵中,A 与该矩阵相乘。
在仿射变换的情况下,系数 c0 和 c1 为 0。因此方程组为
A = [[x y 1 0 0 0 -X] [0 0 0 x y 1 -Y] ... ... ] x.T = [a0 a1 a2 b0 b1 b2 c3]
- 参数:
- src(N, 2) 类似数组
源坐标。
- dst(N, 2) 类似数组
目标坐标。
- weights(N,) 类似数组, 可选
每对点的相对权重值。
- 返回:
- successbool
如果模型估计成功,则为 True。
- 属性 inverse#
返回一个表示逆变换的变换对象。
- residuals(src, dst)[源代码]#
确定变换后的目标坐标的残差。
对于每个变换后的源坐标,确定其到相应目标坐标的欧几里得距离。
- 参数:
- src(N, 2) 数组
源坐标。
- dst(N, 2) 数组
目标坐标。
- 返回:
- residuals(N,) 数组
坐标的残差。
- 属性 rotation#
- 属性 scale#
- 属性 shear#
- 属性 translation#
- 类 skimage.transform.EssentialMatrixTransform(rotation=None, translation=None, matrix=None, *, dimensionality=2)[源代码]#
基类:
FundamentalMatrixTransform基本矩阵变换。
本质矩阵关联一对已校准图像之间的对应点。该矩阵将一个图像中的归一化齐次图像点变换为另一个图像中的外极线。
本质矩阵仅为捕获非平面场景的一对移动图像定义。在纯旋转或平面场景的情况下,单应性描述两个图像之间的几何关系 (
ProjectiveTransform)。如果图像的内在校准未知,则基础矩阵描述两个图像之间的投影关系 (FundamentalMatrixTransform)。- 参数:
- rotation(3, 3) 类似数组, 可选
相对相机运动的旋转矩阵。
- translation(3, 1) 类似数组, 可选
相对相机运动的平移向量。该向量必须具有单位长度。
- matrix(3, 3) 类似数组, 可选
本质矩阵。
- 属性:
- params(3, 3) 数组
本质矩阵。
参考文献
[1]Hartley, Richard, and Andrew Zisserman. 计算机视觉中的多视图几何。剑桥大学出版社,2003 年。
示例
>>> import numpy as np >>> import skimage as ski >>> >>> tform_matrix = ski.transform.EssentialMatrixTransform( ... rotation=np.eye(3), translation=np.array([0, 0, 1]) ... ) >>> tform_matrix.params array([[ 0., -1., 0.], [ 1., 0., 0.], [ 0., 0., 0.]]) >>> src = np.array([[ 1.839035, 1.924743], ... [ 0.543582, 0.375221], ... [ 0.47324 , 0.142522], ... [ 0.96491 , 0.598376], ... [ 0.102388, 0.140092], ... [15.994343, 9.622164], ... [ 0.285901, 0.430055], ... [ 0.09115 , 0.254594]]) >>> dst = np.array([[1.002114, 1.129644], ... [1.521742, 1.846002], ... [1.084332, 0.275134], ... [0.293328, 0.588992], ... [0.839509, 0.08729 ], ... [1.779735, 1.116857], ... [0.878616, 0.602447], ... [0.642616, 1.028681]]) >>> tform_matrix.estimate(src, dst) True >>> tform_matrix.residuals(src, dst) array([0.42455187, 0.01460448, 0.13847034, 0.12140951, 0.27759346, 0.32453118, 0.00210776, 0.26512283])
- estimate(src, dst)[源代码]#
使用 8 点算法估计本质矩阵。
8 点算法至少需要 8 个对应的点对才能得到条件良好的解,否则将估计过度确定的解。
- 参数:
- src(N, 2) 类似数组
源坐标。
- dst(N, 2) 类似数组
目标坐标。
- 返回:
- successbool
如果模型估计成功,则为 True。
- 属性 inverse#
返回一个表示逆变换的变换对象。
有关为什么 F.T 给出逆矩阵的解释,请参阅 Hartley 和 Zisserman 的第 8 章:外极几何和基础矩阵。
- 类 skimage.transform.EuclideanTransform(matrix=None, rotation=None, translation=None, *, dimensionality=2)[源代码]#
-
欧几里得变换,也称为刚性变换。
具有以下形式
X = a0 * x - b0 * y + a1 = = x * cos(rotation) - y * sin(rotation) + a1 Y = b0 * x + a0 * y + b1 = = x * sin(rotation) + y * cos(rotation) + b1
其中齐次变换矩阵为
[[a0 -b0 a1] [b0 a0 b1] [0 0 1 ]]
欧几里得变换是具有旋转和平移参数的刚性变换。相似变换通过单个缩放因子扩展了欧几里得变换。
在 2D 和 3D 中,变换参数可以通过上述齐次变换矩阵
matrix提供,也可以通过隐式参数rotation和/或translation提供(其中a1是沿x的平移,b1是沿y的平移,等等)。在 3D 以上,如果变换只是平移,则可以使用隐式参数translation;否则,必须使用matrix。- 参数:
- matrix(D+1, D+1) 类似数组, 可选
齐次变换矩阵。
- rotation浮点数或浮点数序列, 可选
旋转角度,顺时针,以弧度为单位。如果以向量形式给出,则将其解释为欧拉旋转角 [1]。仅支持 2D(单次旋转)和 3D(欧拉旋转)值。对于更高维度,您必须提供或估计变换矩阵。
- translation(x, y[, z, …]) 浮点数序列, 长度为 D, 可选
每个轴的平移参数。
- dimensionalityint, 可选
变换的维度。
- 属性:
- params(D+1, D+1) 数组
齐次变换矩阵。
参考文献
- property dimensionality#
变换的维度。
- estimate(src, dst)[source]#
从一组对应的点估计变换。
您可以使用总最小二乘法确定过度、良好和欠定的参数。
源坐标和目标坐标的数量必须匹配。
- 参数:
- src(N, 2) 类似数组
源坐标。
- dst(N, 2) 类似数组
目标坐标。
- 返回:
- successbool
如果模型估计成功,则为 True。
- property inverse#
返回一个表示逆变换的变换对象。
- residuals(src, dst)[source]#
确定变换后的目标坐标的残差。
对于每个变换后的源坐标,确定其到相应目标坐标的欧几里得距离。
- 参数:
- src(N, 2) 数组
源坐标。
- dst(N, 2) 数组
目标坐标。
- 返回:
- residuals(N,) 数组
坐标的残差。
- property rotation#
- property translation#
- class skimage.transform.FundamentalMatrixTransform(matrix=None, *, dimensionality=2)[source]#
基类:
_GeometricTransform基本矩阵变换。
基础矩阵关联一对未校准图像之间的对应点。该矩阵将一个图像中的齐次图像点转换为另一图像中的外极线。
基础矩阵仅针对一对移动图像定义。在纯旋转或平面场景的情况下,单应性描述了两个图像之间的几何关系(
ProjectiveTransform)。如果已知图像的内部校准,则本质矩阵描述了两个图像之间的度量关系(EssentialMatrixTransform)。- 参数:
- matrix(3, 3) 类似数组, 可选
基础矩阵。
- 属性:
- params(3, 3) 数组
基础矩阵。
参考文献
[1]Hartley, Richard, and Andrew Zisserman. 计算机视觉中的多视图几何。剑桥大学出版社,2003 年。
示例
>>> import numpy as np >>> import skimage as ski >>> tform_matrix = ski.transform.FundamentalMatrixTransform()
定义源点和目标点
>>> src = np.array([1.839035, 1.924743, ... 0.543582, 0.375221, ... 0.473240, 0.142522, ... 0.964910, 0.598376, ... 0.102388, 0.140092, ... 15.994343, 9.622164, ... 0.285901, 0.430055, ... 0.091150, 0.254594]).reshape(-1, 2) >>> dst = np.array([1.002114, 1.129644, ... 1.521742, 1.846002, ... 1.084332, 0.275134, ... 0.293328, 0.588992, ... 0.839509, 0.087290, ... 1.779735, 1.116857, ... 0.878616, 0.602447, ... 0.642616, 1.028681]).reshape(-1, 2)
估计变换矩阵
>>> tform_matrix.estimate(src, dst) True >>> tform_matrix.params array([[-0.21785884, 0.41928191, -0.03430748], [-0.07179414, 0.04516432, 0.02160726], [ 0.24806211, -0.42947814, 0.02210191]])
计算 Sampson 距离
>>> tform_matrix.residuals(src, dst) array([0.0053886 , 0.00526101, 0.08689701, 0.01850534, 0.09418259, 0.00185967, 0.06160489, 0.02655136])
应用逆变换
>>> tform_matrix.inverse(dst) array([[-0.0513591 , 0.04170974, 0.01213043], [-0.21599496, 0.29193419, 0.00978184], [-0.0079222 , 0.03758889, -0.00915389], [ 0.14187184, -0.27988959, 0.02476507], [ 0.05890075, -0.07354481, -0.00481342], [-0.21985267, 0.36717464, -0.01482408], [ 0.01339569, -0.03388123, 0.00497605], [ 0.03420927, -0.1135812 , 0.02228236]])
- estimate(src, dst)[source]#
使用 8 点算法估计基础矩阵。
8 点算法至少需要 8 个对应的点对才能得到条件良好的解,否则将估计过度确定的解。
- 参数:
- src(N, 2) 类似数组
源坐标。
- dst(N, 2) 类似数组
目标坐标。
- 返回:
- successbool
如果模型估计成功,则为 True。
- property inverse#
返回一个表示逆变换的变换对象。
有关为什么 F.T 给出逆矩阵的解释,请参阅 Hartley 和 Zisserman 的第 8 章:外极几何和基础矩阵。
- class skimage.transform.PiecewiseAffineTransform[source]#
基类:
_GeometricTransform分段仿射变换。
控制点用于定义映射。该变换基于点的 Delaunay 三角剖分形成网格。每个三角形用于查找局部仿射变换。
- 属性:
- affines仿射变换对象列表
网格中每个三角形的仿射变换。
- inverse_affines仿射变换对象列表
网格中每个三角形的逆仿射变换。
- estimate(src, dst)[source]#
从一组对应的点估计变换。
源坐标和目标坐标的数量必须匹配。
- 参数:
- src(N, D) 类数组
源坐标。
- dst(N, D) 类数组
目标坐标。
- 返回:
- successbool
如果模型的所有部分都已成功估计,则为 True。
- property inverse#
返回一个表示逆变换的变换对象。
- class skimage.transform.PolynomialTransform(params=None, *, dimensionality=2)[source]#
基类:
_GeometricTransform2D 多项式变换。
具有以下形式
X = sum[j=0:order]( sum[i=0:j]( a_ji * x**(j - i) * y**i )) Y = sum[j=0:order]( sum[i=0:j]( b_ji * x**(j - i) * y**i ))
- 参数:
- params(2, N) 类数组,可选
多项式系数,其中
N * 2 = (order + 1) * (order + 2)。因此,a_ji 在params[0, :]中定义,而 b_ji 在params[1, :]中定义。
- 属性:
- params(2, N) 数组
多项式系数,其中
N * 2 = (order + 1) * (order + 2)。因此,a_ji 在params[0, :]中定义,而 b_ji 在params[1, :]中定义。
- estimate(src, dst, order=2, weights=None)[source]#
从一组对应的点估计变换。
您可以使用总最小二乘法确定过度、良好和欠定的参数。
源坐标和目标坐标的数量必须匹配。
变换定义为
X = sum[j=0:order]( sum[i=0:j]( a_ji * x**(j - i) * y**i )) Y = sum[j=0:order]( sum[i=0:j]( b_ji * x**(j - i) * y**i ))
这些方程可以变换为以下形式
0 = sum[j=0:order]( sum[i=0:j]( a_ji * x**(j - i) * y**i )) - X 0 = sum[j=0:order]( sum[i=0:j]( b_ji * x**(j - i) * y**i )) - Y
对于每一组对应的点都存在这种情况,因此我们有一组 N * 2 个方程。系数线性出现,因此我们可以写成 A x = 0,其中
A = [[1 x y x**2 x*y y**2 ... 0 ... 0 -X] [0 ... 0 1 x y x**2 x*y y**2 -Y] ... ... ] x.T = [a00 a10 a11 a20 a21 a22 ... ann b00 b10 b11 b20 b21 b22 ... bnn c3]
在总体最小二乘法的情况下,该齐次方程组的解是 A 的右奇异向量,它对应于按系数 c3 规范化的最小奇异值。
权重可以应用于每对对应的点,以指示(特别是在超定系统中)点对是否具有较高或较低的置信度或与之相关的不确定性。根据最小二乘问题的矩阵处理,这些权重值被归一化、开平方根,然后构建到一个对角矩阵中,A 与该矩阵相乘。
- 参数:
- src(N, 2) 类似数组
源坐标。
- dst(N, 2) 类似数组
目标坐标。
- orderint,可选
多项式阶数(系数的数量是阶数 + 1)。
- weights(N,) 类似数组, 可选
每对点的相对权重值。
- 返回:
- successbool
如果模型估计成功,则为 True。
- 属性 inverse#
返回一个表示逆变换的变换对象。
- class skimage.transform.ProjectiveTransform(matrix=None, *, dimensionality=2)[source]#
基类:
_GeometricTransform透视变换。
在坐标上应用投影变换(单应性)。
对于每个齐次坐标 \(\mathbf{x} = [x, y, 1]^T\),其目标位置通过与给定矩阵 \(H\) 相乘来计算,得到 \(H \mathbf{x}\)
[[a0 a1 a2] [b0 b1 b2] [c0 c1 1 ]].
例如,要顺时针旋转 theta 度,矩阵应为
[[cos(theta) -sin(theta) 0] [sin(theta) cos(theta) 0] [0 0 1]]
或者,将 x 平移 10,将 y 平移 20
[[1 0 10] [0 1 20] [0 0 1 ]].
- 参数:
- matrix(D+1, D+1) 类似数组, 可选
齐次变换矩阵。
- dimensionalityint, 可选
变换的维度数。如果
matrix不为 None,则忽略此项。
- 属性:
- params(D+1, D+1) 数组
齐次变换矩阵。
- 属性 dimensionality#
变换的维度。
- estimate(src, dst, weights=None)[source]#
从一组对应的点估计变换。
您可以使用总最小二乘法确定过度、良好和欠定的参数。
源坐标和目标坐标的数量必须匹配。
变换定义为
X = (a0*x + a1*y + a2) / (c0*x + c1*y + 1) Y = (b0*x + b1*y + b2) / (c0*x + c1*y + 1)
这些方程可以变换为以下形式
0 = a0*x + a1*y + a2 - c0*x*X - c1*y*X - X 0 = b0*x + b1*y + b2 - c0*x*Y - c1*y*Y - Y
对于每一组对应的点都存在这种情况,因此我们有一组 N * 2 个方程。系数线性出现,因此我们可以写成 A x = 0,其中
A = [[x y 1 0 0 0 -x*X -y*X -X] [0 0 0 x y 1 -x*Y -y*Y -Y] ... ... ] x.T = [a0 a1 a2 b0 b1 b2 c0 c1 c3]
在总体最小二乘法的情况下,该齐次方程组的解是 A 的右奇异向量,它对应于按系数 c3 规范化的最小奇异值。
权重可以应用于每对对应的点,以指示(特别是在超定系统中)点对是否具有较高或较低的置信度或与之相关的不确定性。根据最小二乘问题的矩阵处理,这些权重值被归一化、开平方根,然后构建到一个对角矩阵中,A 与该矩阵相乘。
在仿射变换的情况下,系数 c0 和 c1 为 0。因此方程组为
A = [[x y 1 0 0 0 -X] [0 0 0 x y 1 -Y] ... ... ] x.T = [a0 a1 a2 b0 b1 b2 c3]
- 参数:
- src(N, 2) 类似数组
源坐标。
- dst(N, 2) 类似数组
目标坐标。
- weights(N,) 类似数组, 可选
每对点的相对权重值。
- 返回:
- successbool
如果模型估计成功,则为 True。
- 属性 inverse#
返回一个表示逆变换的变换对象。
- class skimage.transform.SimilarityTransform(matrix=None, scale=None, rotation=None, translation=None, *, dimensionality=2)[source]#
-
相似变换。
在 2D 中具有以下形式
X = a0 * x - b0 * y + a1 = = s * x * cos(rotation) - s * y * sin(rotation) + a1 Y = b0 * x + a0 * y + b1 = = s * x * sin(rotation) + s * y * cos(rotation) + b1
其中
s是一个缩放因子,齐次变换矩阵是[[a0 -b0 a1] [b0 a0 b1] [0 0 1 ]]
相似变换通过一个额外的缩放因子扩展了欧几里得变换,此外还包括旋转和平移参数。
- 参数:
- matrix(dim+1, dim+1) 类数组,可选
齐次变换矩阵。
- scale浮点数,可选
缩放因子。仅针对 2D 和 3D 实现。
- rotationfloat,可选
旋转角度,顺时针方向,以弧度为单位。仅针对 2D 和 3D 实现。对于 3D,以 ZYX 欧拉角给出。
- translation(dim,) 类数组,可选
x, y[, z] 平移参数。仅针对 2D 和 3D 实现。
- 属性:
- params(dim+1, dim+1) 数组
齐次变换矩阵。
- 属性 dimensionality#
变换的维度。
- estimate(src, dst)[source]#
从一组对应的点估计变换。
您可以使用总最小二乘法确定过度、良好和欠定的参数。
源坐标和目标坐标的数量必须匹配。
- 参数:
- src(N, 2) 类似数组
源坐标。
- dst(N, 2) 类似数组
目标坐标。
- 返回:
- successbool
如果模型估计成功,则为 True。
- 属性 inverse#
返回一个表示逆变换的变换对象。
- residuals(src, dst)[source]#
确定变换后的目标坐标的残差。
对于每个变换后的源坐标,确定其到相应目标坐标的欧几里得距离。
- 参数:
- src(N, 2) 数组
源坐标。
- dst(N, 2) 数组
目标坐标。
- 返回:
- residuals(N,) 数组
坐标的残差。
- 属性 rotation#
- 属性 scale#
- 属性 translation#
- class skimage.transform.ThinPlateSplineTransform[source]#
基类:
object薄板样条变换。
给定两组匹配的点(源和目标),此类估计薄板样条 (TPS) 变换,该变换将源中的每个点变换为其目标对应点。
- 属性:
- src(N, 2) 类似数组
源图像中控制点的坐标。
参考文献
[1]Bookstein, Fred L. “主形变:薄板样条和形变的分解”,IEEE Transactions on pattern analysis and machine intelligence 11.6 (1989): 567–585. DOI:
10.1109/34.24792https://user.engineering.uiowa.edu/~aip/papers/bookstein-89.pdf示例
>>> import skimage as ski
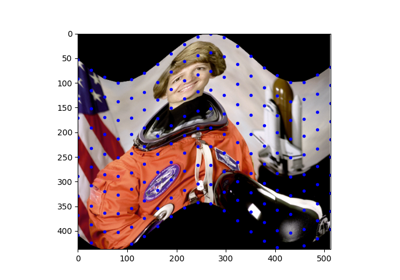
定义源和目标控制点,使其模拟旋转 90 度,并从中生成网格
>>> src = np.array([[0, 0], [0, 5], [5, 5], [5, 0]]) >>> dst = np.array([[5, 0], [0, 0], [0, 5], [5, 5]])
估计变换
>>> tps = ski.transform.ThinPlateSplineTransform() >>> tps.estimate(src, dst) True
将变换应用于
src接近于dst>>> np.round(tps(src)) array([[5., 0.], [0., 0.], [0., 5.], [5., 5.]])
创建一个网格以应用变换
>>> grid = np.meshgrid(np.arange(5), np.arange(5)) >>> grid[1] array([[0, 0, 0, 0, 0], [1, 1, 1, 1, 1], [2, 2, 2, 2, 2], [3, 3, 3, 3, 3], [4, 4, 4, 4, 4]])
>>> coords = np.vstack([grid[0].ravel(), grid[1].ravel()]).T >>> transformed = tps(coords) >>> np.round(transformed[:, 1]).reshape(5, 5).astype(int) array([[0, 1, 2, 3, 4], [0, 1, 2, 3, 4], [0, 1, 2, 3, 4], [0, 1, 2, 3, 4], [0, 1, 2, 3, 4]])
- estimate(src, dst)[源代码]#
估计源点和目标点之间的最佳样条映射。
- 参数:
- src(N, 2) 类似数组
源坐标处的控制点。
- dst(N, 2) 类似数组
目标坐标处的控制点。
- 返回:
- success: bool
True 表示估计成功。
注释
源点和目标点的数量 N 必须匹配。
- property inverse#