注意

转到结尾下载完整的示例代码。或通过 Binder 在浏览器中运行此示例

拉东变换#

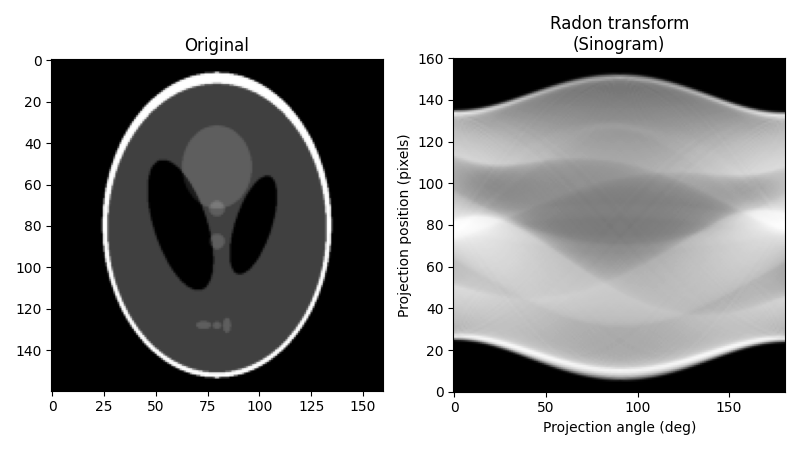
在计算机断层扫描中，断层扫描重建问题是从一组投影中获取断层扫描切片图像 [1]。投影是通过在 2D 感兴趣的对象中绘制一组平行射线形成的，将对象对比度沿每条射线的积分分配给投影中的单个像素。2D 对象的单个投影是一维的。为了实现对象的计算机断层扫描重建，必须获取几个投影，每个投影对应于射线相对于对象的不同角度。几个角度的投影集合称为正弦图，它是原始图像的线性变换。

反拉东变换用于计算机断层扫描，以从测量的投影（正弦图）重建 2D 图像。反拉东变换的实际、精确实现不存在，但有几种可用的良好近似算法。

由于反拉东变换从一组投影重建对象，因此（正向）拉东变换可用于模拟断层扫描实验。

此脚本执行拉东变换以模拟断层扫描实验，并根据模拟形成的正弦图重建输入图像。比较了两种执行反拉东变换和重建原始图像的方法：滤波反投影 (FBP) 和同步代数重建技术 (SART)。

有关断层扫描重建的更多信息，请参阅

正向变换#

作为我们的原始图像，我们将使用 Shepp-Logan 幻影。在计算拉东变换时，我们需要决定要使用多少投影角度。根据经验，投影的数量应与对象中的像素数大致相同（要了解为什么会这样，请考虑在重建过程中必须确定多少个未知像素值，并将其与投影提供的测量次数进行比较），我们在此遵循该规则。下面是原始图像及其拉东变换，通常称为其正弦图

import numpy as np
import matplotlib.pyplot as plt

from skimage.data import shepp_logan_phantom
from skimage.transform import radon, rescale

image = shepp_logan_phantom()
image = rescale(image, scale=0.4, mode='reflect', channel_axis=None)

fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(8, 4.5))

ax1.set_title("Original")
ax1.imshow(image, cmap=plt.cm.Greys_r)

theta = np.linspace(0.0, 180.0, max(image.shape), endpoint=False)
sinogram = radon(image, theta=theta)
dx, dy = 0.5 * 180.0 / max(image.shape), 0.5 / sinogram.shape[0]
ax2.set_title("Radon transform\n(Sinogram)")
ax2.set_xlabel("Projection angle (deg)")
ax2.set_ylabel("Projection position (pixels)")
ax2.imshow(
    sinogram,
    cmap=plt.cm.Greys_r,
    extent=(-dx, 180.0 + dx, -dy, sinogram.shape[0] + dy),
    aspect='auto',
)

fig.tight_layout()
plt.show()
Original, Radon transform (Sinogram)

使用滤波反投影 (FBP) 进行重建#

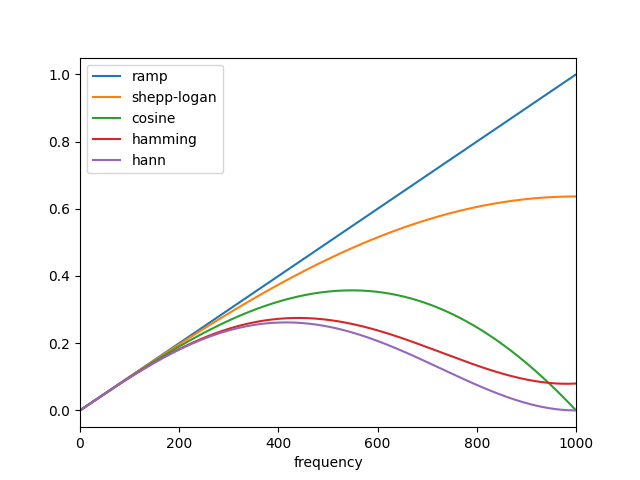
滤波反投影的数学基础是傅里叶切片定理 [2]。它使用投影的傅里叶变换和傅里叶空间中的插值来获得图像的 2D 傅里叶变换，然后将其反转以形成重建图像。滤波反投影是执行反拉东变换的最快方法之一。FBP 的唯一可调参数是滤波器，该滤波器应用于傅里叶变换的投影。它可用于抑制重建中的高频噪声。skimage 提供了 ‘ramp’、‘shepp-logan’、‘cosine’、‘hamming’ 和 ‘hann’ 滤波器

import matplotlib.pyplot as plt
from skimage.transform.radon_transform import _get_fourier_filter

filters = ['ramp', 'shepp-logan', 'cosine', 'hamming', 'hann']

for ix, f in enumerate(filters):
    response = _get_fourier_filter(2000, f)
    plt.plot(response, label=f)

plt.xlim([0, 1000])
plt.xlabel('frequency')
plt.legend()
plt.show()
plot radon transform

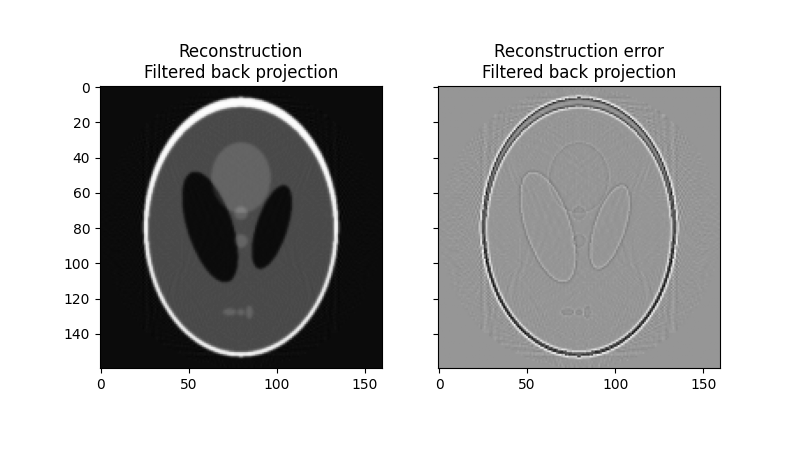
使用 ‘ramp’ 滤波器应用反拉东变换，我们得到

from skimage.transform import iradon

reconstruction_fbp = iradon(sinogram, theta=theta, filter_name='ramp')
error = reconstruction_fbp - image
print(f'FBP rms reconstruction error: {np.sqrt(np.mean(error**2)):.3g}')

imkwargs = dict(vmin=-0.2, vmax=0.2)
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(8, 4.5), sharex=True, sharey=True)
ax1.set_title("Reconstruction\nFiltered back projection")
ax1.imshow(reconstruction_fbp, cmap=plt.cm.Greys_r)
ax2.set_title("Reconstruction error\nFiltered back projection")
ax2.imshow(reconstruction_fbp - image, cmap=plt.cm.Greys_r, **imkwargs)
plt.show()
Reconstruction Filtered back projection, Reconstruction error Filtered back projection
FBP rms reconstruction error: 0.0283

使用同步代数重建技术进行重建#

断层扫描的代数重建技术基于一个直接的思想：对于像素化图像，特定投影中单个射线的值只是射线在穿过对象时穿过的所有像素的总和。这是表达正向拉东变换的一种方式。然后，反拉东变换可以表示为一组（大的）线性方程。由于每条射线都穿过图像中一小部分的像素，因此这组方程是稀疏的，从而允许稀疏线性系统的迭代求解器来处理方程组。一种迭代方法特别受欢迎，即 Kaczmarz 方法 [3]，它具有这样的特性：解将接近方程组的最小二乘解。

将重建问题表示为一组线性方程和迭代求解器的组合使代数技术相对灵活，因此可以相对轻松地纳入某些形式的先验知识。

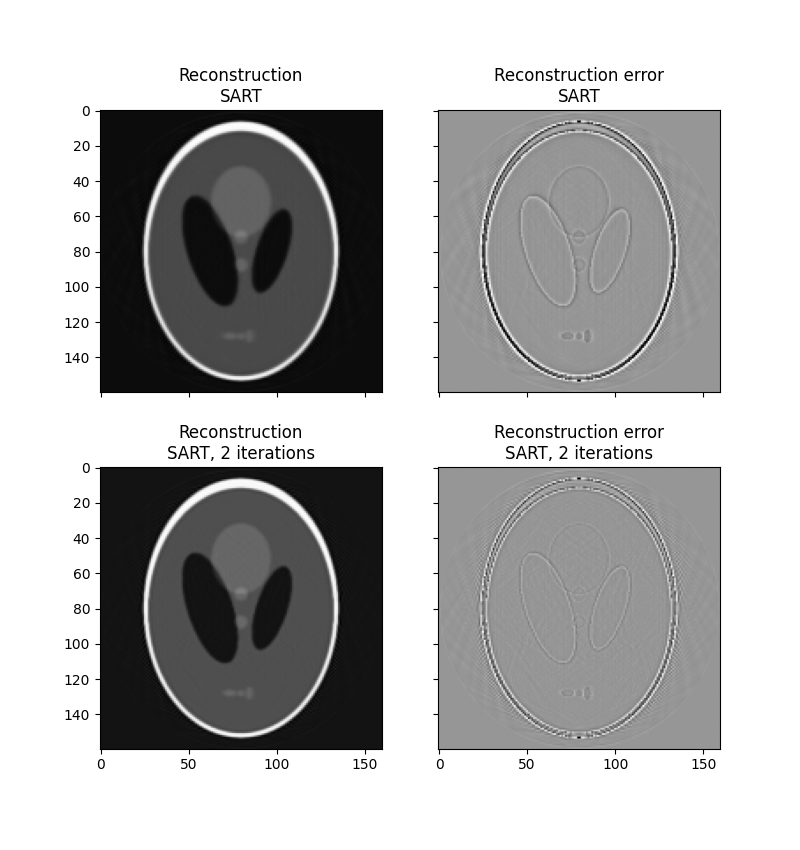
skimage 提供了代数重建技术的一种更流行的变体：同步代数重建技术 (SART) [4]。它使用 Kaczmarz 的方法作为迭代求解器。通常在一次迭代中获得良好的重建，从而使该方法在计算上有效。运行一个或多个额外的迭代通常会改善尖锐的高频特征的重建，并减少均方误差，但会增加高频噪声（用户需要决定哪种迭代次数最适合手头的问题）。skimage 中的实现允许将重建值的下限和上限形式的先验信息提供给重建。

from skimage.transform import iradon_sart

reconstruction_sart = iradon_sart(sinogram, theta=theta)
error = reconstruction_sart - image
print(
    f'SART (1 iteration) rms reconstruction error: ' f'{np.sqrt(np.mean(error**2)):.3g}'
)

fig, axes = plt.subplots(2, 2, figsize=(8, 8.5), sharex=True, sharey=True)
ax = axes.ravel()

ax[0].set_title("Reconstruction\nSART")
ax[0].imshow(reconstruction_sart, cmap=plt.cm.Greys_r)

ax[1].set_title("Reconstruction error\nSART")
ax[1].imshow(reconstruction_sart - image, cmap=plt.cm.Greys_r, **imkwargs)

# Run a second iteration of SART by supplying the reconstruction
# from the first iteration as an initial estimate
reconstruction_sart2 = iradon_sart(sinogram, theta=theta, image=reconstruction_sart)
error = reconstruction_sart2 - image
print(
    f'SART (2 iterations) rms reconstruction error: '
    f'{np.sqrt(np.mean(error**2)):.3g}'
)

ax[2].set_title("Reconstruction\nSART, 2 iterations")
ax[2].imshow(reconstruction_sart2, cmap=plt.cm.Greys_r)

ax[3].set_title("Reconstruction error\nSART, 2 iterations")
ax[3].imshow(reconstruction_sart2 - image, cmap=plt.cm.Greys_r, **imkwargs)
plt.show()
Reconstruction SART, Reconstruction error SART, Reconstruction SART, 2 iterations, Reconstruction error SART, 2 iterations
SART (1 iteration) rms reconstruction error: 0.0329
SART (2 iterations) rms reconstruction error: 0.0214

脚本总运行时间：（0 分钟 2.276 秒）

由 Sphinx-Gallery 生成的图库