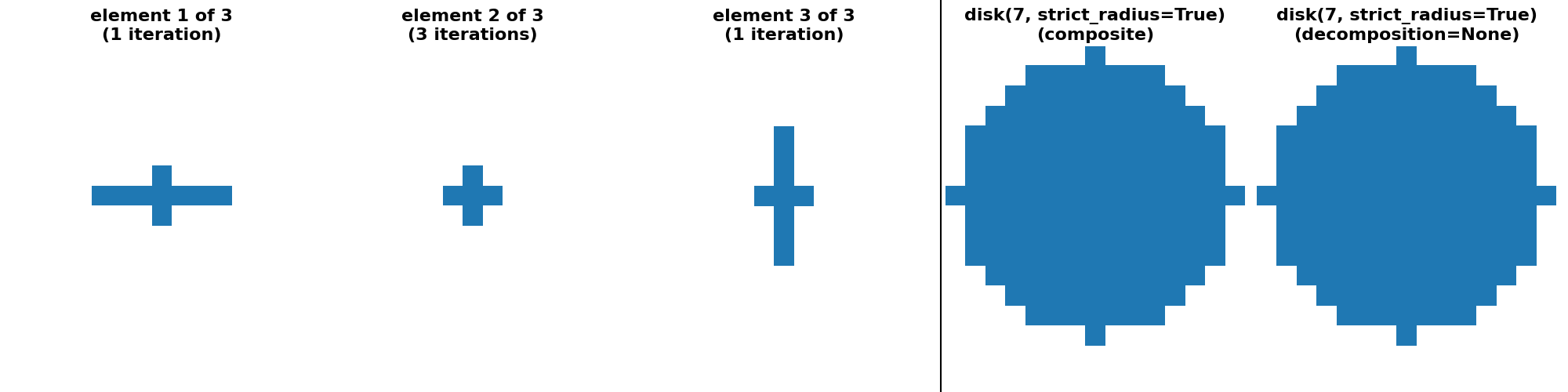注意
转到末尾下载完整的示例代码。或者通过 Binder 在浏览器中运行此示例
分解平面足迹(结构元素)#
许多足迹(结构元素)可以分解为一系列等效的较小结构元素。“平面”一词指的是仅包含 0 或 1 值的足迹(即,skimage.morphology.footprints 中的所有方法)。二值膨胀操作具有关联性和分配性,这通常允许分解为一系列等效的较小足迹。大多数情况下,这样做是为了提供性能优势。
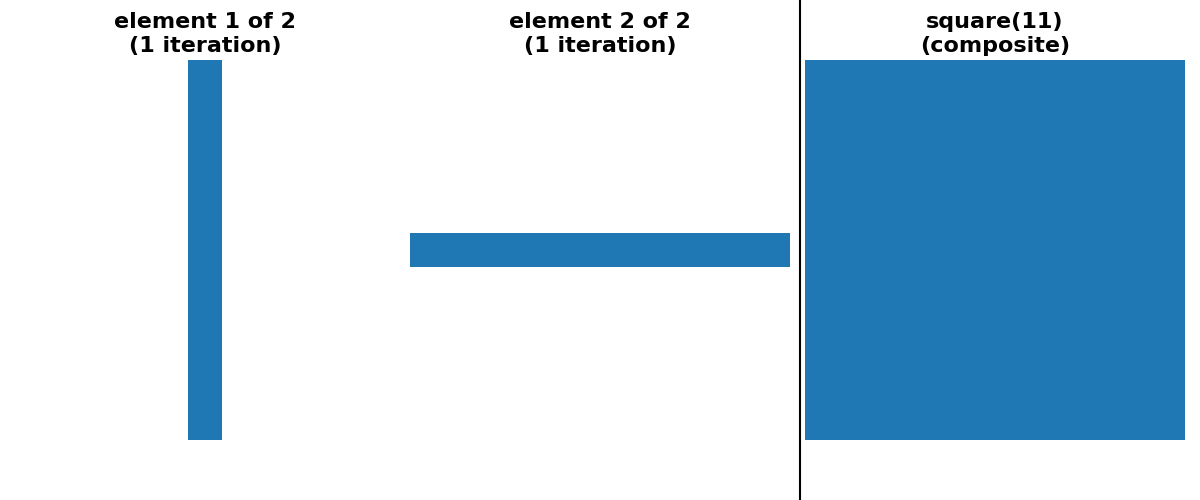
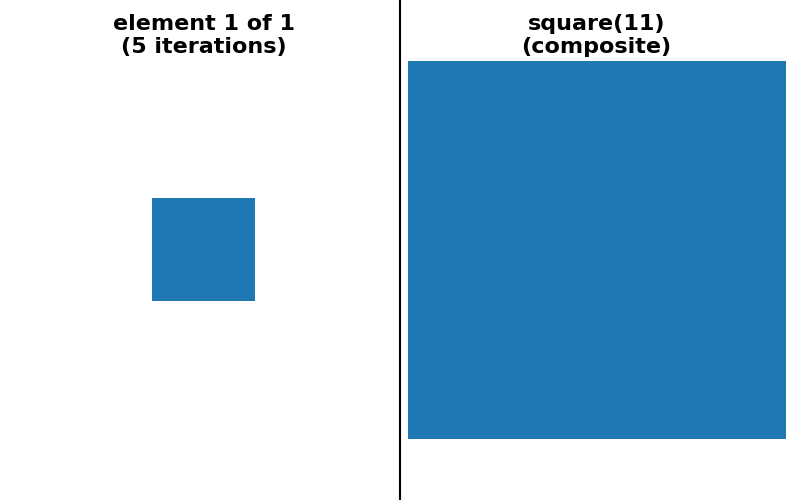
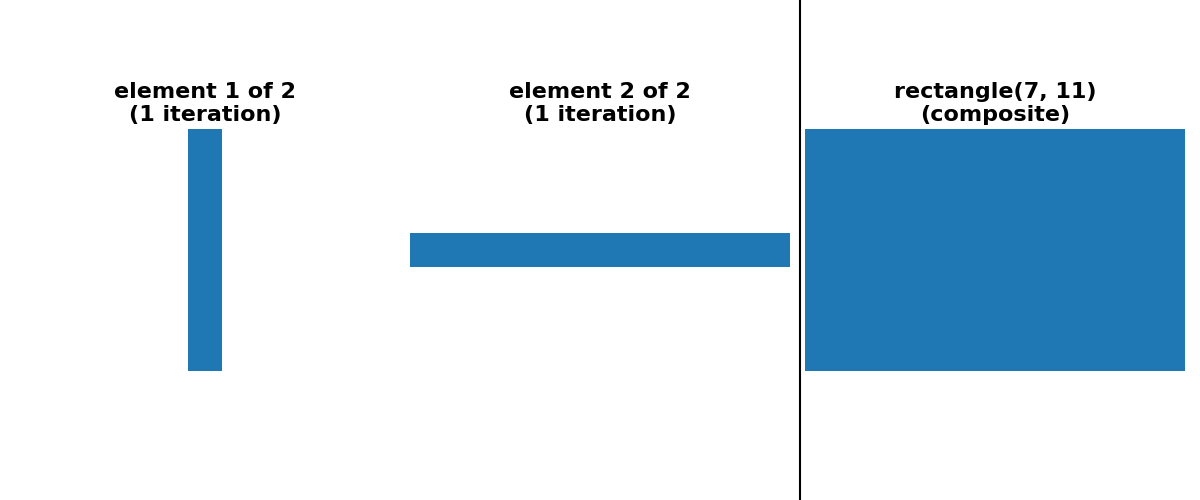
举一个具体的例子,使用形状为 (15, 15) 的方形足迹进行膨胀等效于使用形状为 (15, 1) 的矩形进行膨胀,然后使用形状为 (1, 15) 的矩形进行另一次膨胀。它也等效于使用形状为 (3, 3) 的方形足迹进行 7 次连续膨胀。
有许多可能的分解,哪种分解效果最好可能取决于架构。
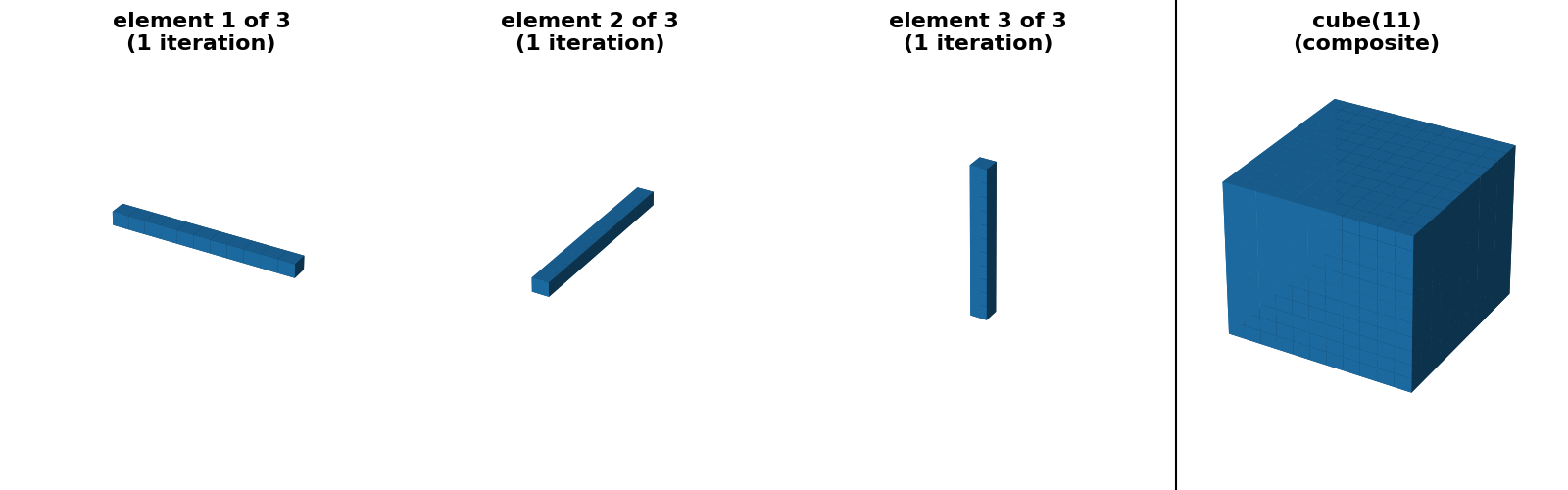
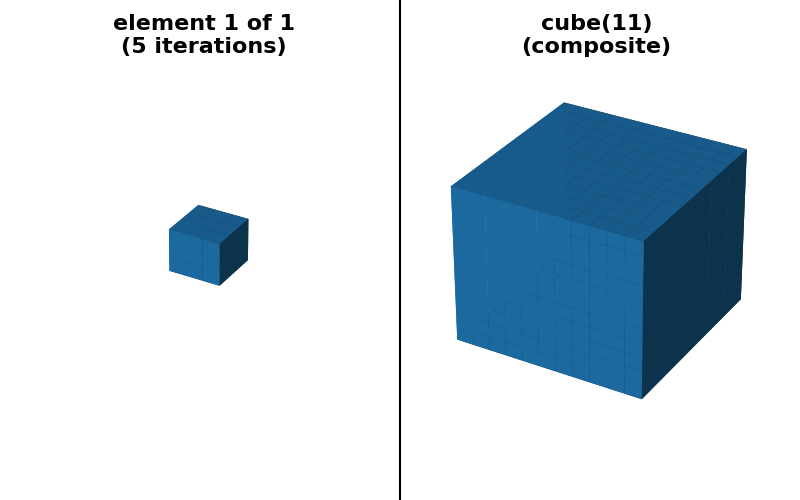
scikit-image 目前提供两种形式的自动分解。对于 square、rectangle 和 cube 足迹的情况,可以选择“可分离”分解(大小 > 1,一次只沿一个轴)。
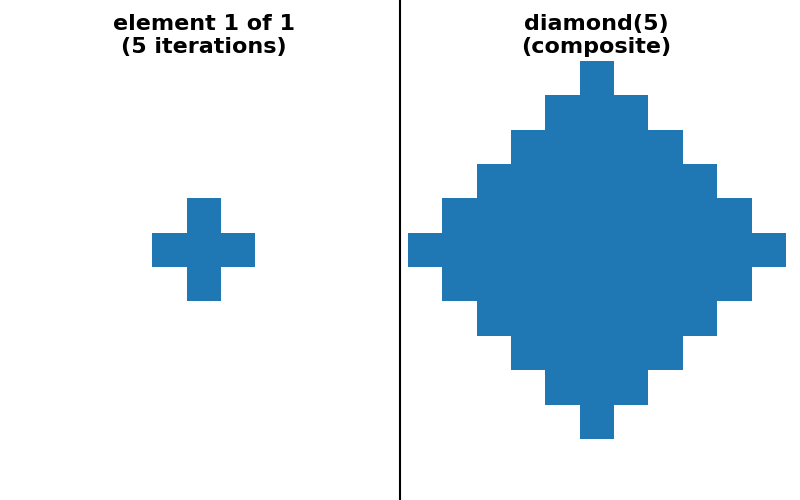
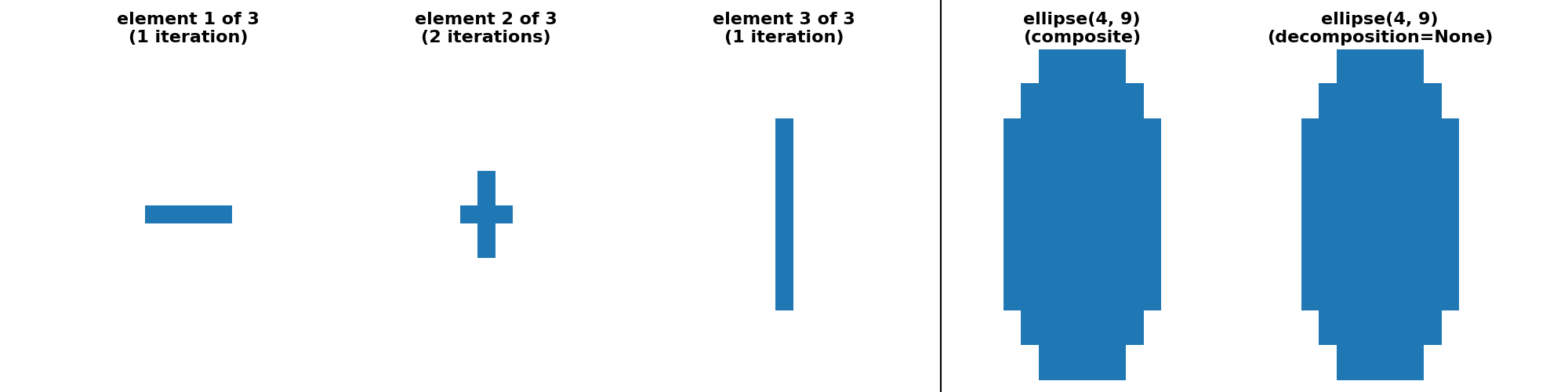
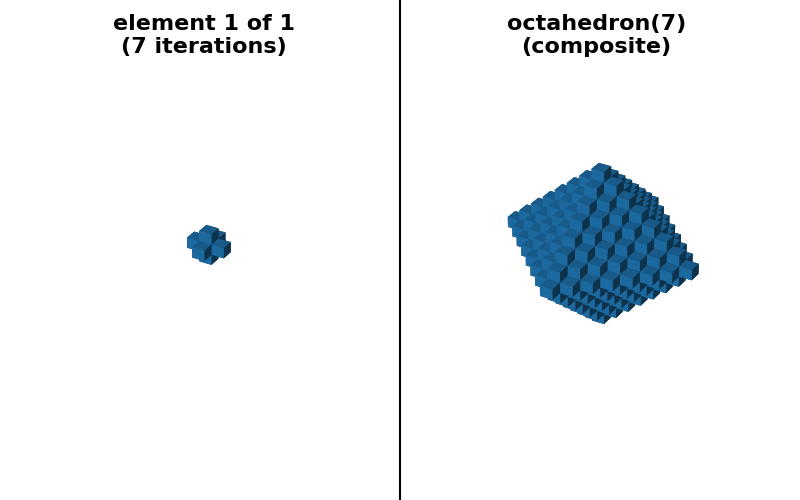
对于其他一些对称凸形状,例如 diamond、octahedron 和 octagon,没有分解成一维运算的可分离分解。但是,可以基于一系列形状为 (3,) * ndim 的小足迹来提供“序列”分解。
为了简化实现,下面显示的所有分解都仅使用奇数大小的足迹,其原点位于足迹的中心。
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import colors
from mpl_toolkits.mplot3d import Axes3D
from skimage.morphology import (
ball,
diamond,
disk,
ellipse,
octagon,
octahedron,
footprint_rectangle,
)
from skimage.morphology.footprints import footprint_from_sequence
# Generate 2D and 3D structuring elements.
footprint_dict = {
"square 11x11 (separable)": (
footprint_rectangle((11, 11), decomposition=None),
footprint_rectangle((11, 11), decomposition="separable"),
),
"square 11x11 (sequence)": (
footprint_rectangle((11, 11), decomposition=None),
footprint_rectangle((11, 11), decomposition="sequence"),
),
"rectangle 7x11 (separable)": (
footprint_rectangle((7, 11), decomposition=None),
footprint_rectangle((7, 11), decomposition="separable"),
),
"rectangle 7x11 (sequence)": (
footprint_rectangle((7, 11), decomposition=None),
footprint_rectangle((7, 11), decomposition="sequence"),
),
"diamond(5) (sequence)": (
diamond(5, decomposition=None),
diamond(5, decomposition="sequence"),
),
"disk(7, strict_radius=False) (sequence)": (
disk(7, strict_radius=False, decomposition=None),
disk(7, strict_radius=False, decomposition="sequence"),
),
"disk(7, strict_radius=True) (crosses)": (
disk(7, strict_radius=True, decomposition=None),
disk(7, strict_radius=True, decomposition="crosses"),
),
"ellipse(4, 9) (crosses)": (
ellipse(4, 9, decomposition=None),
ellipse(4, 9, decomposition="crosses"),
),
"disk(20) (sequence)": (
disk(20, strict_radius=False, decomposition=None),
disk(20, strict_radius=False, decomposition="sequence"),
),
"octagon(7, 4) (sequence)": (
octagon(7, 4, decomposition=None),
octagon(7, 4, decomposition="sequence"),
),
"cube 11x11x11 (separable)": (
footprint_rectangle((11, 11, 11), decomposition=None),
footprint_rectangle((11, 11, 11), decomposition="separable"),
),
"cube 11x11x11 (sequence)": (
footprint_rectangle((11, 11, 11), decomposition=None),
footprint_rectangle((11, 11, 11), decomposition="sequence"),
),
"octahedron(7) (sequence)": (
octahedron(7, decomposition=None),
octahedron(7, decomposition="sequence"),
),
"ball(9) (sequence)": (
ball(9, strict_radius=False, decomposition=None),
ball(9, strict_radius=False, decomposition="sequence"),
),
}
# Visualize the elements
# binary white / blue colormap
cmap = colors.ListedColormap(['white', (0.1216, 0.4706, 0.70588)])
fontdict = dict(fontsize=16, fontweight='bold')
for title, (footprint, footprint_sequence) in footprint_dict.items():
ndim = footprint.ndim
num_seq = len(footprint_sequence)
approximate_decomposition = 'ball' in title or 'disk' in title or 'ellipse' in title
if approximate_decomposition:
# Two extra plot in approximate cases to show both:
# 1.) decomposition=None idea footprint
# 2.) actual composite footprint corresponding to the sequence
num_subplots = num_seq + 2
else:
# composite and decomposition=None are identical so only 1 extra plot
num_subplots = num_seq + 1
fig = plt.figure(figsize=(4 * num_subplots, 5))
if ndim == 2:
ax = fig.add_subplot(1, num_subplots, num_subplots)
ax.imshow(footprint, cmap=cmap, vmin=0, vmax=1)
if approximate_decomposition:
ax2 = fig.add_subplot(1, num_subplots, num_subplots - 1)
footprint_composite = footprint_from_sequence(footprint_sequence)
ax2.imshow(footprint_composite, cmap=cmap, vmin=0, vmax=1)
else:
ax = fig.add_subplot(1, num_subplots, num_subplots, projection=Axes3D.name)
ax.voxels(footprint, cmap=cmap)
if approximate_decomposition:
ax2 = fig.add_subplot(
1, num_subplots, num_subplots - 1, projection=Axes3D.name
)
footprint_composite = footprint_from_sequence(footprint_sequence)
ax2.voxels(footprint_composite, cmap=cmap)
title1 = title.split(' (')[0]
if approximate_decomposition:
# plot decomposition=None on a separate axis from the composite
title = title1 + '\n(decomposition=None)'
else:
# for exact cases composite and decomposition=None are identical
title = title1 + '\n(composite)'
ax.set_title(title, fontdict=fontdict)
ax.set_axis_off()
if approximate_decomposition:
ax2.set_title(title1 + '\n(composite)', fontdict=fontdict)
ax2.set_axis_off()
for n, (fp, num_reps) in enumerate(footprint_sequence):
npad = [((footprint.shape[d] - fp.shape[d]) // 2,) * 2 for d in range(ndim)]
fp = np.pad(fp, npad, mode='constant')
if ndim == 2:
ax = fig.add_subplot(1, num_subplots, n + 1)
ax.imshow(fp, cmap=cmap, vmin=0, vmax=1)
else:
ax = fig.add_subplot(1, num_subplots, n + 1, projection=Axes3D.name)
ax.voxels(fp, cmap=cmap)
title = f"element {n + 1} of {num_seq}\n({num_reps} iteration"
title += "s)" if num_reps > 1 else ")"
ax.set_title(title, fontdict=fontdict)
ax.set_axis_off()
ax.set_xlabel(f'num_reps = {num_reps}')
fig.tight_layout()
# draw a line separating the sequence elements from the composite
line_pos = num_seq / num_subplots
line = plt.Line2D([line_pos, line_pos], [0, 1], color="black")
fig.add_artist(line)
plt.show()
脚本的总运行时间: (0 分钟 11.348 秒)