在图像中使用窗口函数

快速傅里叶变换 (FFT) 假设被变换的数据表示周期信号的一个周期。 因此，在 FFT 的上下文中，要变换的信号的端点可能会表现为不连续性。 这些不连续性会扭曲 FFT 的输出，导致来自“真实”频率分量的能量泄漏到更广泛的频率中。

可以通过将信号与窗口函数相乘来减少频谱泄漏的影响。 窗口化会在信号到达边缘时平滑地降低其幅度，从而消除了由 FFT 引起的人为不连续性的影响。

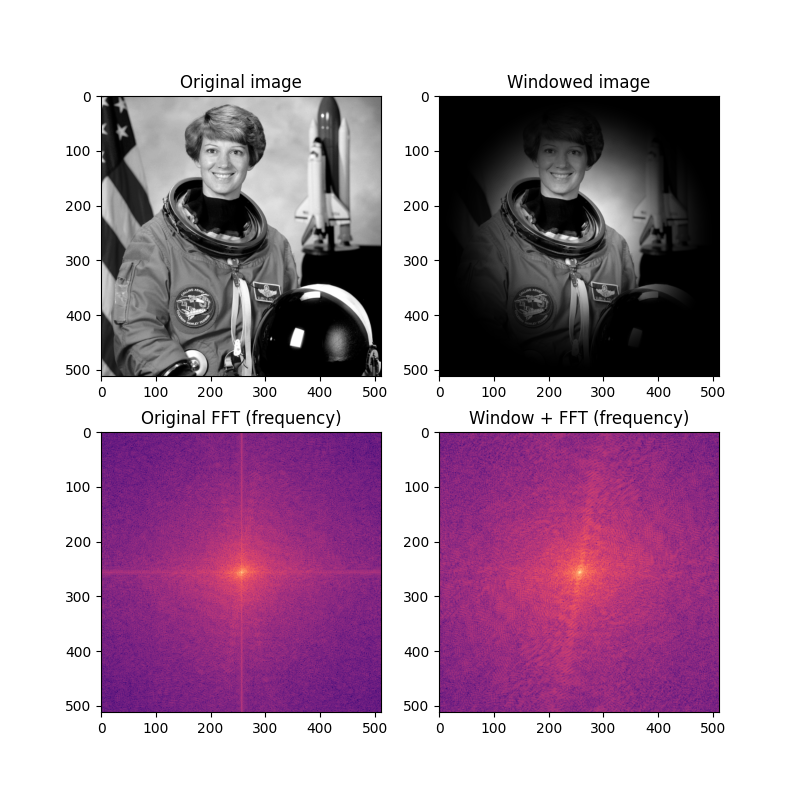
在此示例中，我们看到典型图像的 FFT 可以显示沿 x 和 y 轴的强烈频谱泄漏（请参见图中的垂直和水平线）。 应用二维汉恩窗口大大减少了频谱泄漏，使“真实”频率信息在 FFT 的频率分量图中更加可见。

import matplotlib.pyplot as plt
import numpy as np
from scipy.fft import fft2, fftshift
from skimage import img_as_float
from skimage.color import rgb2gray
from skimage.data import astronaut
from skimage.filters import window

image = img_as_float(rgb2gray(astronaut()))

wimage = image * window('hann', image.shape)

image_f = np.abs(fftshift(fft2(image)))
wimage_f = np.abs(fftshift(fft2(wimage)))

fig, axes = plt.subplots(2, 2, figsize=(8, 8))
ax = axes.ravel()
ax[0].set_title("Original image")
ax[0].imshow(image, cmap='gray')
ax[1].set_title("Windowed image")
ax[1].imshow(wimage, cmap='gray')
ax[2].set_title("Original FFT (frequency)")
ax[2].imshow(np.log(image_f), cmap='magma')
ax[3].set_title("Window + FFT (frequency)")
ax[3].imshow(np.log(wimage_f), cmap='magma')
plt.show()