熵

在信息论中，信息熵是消息可能结果数的对数以 2 为底。

对于图像，局部熵与给定邻域中包含的复杂度相关，通常由结构元素定义。熵滤波器可以检测局部灰度级分布的细微变化。

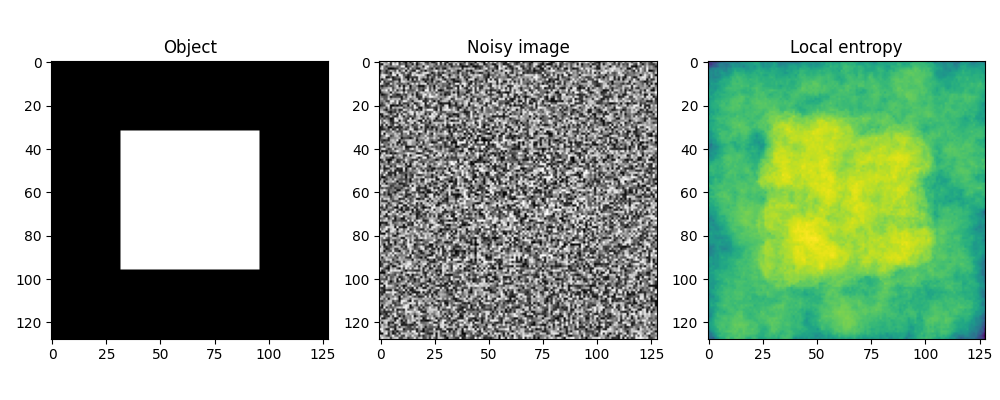
在第一个示例中，图像由两个表面组成，这两个表面具有两个略微不同的分布。图像在图像中间的范围 [-15，+15] 内具有均匀随机分布，在图像边界的范围 [-14，14] 内具有均匀随机分布，两者都以 128 的灰度值为中心。为了检测中心正方形，我们使用足够大的半径的圆形结构元素计算局部熵度量，以捕获局部灰度级分布。第二个示例展示了如何使用较小的结构元素检测相机图像中的纹理。

对象检测

import matplotlib.pyplot as plt
import numpy as np

from skimage import data
from skimage.util import img_as_ubyte
from skimage.filters.rank import entropy
from skimage.morphology import disk

rng = np.random.default_rng()

noise_mask = np.full((128, 128), 28, dtype=np.uint8)
noise_mask[32:-32, 32:-32] = 30

noise = (noise_mask * rng.random(noise_mask.shape) - 0.5 * noise_mask).astype(np.uint8)
img = noise + 128

entr_img = entropy(img, disk(10))

fig, (ax0, ax1, ax2) = plt.subplots(nrows=1, ncols=3, figsize=(10, 4))

img0 = ax0.imshow(noise_mask, cmap='gray')
ax0.set_title("Object")
ax1.imshow(img, cmap='gray')
ax1.set_title("Noisy image")
ax2.imshow(entr_img, cmap='viridis')
ax2.set_title("Local entropy")

fig.tight_layout()

纹理检测

image = img_as_ubyte(data.camera())

fig, (ax0, ax1) = plt.subplots(ncols=2, figsize=(12, 4), sharex=True, sharey=True)

img0 = ax0.imshow(image, cmap=plt.cm.gray)
ax0.set_title("Image")
ax0.axis("off")
fig.colorbar(img0, ax=ax0)

img1 = ax1.imshow(entropy(image, disk(5)), cmap='gray')
ax1.set_title("Entropy")
ax1.axis("off")
fig.colorbar(img1, ax=ax1)

fig.tight_layout()

plt.show()