估计模糊强度

此示例显示了 measure.blur_effect 中实现的度量如何表现，既作为模糊强度的函数，也作为重新模糊滤波器大小的函数。这种无参考感知模糊度量在[1]中描述。

[1]

Frederique Crete, Thierry Dolmiere, Patricia Ladret, 和 Marina Nicolas “模糊效应：使用新的无参考感知模糊度量进行感知和估计” Proc. SPIE 6492, 人类视觉和电子成像 XII, 64920I (2007) https://hal.archives-ouvertes.fr/hal-00232709 DOI:10.1117/12.702790

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import scipy.ndimage as ndi

import plotly
import plotly.express as px
from skimage import color, data, measure

生成一系列逐渐模糊的图像

让我们加载一个通过 scikit-image 的数据注册表可用的图像。模糊度量适用于单通道图像。

image = data.astronaut()
image = color.rgb2gray(image)

让我们使用一系列大小递增的均匀滤波器来模糊此图像。

blurred_images = [ndi.uniform_filter(image, size=k) for k in range(2, 32, 2)]
img_stack = np.stack(blurred_images)

fig = px.imshow(
    img_stack,
    animation_frame=0,
    binary_string=True,
    labels={'animation_frame': 'blur strength ~'},
)
plotly.io.show(fig)

绘制模糊度量

让我们计算所有模糊图像的模糊度量：我们期望它随着模糊强度的增加而向 1 增加。我们计算了三个不同值的重新模糊滤波器：3、11（默认）和 30。

B = pd.DataFrame(
    data=np.zeros((len(blurred_images), 3)),
    columns=['h_size = 3', 'h_size = 11', 'h_size = 30'],
)
for ind, im in enumerate(blurred_images):
    B.loc[ind, 'h_size = 3'] = measure.blur_effect(im, h_size=3)
    B.loc[ind, 'h_size = 11'] = measure.blur_effect(im, h_size=11)
    B.loc[ind, 'h_size = 30'] = measure.blur_effect(im, h_size=30)

B.plot().set(
    xlabel='blur strength (half the size of uniform filter)', ylabel='blur metric'
)

plt.show()

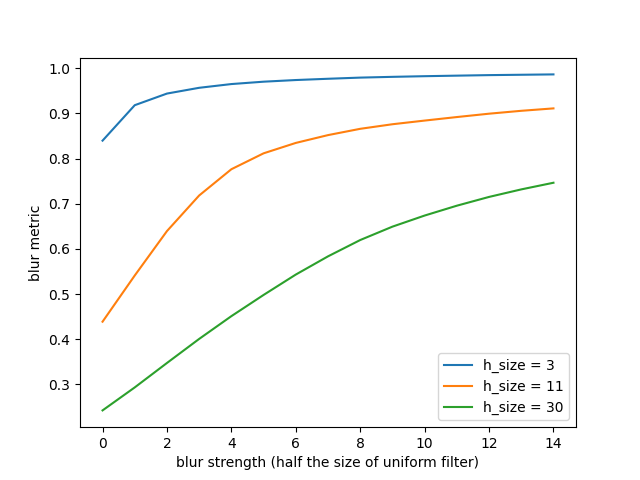
我们可以看到，一旦模糊强度大于（达到与）均匀滤波器的大小，该度量就会接近 1，因此，随着模糊强度的增加，它会渐近趋于 1。11 像素的值给出的模糊度量与人类感知最相关。这就是它成为感知模糊度量 measure.blur_effect 实现中的默认值的原因。