形态学滤波

形态学图像处理是与图像中特征的形状或形态相关的非线性操作的集合，例如边界、骨架等。 在任何给定的技术中，我们使用称为结构元素的小形状或模板来探测图像，该结构元素定义像素周围的感兴趣区域或邻域。

本文档概述以下基本形态学操作

1. 腐蚀

2. 膨胀

3. 开运算

4. 闭运算

5. 白色顶帽

6. 黑色顶帽

7. 骨架化

8. 凸包

首先，让我们使用 io.imread 加载图像。 请注意，形态学函数仅适用于灰度或二进制图像，因此我们设置 as_gray=True。

import matplotlib.pyplot as plt
from skimage import data
from skimage.util import img_as_ubyte

orig_phantom = img_as_ubyte(data.shepp_logan_phantom())
fig, ax = plt.subplots()
ax.imshow(orig_phantom, cmap=plt.cm.gray)

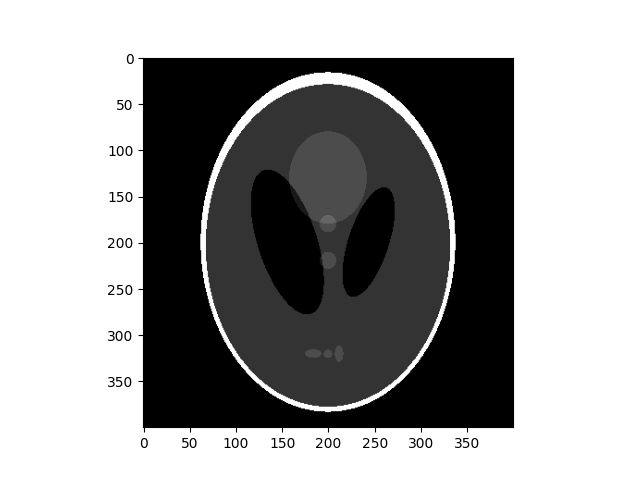
<matplotlib.image.AxesImage object at 0x7f036a3059a0>

我们还定义一个用于绘制比较的便利函数

def plot_comparison(original, filtered, filter_name):
    fig, (ax1, ax2) = plt.subplots(ncols=2, figsize=(8, 4), sharex=True, sharey=True)
    ax1.imshow(original, cmap=plt.cm.gray)
    ax1.set_title('original')
    ax1.set_axis_off()
    ax2.imshow(filtered, cmap=plt.cm.gray)
    ax2.set_title(filter_name)
    ax2.set_axis_off()

腐蚀

形态学 腐蚀 将 (i, j) 处的像素设置为以 (i, j) 为中心的邻域中所有像素的最小值。 传递给 腐蚀 的结构元素 footprint 是一个布尔数组，描述了该邻域。 下面，我们使用 disk 创建一个圆形结构元素，我们将其用于以下大多数示例。

from skimage.morphology import erosion, dilation, opening, closing, white_tophat
from skimage.morphology import black_tophat, skeletonize, convex_hull_image
from skimage.morphology import disk

footprint = disk(6)
eroded = erosion(orig_phantom, footprint)
plot_comparison(orig_phantom, eroded, 'erosion')

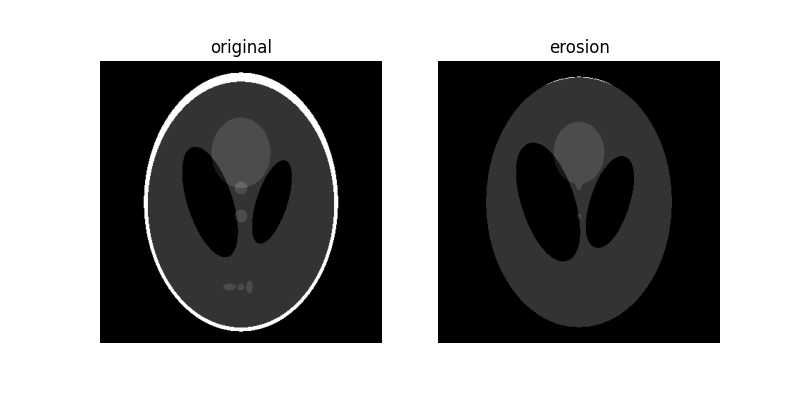
请注意，随着我们增加磁盘的大小，图像的白色边界如何消失或被腐蚀。 另请注意中心处的两个黑色椭圆的尺寸增加以及图像下部 3 个浅灰色斑块的消失。

膨胀

形态学 膨胀 将 (i, j) 处的像素设置为以 (i, j) 为中心的邻域中所有像素的最大值。 膨胀会扩大明亮区域并缩小黑暗区域。

dilated = dilation(orig_phantom, footprint)
plot_comparison(orig_phantom, dilated, 'dilation')

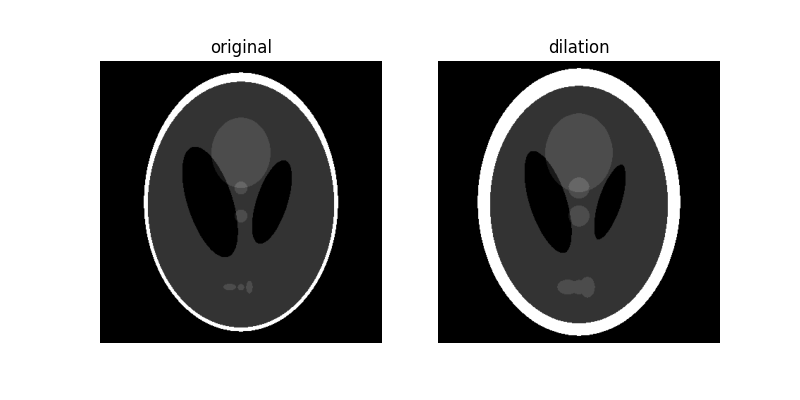
请注意，随着我们增加磁盘的大小，图像的白色边界如何加厚或被膨胀。 另请注意中心处两个黑色椭圆的尺寸减小，以及中心处的浅灰色圆圈和图像下部的 3 个斑块的加厚。

开运算

图像上的形态学 开运算 定义为先腐蚀后膨胀。 开运算可以去除小的亮点（即“盐”）并连接小的黑暗裂缝。

opened = opening(orig_phantom, footprint)
plot_comparison(orig_phantom, opened, 'opening')

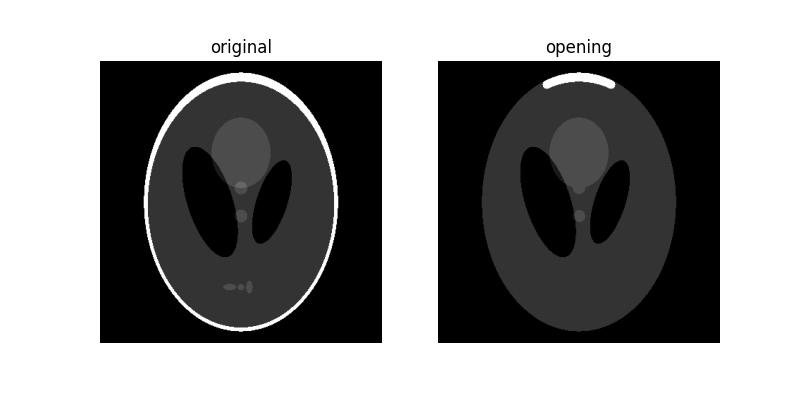
由于 开运算 图像以腐蚀操作开始，因此会删除小于结构元素的明亮区域。 随后的膨胀操作确保大于结构元素的明亮区域保留其原始大小。 请注意，中心处的亮暗形状如何保留其原始厚度，但底部的 3 个较亮的斑块被完全腐蚀。 外白色环突出了大小依赖性：比结构元素薄的环的部分被完全擦除，而顶部的较厚区域保留其原始厚度。

闭运算

图像上的形态学 闭运算 定义为先膨胀后腐蚀。 闭运算可以去除小的暗点（即“胡椒”）并连接小的明亮裂缝。

为了更清楚地说明这一点，让我们在白色边框上添加一个小的裂缝

phantom = orig_phantom.copy()
phantom[10:30, 200:210] = 0

closed = closing(phantom, footprint)
plot_comparison(phantom, closed, 'closing')

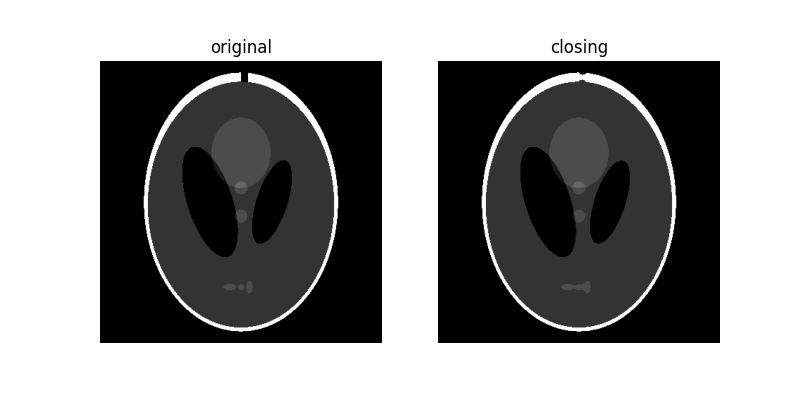
由于 闭运算 图像以膨胀操作开始，因此会删除小于结构元素的黑暗区域。 随后的腐蚀操作确保大于结构元素的黑暗区域保留其原始大小。 请注意底部的白色椭圆如何因膨胀而连接，但其他黑暗区域保留其原始大小。 另请注意，我们添加的裂缝大部分被去除。

白色顶帽

图像的white_tophat被定义为图像减去其形态学开运算的结果。此操作会返回图像中比结构元素小的亮斑。

为了增加趣味性，我们将在图像中添加亮斑和暗斑

phantom = orig_phantom.copy()
phantom[340:350, 200:210] = 255
phantom[100:110, 200:210] = 0

w_tophat = white_tophat(phantom, footprint)
plot_comparison(phantom, w_tophat, 'white tophat')

正如您所看到的，10 像素宽的白色正方形被突出显示，因为它比结构元素小。此外，大多数椭圆周围的细白色边缘也被保留下来，因为它们比结构元素小，但顶部的较厚区域消失了。

黑顶帽

图像的 black_tophat 定义为它的形态学闭运算减去原始图像。此操作返回图像中比结构元素小的暗斑。

b_tophat = black_tophat(phantom, footprint)
plot_comparison(phantom, b_tophat, 'black tophat')

正如您所看到的，10 像素宽的黑色正方形被突出显示，因为它比结构元素小。

对偶性

您应该已经注意到，许多这些操作只是另一个操作的反向操作。这种对偶性可以总结如下

1. 腐蚀 <-> 膨胀

2. 开运算 <-> 闭运算

3. 白顶帽 <-> 黑顶帽

骨架化

细化用于将二值图像中的每个连通分量减少到单像素宽的骨架。重要的是要注意，这仅在二值图像上执行。

horse = data.horse()

sk = skeletonize(horse == 0)
plot_comparison(horse, sk, 'skeletonize')

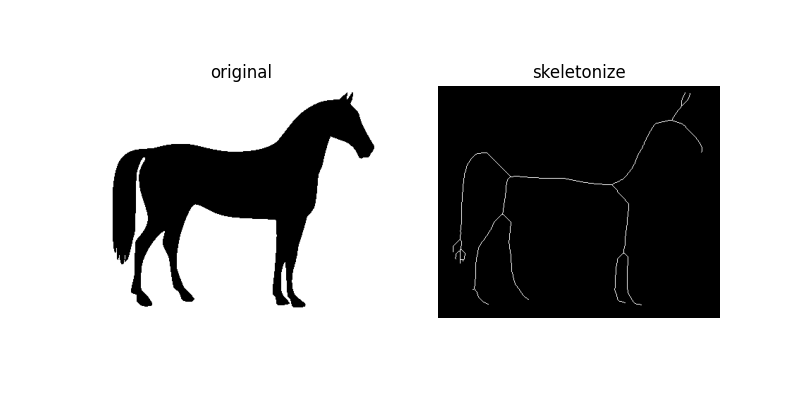
顾名思义，此技术通过连续应用细化来将图像细化为 1 像素宽的骨架。

凸包

convex_hull_image 是包含在围绕输入图像中所有白色像素的最小凸多边形中的像素集。再次注意，这也是在二值图像上执行的。

hull1 = convex_hull_image(horse == 0)
plot_comparison(horse, hull1, 'convex hull')

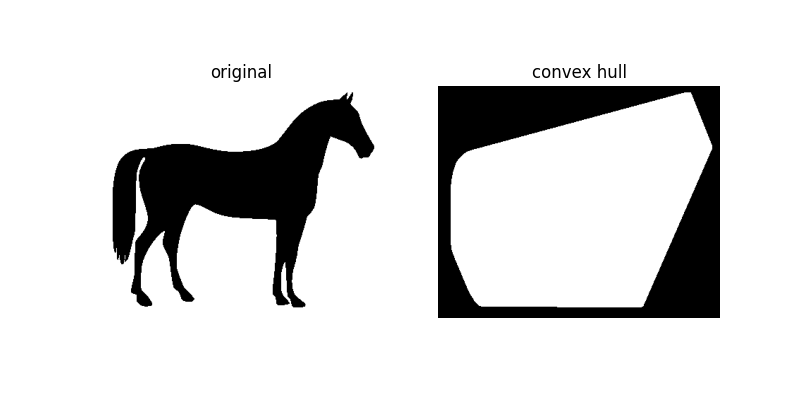
如图所示，convex_hull_image 给出了完全覆盖图像中白色或 True 的最小多边形。

如果我们在图像中添加一个小颗粒，我们可以看到凸包如何适应以包围该颗粒

horse_mask = horse == 0
horse_mask[45:50, 75:80] = 1

hull2 = convex_hull_image(horse_mask)
plot_comparison(horse_mask, hull2, 'convex hull')

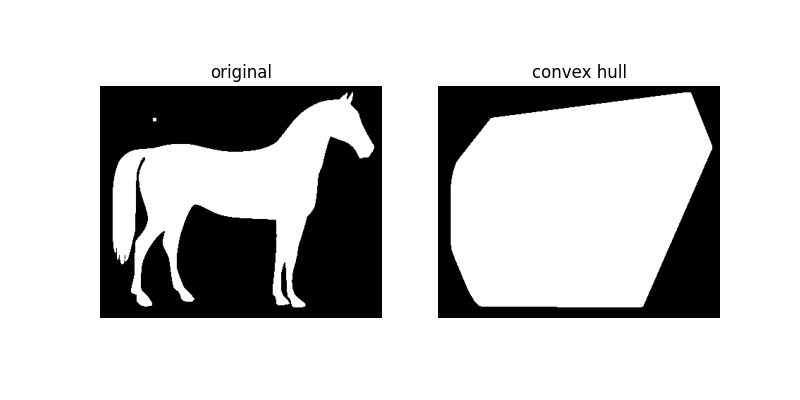
其他资源

1. MathWorks 关于形态学处理的教程

2. 奥克兰大学关于形态学图像处理的教程

3. https://en.wikipedia.org/wiki/Mathematical_morphology

plt.show()