圆形和椭圆形霍夫变换

霍夫变换在其最简单的形式中是一种 检测直线的方法，但它也可以用于检测圆形或椭圆形。该算法假设边缘已检测到，并且对噪声或缺失点具有鲁棒性。

圆形检测

在以下示例中，霍夫变换用于检测硬币位置并匹配其边缘。我们提供了一系列合理的半径。对于每个半径，提取两个圆，最后保留五个最突出的候选圆。结果表明硬币位置得到了很好的检测。

算法概述

给定白色背景上的黑色圆圈，我们首先猜测其半径（或一系列半径）以构建一个新圆圈。此圆圈应用于原始图片的每个黑色像素，并且此圆圈的坐标在累加器中进行投票。根据这种几何构造，原始圆圈中心位置获得最高分数。

请注意，累加器的大小被构建为大于原始图片，以便检测框架外的中心。其大小扩展了两倍于较大半径。

import numpy as np
import matplotlib.pyplot as plt

from skimage import data, color
from skimage.transform import hough_circle, hough_circle_peaks
from skimage.feature import canny
from skimage.draw import circle_perimeter
from skimage.util import img_as_ubyte


# Load picture and detect edges
image = img_as_ubyte(data.coins()[160:230, 70:270])
edges = canny(image, sigma=3, low_threshold=10, high_threshold=50)


# Detect two radii
hough_radii = np.arange(20, 35, 2)
hough_res = hough_circle(edges, hough_radii)

# Select the most prominent 3 circles
accums, cx, cy, radii = hough_circle_peaks(hough_res, hough_radii, total_num_peaks=3)

# Draw them
fig, ax = plt.subplots(ncols=1, nrows=1, figsize=(10, 4))
image = color.gray2rgb(image)
for center_y, center_x, radius in zip(cy, cx, radii):
    circy, circx = circle_perimeter(center_y, center_x, radius, shape=image.shape)
    image[circy, circx] = (220, 20, 20)

ax.imshow(image, cmap=plt.cm.gray)
plt.show()

椭圆检测

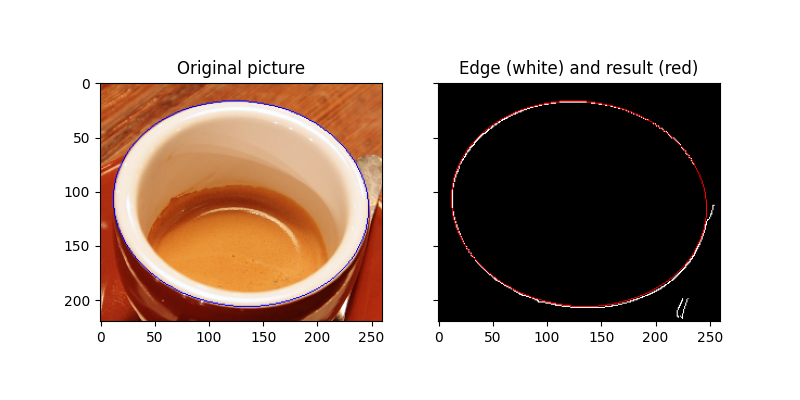
在此第二个示例中，目标是检测咖啡杯的边缘。基本上，这是圆形的投影，即椭圆。要解决的问题要困难得多，因为必须确定五个参数，而不是圆形的三个参数。

算法概述

该算法获取属于椭圆的两个不同的点。它假设这两个点形成长轴。对所有其他点的循环确定候选椭圆的短轴长度。如果足够多的“有效”候选对象具有相似的短轴长度，则后者将包含在结果中。有效是指短轴和长轴长度在规定的范围内。可以在参考文献 [1] 中找到算法的完整描述。

参考文献

[1]

Xie, Yonghong 和 Qiang Ji。“一种新的高效椭圆检测方法。”模式识别，2002 年。第 16 届国际会议论文集。第 2 卷。IEEE，2002 年

import matplotlib.pyplot as plt

from skimage import data, color, img_as_ubyte
from skimage.feature import canny
from skimage.transform import hough_ellipse
from skimage.draw import ellipse_perimeter

# Load picture, convert to grayscale and detect edges
image_rgb = data.coffee()[0:220, 160:420]
image_gray = color.rgb2gray(image_rgb)
edges = canny(image_gray, sigma=2.0, low_threshold=0.55, high_threshold=0.8)

# Perform a Hough Transform
# The accuracy corresponds to the bin size of the histogram for minor axis lengths.
# A higher `accuracy` value will lead to more ellipses being found, at the
# cost of a lower precision on the minor axis length estimation.
# A higher `threshold` will lead to less ellipses being found, filtering out those
# with fewer edge points (as found above by the Canny detector) on their perimeter.
result = hough_ellipse(edges, accuracy=20, threshold=250, min_size=100, max_size=120)
result.sort(order='accumulator')

# Estimated parameters for the ellipse
best = list(result[-1])
yc, xc, a, b = (int(round(x)) for x in best[1:5])
orientation = best[5]

# Draw the ellipse on the original image
cy, cx = ellipse_perimeter(yc, xc, a, b, orientation)
image_rgb[cy, cx] = (0, 0, 255)
# Draw the edge (white) and the resulting ellipse (red)
edges = color.gray2rgb(img_as_ubyte(edges))
edges[cy, cx] = (250, 0, 0)

fig2, (ax1, ax2) = plt.subplots(
    ncols=2, nrows=1, figsize=(8, 4), sharex=True, sharey=True
)

ax1.set_title('Original picture')
ax1.imshow(image_rgb)

ax2.set_title('Edge (white) and result (red)')
ax2.imshow(edges)

plt.show()