注意
转到结尾下载完整示例代码。 或通过 Binder 在浏览器中运行此示例
Max-tree#
max-tree 是图像的层次结构表示,是大量形态学滤波器的基础。
如果我们将阈值操作应用于图像,我们会获得包含一个或多个连接组件的二值图像。 如果我们应用较低的阈值,则来自较高阈值的所有连接组件都包含在来自较低阈值的连接组件中。 这自然地定义了一个嵌套组件的层次结构,可以用树来表示。 每当通过阈值 t1 获得的连接组件 A 包含在通过阈值 t1 < t2 获得的组件 B 中时,我们说 B 是 A 的父级。 生成的树结构称为组件树。 max-tree 是这种组件树的紧凑表示。 [1], [2], [3], [4]
在这个例子中,我们给出了一个关于 max-tree 是什么的直观理解。
参考文献#
在我们开始之前:一些辅助函数
def plot_img(ax, image, title, plot_text, image_values):
"""Plot an image, overlaying image values or indices."""
ax.imshow(image, cmap='gray', aspect='equal', vmin=0, vmax=np.max(image))
ax.set_title(title)
ax.set_yticks([])
ax.set_xticks([])
for x in np.arange(-0.5, image.shape[0], 1.0):
ax.add_artist(
Line2D((x, x), (-0.5, image.shape[0] - 0.5), color='blue', linewidth=2)
)
for y in np.arange(-0.5, image.shape[1], 1.0):
ax.add_artist(Line2D((-0.5, image.shape[1]), (y, y), color='blue', linewidth=2))
if plot_text:
for i, j in np.ndindex(*image_values.shape):
ax.text(
j,
i,
image_values[i, j],
fontsize=8,
horizontalalignment='center',
verticalalignment='center',
color='red',
)
return
def prune(G, node, res):
"""Transform a canonical max tree to a max tree."""
value = G.nodes[node]['value']
res[node] = str(node)
preds = [p for p in G.predecessors(node)]
for p in preds:
if G.nodes[p]['value'] == value:
res[node] += f", {p}"
G.remove_node(p)
else:
prune(G, p, res)
G.nodes[node]['label'] = res[node]
return
def accumulate(G, node, res):
"""Transform a max tree to a component tree."""
total = G.nodes[node]['label']
parents = G.predecessors(node)
for p in parents:
total += ', ' + accumulate(G, p, res)
res[node] = total
return total
def position_nodes_for_max_tree(G, image_rav, root_x=4, delta_x=1.2):
"""Set the position of nodes of a max-tree.
This function helps to visually distinguish between nodes at the same
level of the hierarchy and nodes at different levels.
"""
pos = {}
for node in reversed(list(nx.topological_sort(canonical_max_tree))):
value = G.nodes[node]['value']
if canonical_max_tree.out_degree(node) == 0:
# root
pos[node] = (root_x, value)
in_nodes = [y for y in canonical_max_tree.predecessors(node)]
# place the nodes at the same level
level_nodes = [y for y in filter(lambda x: image_rav[x] == value, in_nodes)]
nb_level_nodes = len(level_nodes) + 1
c = nb_level_nodes // 2
i = -c
if len(level_nodes) < 3:
hy = 0
m = 0
else:
hy = 0.25
m = hy / (c - 1)
for level_node in level_nodes:
if i == 0:
i += 1
if len(level_nodes) < 3:
pos[level_node] = (pos[node][0] + i * 0.6 * delta_x, value)
else:
pos[level_node] = (
pos[node][0] + i * 0.6 * delta_x,
value + m * (2 * np.abs(i) - c - 1),
)
i += 1
# place the nodes at different levels
other_level_nodes = [
y for y in filter(lambda x: image_rav[x] > value, in_nodes)
]
if len(other_level_nodes) == 1:
i = 0
else:
i = -len(other_level_nodes) // 2
for other_level_node in other_level_nodes:
if (len(other_level_nodes) % 2 == 0) and (i == 0):
i += 1
pos[other_level_node] = (
pos[node][0] + i * delta_x,
image_rav[other_level_node],
)
i += 1
return pos
def plot_tree(graph, positions, ax, *, title='', labels=None, font_size=8, text_size=8):
"""Plot max and component trees."""
nx.draw_networkx(
graph,
pos=positions,
ax=ax,
node_size=40,
node_shape='s',
node_color='white',
font_size=font_size,
labels=labels,
)
for v in range(image_rav.min(), image_rav.max() + 1):
ax.hlines(v - 0.5, -3, 10, linestyles='dotted')
ax.text(-3, v - 0.15, f"val: {v}", fontsize=text_size)
ax.hlines(v + 0.5, -3, 10, linestyles='dotted')
ax.set_xlim(-3, 10)
ax.set_title(title)
ax.set_axis_off()
图像定义#
我们定义一个小的测试图像。 为了清楚起见,我们选择一个示例图像,其中图像值不能与索引混淆(不同的范围)。
Max-tree#
接下来,我们计算此图像的 max-tree。 图像的 max-tree
图像绘图#
然后,我们可视化图像及其展开的索引。 具体来说,我们绘制带有以下覆盖层的图像: - 图像值 - 展开的索引(用作像素标识符) - max_tree 函数的输出
# raveled image
image_rav = image.ravel()
# raveled indices of the example image (for display purpose)
raveled_indices = np.arange(image.size).reshape(image.shape)
fig, (ax1, ax2, ax3) = plt.subplots(1, 3, sharey=True, figsize=(9, 3))
plot_img(ax1, image - image.min(), 'Image Values', plot_text=True, image_values=image)
plot_img(
ax2,
image - image.min(),
'Raveled Indices',
plot_text=True,
image_values=raveled_indices,
)
plot_img(ax3, image - image.min(), 'Max-tree indices', plot_text=True, image_values=P)
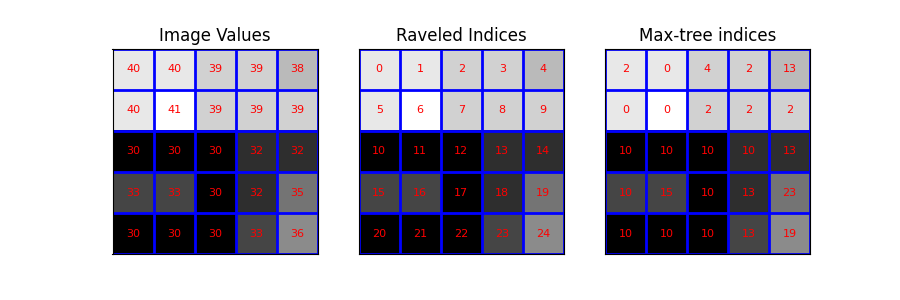
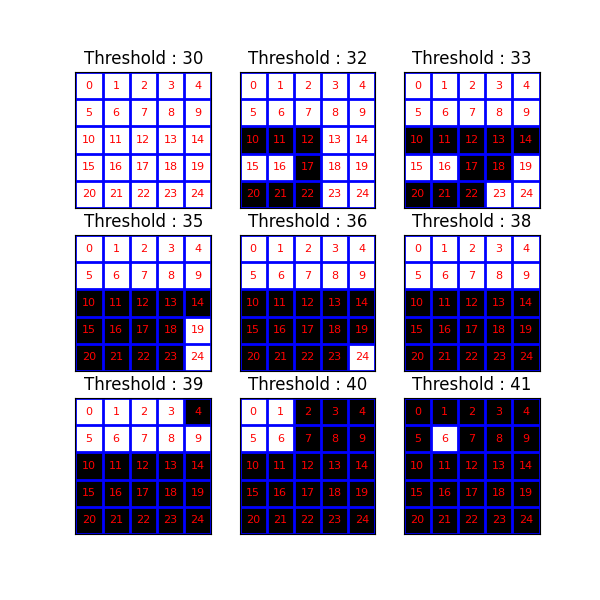
可视化阈值操作#
现在,我们研究一系列阈值操作的结果。 组件树(和 max-tree)提供了不同级别连接组件之间包含关系的表示。
fig, axes = plt.subplots(3, 3, sharey=True, sharex=True, figsize=(6, 6))
thresholds = np.unique(image)
for k, threshold in enumerate(thresholds):
bin_img = image >= threshold
plot_img(
axes[(k // 3), (k % 3)],
bin_img,
f"Threshold : {threshold}",
plot_text=True,
image_values=raveled_indices,
)
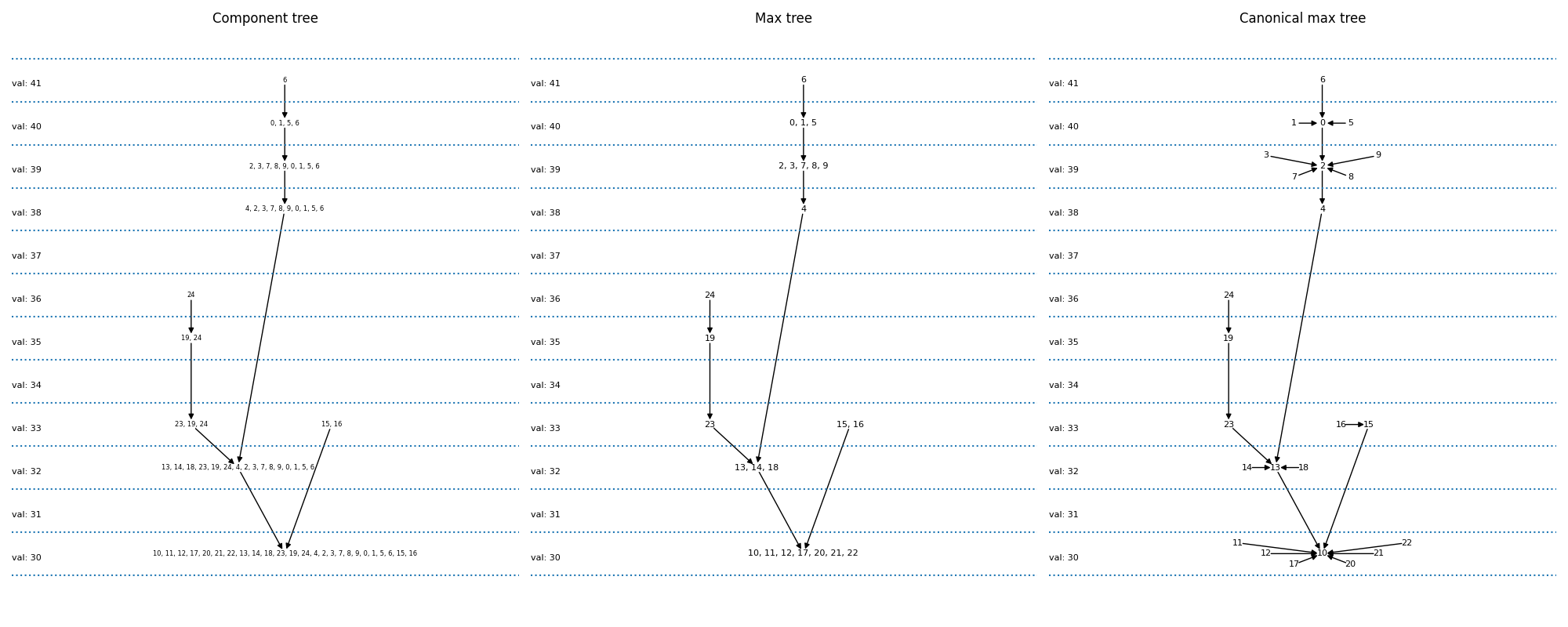
Max-tree 绘图#
现在,我们绘制组件树和 max-tree。 组件树将所有可能的阈值操作产生的不同像素集相互关联。 如果一个级别的组件包含在较低级别的组件中,则图中会有一个箭头。 max-tree 只是像素集的不同编码。
组件树:像素集被明确地写出来。 例如,我们看到 {6}(在 41 处应用阈值的结果)是 {0, 1, 5, 6}(在 40 处应用阈值)的父级。
max-tree:只有在此级别进入集合的像素被明确地写出来。 因此,我们将写入 {6} -> {0,1,5} 而不是 {6} -> {0, 1, 5, 6}
规范 max-treeL 这是我们的实现给出的表示。 在这里,每个像素都是一个节点。 多个像素的连接组件由其中一个像素表示。 因此,我们将 {6} -> {0,1,5} 替换为 {6} -> {5}、{1} -> {5}、{0} -> {5} 这允许我们通过图像(顶行,第三列)表示图形。
# the canonical max-tree graph
canonical_max_tree = nx.DiGraph()
canonical_max_tree.add_nodes_from(S)
for node in canonical_max_tree.nodes():
canonical_max_tree.nodes[node]['value'] = image_rav[node]
canonical_max_tree.add_edges_from([(n, P_rav[n]) for n in S[1:]])
# max-tree from the canonical max-tree
nx_max_tree = nx.DiGraph(canonical_max_tree)
labels = {}
prune(nx_max_tree, S[0], labels)
# component tree from the max-tree
labels_ct = {}
total = accumulate(nx_max_tree, S[0], labels_ct)
# positions of nodes : canonical max-tree (CMT)
pos_cmt = position_nodes_for_max_tree(canonical_max_tree, image_rav)
# positions of nodes : max-tree (MT)
pos_mt = dict(zip(nx_max_tree.nodes, [pos_cmt[node] for node in nx_max_tree.nodes]))
# plot the trees with networkx and matplotlib
fig, (ax1, ax2, ax3) = plt.subplots(1, 3, sharey=True, figsize=(20, 8))
plot_tree(
nx_max_tree,
pos_mt,
ax1,
title='Component tree',
labels=labels_ct,
font_size=6,
text_size=8,
)
plot_tree(nx_max_tree, pos_mt, ax2, title='Max tree', labels=labels)
plot_tree(canonical_max_tree, pos_cmt, ax3, title='Canonical max tree')
fig.tight_layout()
plt.show()
脚本的总运行时间:(0 分钟 1.556 秒)
