使用 RANSAC 的鲁棒直线模型估计

在本示例中，我们将了解如何使用 RANSAC（随机样本一致性）算法对有缺陷的数据进行鲁棒地拟合直线模型。

首先，通过向线性函数添加高斯噪声来生成数据。然后，将异常点添加到数据集中。

RANSAC 迭代地从数据集中估计参数。在每次迭代中，将执行以下步骤

1. 从原始数据中选择 min_samples 个随机样本，并检查数据集是否有效（参见 is_data_valid 选项）。

2. 根据随机子集估计模型 (model_cls.estimate(*data[random_subset])，并检查估计的模型是否有效（参见 is_model_valid 选项）。

3. 通过使用估计的模型计算残差 (model_cls.residuals(*data)) 将所有数据点分类为内点或外点 - 所有残差小于 residual_threshold 的数据样本都被视为内点。

4. 如果内点样本的数量大于以往任何时候，则将估计的模型保存为最佳模型。如果当前估计的模型具有相同的内点数，则只有在残差之和小于的情况下才将其视为最佳模型。

这些步骤将执行最大次数，或直到满足某个特殊的停止条件。最终模型使用先前确定的最佳模型的所有内点样本进行估计。

import numpy as np
from matplotlib import pyplot as plt

from skimage.measure import LineModelND, ransac

rng = np.random.default_rng()

# generate coordinates of line
x = np.arange(-200, 200)
y = 0.2 * x + 20
data = np.column_stack([x, y])

# add gaussian noise to coordinates
noise = rng.normal(size=data.shape)
data += 0.5 * noise
data[::2] += 5 * noise[::2]
data[::4] += 20 * noise[::4]

# add faulty data
faulty = np.array(30 * [(180.0, -100)])
faulty += 10 * rng.normal(size=faulty.shape)
data[: faulty.shape[0]] = faulty

# fit line using all data
model = LineModelND()
model.estimate(data)

# robustly fit line only using inlier data with RANSAC algorithm
model_robust, inliers = ransac(
    data, LineModelND, min_samples=2, residual_threshold=1, max_trials=1000
)
outliers = inliers == False

# generate coordinates of estimated models
line_x = np.arange(-250, 250)
line_y = model.predict_y(line_x)
line_y_robust = model_robust.predict_y(line_x)

fig, ax = plt.subplots()
ax.plot(data[inliers, 0], data[inliers, 1], '.b', alpha=0.6, label='Inlier data')
ax.plot(data[outliers, 0], data[outliers, 1], '.r', alpha=0.6, label='Outlier data')
ax.plot(line_x, line_y, '-k', label='Line model from all data')
ax.plot(line_x, line_y_robust, '-b', label='Robust line model')
ax.legend(loc='lower left')
plt.show()

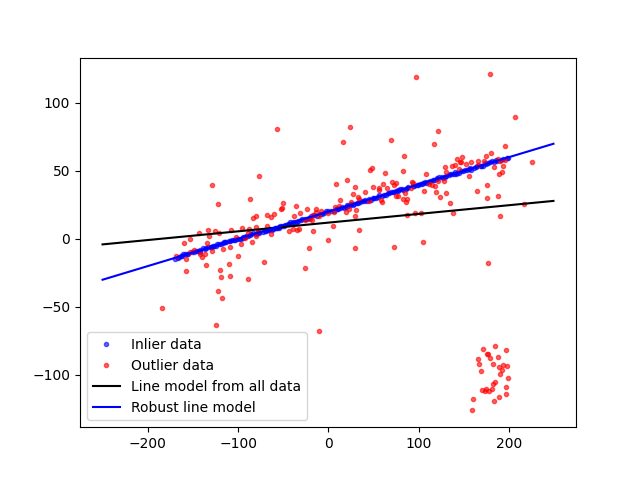
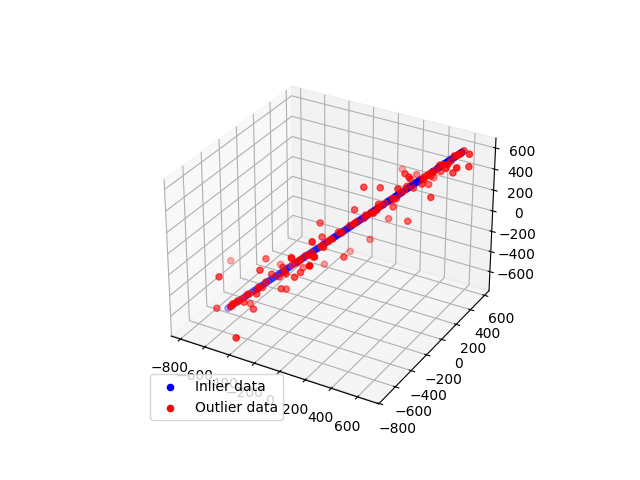
现在，我们将此示例推广到 3D 点。

import numpy as np
from matplotlib import pyplot as plt
from skimage.measure import LineModelND, ransac


# generate coordinates of line
point = np.array([0, 0, 0], dtype='float')
direction = np.array([1, 1, 1], dtype='float') / np.sqrt(3)
xyz = point + 10 * np.arange(-100, 100)[..., np.newaxis] * direction

# add gaussian noise to coordinates
noise = rng.normal(size=xyz.shape)
xyz += 0.5 * noise
xyz[::2] += 20 * noise[::2]
xyz[::4] += 100 * noise[::4]

# robustly fit line only using inlier data with RANSAC algorithm
model_robust, inliers = ransac(
    xyz, LineModelND, min_samples=2, residual_threshold=1, max_trials=1000
)
outliers = inliers == False

fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.scatter(
    xyz[inliers][:, 0],
    xyz[inliers][:, 1],
    xyz[inliers][:, 2],
    c='b',
    marker='o',
    label='Inlier data',
)
ax.scatter(
    xyz[outliers][:, 0],
    xyz[outliers][:, 1],
    xyz[outliers][:, 2],
    c='r',
    marker='o',
    label='Outlier data',
)
ax.legend(loc='lower left')
plt.show()