区域边界 RAG 的分层合并

此示例演示如何在区域边界区域邻接图 (RAG) 上执行分层合并。可以使用 skimage.graph.rag_boundary() 函数构造区域边界 RAG。具有最低边缘权重的区域会连续合并，直到没有权重小于 thresh 的边缘。分层合并通过 skimage.graph.merge_hierarchical() 函数完成。有关如何构造基于区域边界的 RAG 的示例，请参阅基于区域边界的区域邻接图 (RAG)。

• 
• 
• 

from skimage import data, segmentation, filters, color
from skimage import graph
from matplotlib import pyplot as plt


def weight_boundary(graph, src, dst, n):
    """
    Handle merging of nodes of a region boundary region adjacency graph.

    This function computes the `"weight"` and the count `"count"`
    attributes of the edge between `n` and the node formed after
    merging `src` and `dst`.


    Parameters
    ----------
    graph : RAG
        The graph under consideration.
    src, dst : int
        The vertices in `graph` to be merged.
    n : int
        A neighbor of `src` or `dst` or both.

    Returns
    -------
    data : dict
        A dictionary with the "weight" and "count" attributes to be
        assigned for the merged node.

    """
    default = {'weight': 0.0, 'count': 0}

    count_src = graph[src].get(n, default)['count']
    count_dst = graph[dst].get(n, default)['count']

    weight_src = graph[src].get(n, default)['weight']
    weight_dst = graph[dst].get(n, default)['weight']

    count = count_src + count_dst
    return {
        'count': count,
        'weight': (count_src * weight_src + count_dst * weight_dst) / count,
    }


def merge_boundary(graph, src, dst):
    """Call back called before merging 2 nodes.

    In this case we don't need to do any computation here.
    """
    pass


img = data.coffee()
edges = filters.sobel(color.rgb2gray(img))
labels = segmentation.slic(img, compactness=30, n_segments=400, start_label=1)
g = graph.rag_boundary(labels, edges)

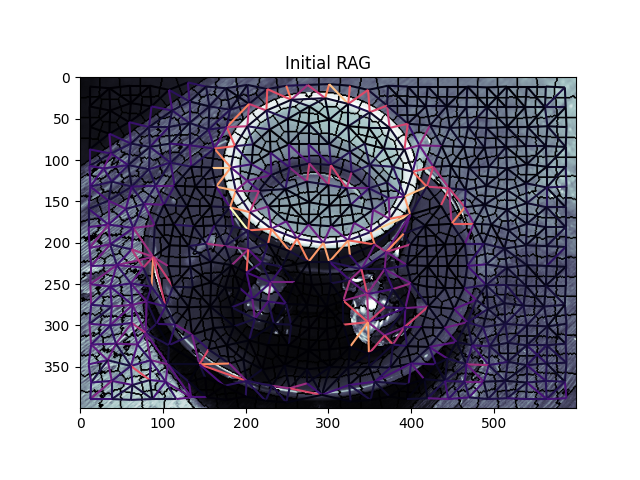
graph.show_rag(labels, g, img)
plt.title('Initial RAG')

labels2 = graph.merge_hierarchical(
    labels,
    g,
    thresh=0.08,
    rag_copy=False,
    in_place_merge=True,
    merge_func=merge_boundary,
    weight_func=weight_boundary,
)

graph.show_rag(labels, g, img)
plt.title('RAG after hierarchical merging')

plt.figure()
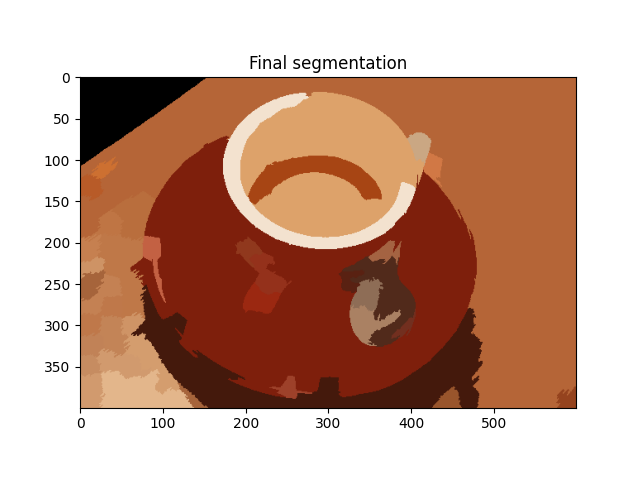
out = color.label2rgb(labels2, img, kind='avg', bg_label=0)
plt.imshow(out)
plt.title('Final segmentation')

plt.show()