`skimage.util`#

通用实用程序。

此模块包含许多用于处理一般图像的实用函数。

`apply_parallel`	在数组上并行映射函数。
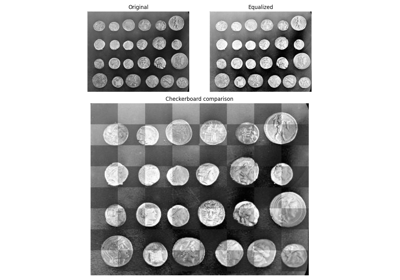
`compare_images`	返回显示两幅图像之间差异的图像。
`crop`	沿每个维度将数组 `ar` 裁剪 `crop_width`。
`dtype_limits`	返回图像的 dtype 的强度限制，即 (min, max) 元组。
`img_as_bool`	将图像转换为布尔格式。
`img_as_float`	将图像转换为浮点格式。
`img_as_float32`	将图像转换为单精度（32 位）浮点格式。
`img_as_float64`	将图像转换为双精度（64 位）浮点格式。
`img_as_int`	将图像转换为 16 位有符号整数格式。
`img_as_ubyte`	将图像转换为 8 位无符号整数格式。
`img_as_uint`	将图像转换为 16 位无符号整数格式。
`invert`	反转图像。
`label_points`	为图像掩码上的坐标分配唯一的整数标签
`lookfor`	在 scikit-image 文档字符串上执行关键字搜索并打印结果。
`map_array`	将输入数组中的值从 input_vals 映射到 output_vals。
`montage`	创建多个单通道或多通道图像的蒙太奇。
`random_noise`	用于向浮点图像添加各种类型的随机噪声的函数。
`regular_grid`	查找沿 `ar_shape` 规则间隔的 `n_points`。
`regular_seeds`	返回具有 ~`n_points` 个规则间隔的非零像素的图像。
`slice_along_axes`	沿给定轴切片图像。
`unique_rows`	从 2D 数组中删除重复的行。
`view_as_blocks`	输入 n 维数组的块视图（使用重步幅）。
`view_as_windows`	输入 n 维数组的滚动窗口视图。

skimage.util.apply_parallel(function, array, chunks=None, depth=0, mode=None, extra_arguments=(), extra_keywords=None, *, dtype=None, compute=None, channel_axis=None)[源代码]#

在数组上并行映射函数。

将数组拆分为给定深度和边界类型的可能重叠的块，并行调用块上的给定函数，组合块并返回结果数组。

参数:

function函数: 要映射的函数，它将数组作为参数。
arraynumpy 数组或 dask 数组: 将应用该函数的数组。
chunksint、tuple 或 tuple 的 tuple，可选: 单个整数被解释为应该在数组上平铺的方形块的一边的长度。长度为 array.ndim 的一个元组表示块的形状，并在数组上平铺。长度为 ndim 的元组列表，其中每个子元组是沿相应维度的块大小的序列。如果为 None，则根据可用 cpu 的数量将数组分解为块。有关块的更多信息，请参阅此处的文档。当 channel_axis 不为 None 时，元组的长度可以为 ndim - 1，并且将沿通道轴使用单个块。
depthint 或 int 序列，可选: 添加的边界单元格的深度。可以使用元组来指定每个数组轴的不同深度。默认为零。当 channel_axis 不为 None，并且提供了长度为 ndim - 1 的元组时，将沿通道轴使用深度 0。
mode{‘reflect’、‘symmetric’、‘periodic’、‘wrap’、‘nearest’、‘edge’}，可选: 外部边界填充的类型。
extra_arguments元组，可选: 要传递给函数的参数的元组。
extra_keywords字典，可选: 要传递给函数的关键字参数的字典。
dtype数据类型或 None，可选: function 输出的数据类型。如果为 None，则 Dask 将尝试通过在形状为 (1,) * ndim 的数据上调用该函数来推断此数据类型。对于预期 RGB 或多通道数据的函数，这可能存在问题。在这种情况下，用户应手动指定此 dtype 参数。

在 0.18 版本中添加：在 0.18 中添加了 dtype。
computebool，可选: 如果为 True，则立即计算并返回 NumPy 数组。如果为 False，则延迟计算并返回 Dask 数组。如果为 None（默认），则根据提供的数组类型进行计算（对于 NumPy 数组立即计算，对于 Dask 数组延迟计算）。
channel_axisint 或 None，可选: 如果为 None，则假定图像为灰度（单通道）图像。否则，此参数指示数组的哪个轴对应于通道。

返回:

outndarray 或 dask 数组: 返回应用操作的结果。类型取决于 compute 参数。

注释

Numpy 边缘模式“symmetric”、“wrap”和“edge”转换为等效的 dask 边界模式“reflect”、“periodic”和“nearest”。设置 compute=False 对于链接以后的操作很有用。例如，用于预览结果的区域选择或将大数据存储到磁盘而不是加载到内存中。

skimage.util.compare_images(image0, image1, *, method='diff', n_tiles=(8, 8))[源代码]#

返回显示两幅图像之间差异的图像。

在 0.16 版本中添加。

参数:

image0，image1ndarray，形状 (M, N): 要处理的图像，必须具有相同的形状。

在 0.24 版本中更改：image1 和 image2 分别重命名为 image0 和 image1。
method字符串，可选: 用于比较的方法。有效值为 {‘diff’、‘blend’、‘checkerboard’}。详细信息在注释部分中提供。

在 0.24 版本中更改：此参数和以下参数仅为关键字参数。
n_tiles元组，可选: 仅用于 checkerboard 方法。指定用于划分图像的瓦片（行、列）的数量。

返回:

comparisonndarray，形状 (M, N): 显示差异的图像。

注释

'diff' 计算两幅图像之间的绝对差值。'blend' 计算平均值。'checkerboard' 创建维度为 n_tiles 的瓦片，交替显示第一幅和第二幅图像。请注意，要使用棋盘格方法进行比较，图像必须是二维的。

边缘算子

可视化图像比较

skimage.util.crop(ar, crop_width, copy=False, order='K')[source]#

沿每个维度将数组 ar 裁剪 crop_width。

参数:

ar类数组，秩为 N: 输入数组。
crop_width{序列, int}: 从每个轴的边缘移除的值的数量。((before_1, after_1), … (before_N, after_N)) 指定每个轴的开始和结束处的唯一裁剪宽度。((before, after),) 或 (before, after) 指定每个轴固定的开始和结束裁剪。(n,) 或整数 n 的 n 是所有轴的 before = after = n 的简写。
copybool, 可选: 如果 True，确保返回的数组是一个连续的副本。通常，裁剪操作将返回底层输入数组的不连续视图。
order{‘C’, ‘F’, ‘A’, ‘K’}, 可选: 如果 copy==True，控制副本的内存布局。请参阅 np.copy。

返回:

cropped数组: 裁剪后的数组。如果 copy=False（默认），这是输入数组的切片视图。

skimage.util.dtype_limits(image, clip_negative=False)[source]#

返回图像的 dtype 的强度限制，即 (最小值, 最大值) 元组。

参数:

imagendarray: 输入图像。
clip_negativebool, 可选: 如果为 True，即使图像 dtype 允许负值，也会剪切负范围（即，对于最小强度返回 0）。

返回:

imin, imax元组: 下限和上限强度限制。

skimage.util.img_as_bool(image, force_copy=False)[source]#

将图像转换为布尔格式。

参数:

imagendarray: 输入图像。
force_copybool, 可选: 强制复制数据，而与其当前 dtype 无关。

返回:

outbool 类型的 ndarray (bool_): 输出图像。

注释

输入 dtype 的正范围的上半部分为 True，下半部分为 False。所有负值（如果存在）均为 False。

skimage.util.img_as_float(image, force_copy=False)[source]#

将图像转换为浮点格式。

此函数类似于 img_as_float64，但不会将较低精度的浮点数组转换为 float64。

参数:

imagendarray: 输入图像。
force_copybool, 可选: 强制复制数据，而与其当前 dtype 无关。

返回:

outfloat 类型的 ndarray: 输出图像。

注释

浮点图像的范围是 [0.0, 1.0] 或 [-1.0, 1.0]，当分别从无符号或有符号数据类型转换时。如果输入图像具有浮点类型，则强度值不会被修改，并且可以在范围 [0.0, 1.0] 或 [-1.0, 1.0] 之外。

skimage.util.img_as_float32(image, force_copy=False)[source]#

将图像转换为单精度（32 位）浮点格式。

参数:

imagendarray: 输入图像。
force_copybool, 可选: 强制复制数据，而与其当前 dtype 无关。

返回:

outfloat32 类型的 ndarray: 输出图像。

注释

浮点图像的范围是 [0.0, 1.0] 或 [-1.0, 1.0]，当分别从无符号或有符号数据类型转换时。如果输入图像具有浮点类型，则强度值不会被修改，并且可以在范围 [0.0, 1.0] 或 [-1.0, 1.0] 之外。

skimage.util.img_as_float64(image, force_copy=False)[source]#

将图像转换为双精度（64 位）浮点格式。

参数:

imagendarray: 输入图像。
force_copybool, 可选: 强制复制数据，而与其当前 dtype 无关。

返回:

outfloat64 类型的 ndarray: 输出图像。

注释

浮点图像的范围是 [0.0, 1.0] 或 [-1.0, 1.0]，当分别从无符号或有符号数据类型转换时。如果输入图像具有浮点类型，则强度值不会被修改，并且可以在范围 [0.0, 1.0] 或 [-1.0, 1.0] 之外。

skimage.util.img_as_int(image, force_copy=False)[source]#

将图像转换为 16 位有符号整数格式。

参数:

imagendarray: 输入图像。
force_copybool, 可选: 强制复制数据，而与其当前 dtype 无关。

返回:

outint16 类型的 ndarray: 输出图像。

注释

这些值在 -32768 和 32767 之间缩放。如果输入数据类型是仅正值（例如，uint8），则输出图像仍然只有正值。

skimage.util.img_as_ubyte(image, force_copy=False)[source]#

将图像转换为 8 位无符号整数格式。

参数:

imagendarray: 输入图像。
force_copybool, 可选: 强制复制数据，而与其当前 dtype 无关。

返回:

outubyte (uint8) 类型的 ndarray: 输出图像。

注释

负的输入值将被裁剪。正值在 0 到 255 之间缩放。

skimage.util.img_as_uint(image, force_copy=False)[source]#

将图像转换为 16 位无符号整数格式。

参数:

imagendarray: 输入图像。
force_copybool, 可选: 强制复制数据，而与其当前 dtype 无关。

返回:

outuint16 类型的 ndarray: 输出图像。

注释

负的输入值将被裁剪。正值在 0 到 65535 之间缩放。

skimage.util.invert(image, signed_float=False)[source]#

反转图像。

反转输入图像的强度范围，使 dtype 的最大值现在成为 dtype 的最小值，反之亦然。此操作根据输入 dtype 略有不同

无符号整数：从 dtype 最大值中减去图像
有符号整数：从 -1 中减去图像（请参阅注释）
浮点数：从 1 中减去图像（如果 signed_float 为 False，因此我们假设图像是无符号的），或者从 0 中减去图像（如果 signed_float 为 True）。

请参阅示例以进行澄清。

参数:

imagendarray: 输入图像。
signed_floatbool, 可选: 如果为 True 且图像类型为 float，则假定范围为 [-1, 1]。如果为 False 且图像类型为 float，则假定范围为 [0, 1]。

返回:

invertedndarray: 反转后的图像。

注释

理想情况下，对于有符号整数，我们只需乘以 -1。但是，有符号整数范围是不对称的。例如，对于 np.int8，可能值的范围是 [-128, 127]，因此 -128 * -1 等于 -128！通过从 -1 中减去，我们正确地将最大 dtype 值映射到最小值。

示例

>>> img = np.array([[100,  0, 200],
...                 [  0, 50,   0],
...                 [ 30,  0, 255]], np.uint8)
>>> invert(img)
array([[155, 255,  55],
       [255, 205, 255],
       [225, 255,   0]], dtype=uint8)
>>> img2 = np.array([[ -2, 0, -128],
...                  [127, 0,    5]], np.int8)
>>> invert(img2)
array([[   1,   -1,  127],
       [-128,   -1,   -6]], dtype=int8)
>>> img3 = np.array([[ 0., 1., 0.5, 0.75]])
>>> invert(img3)
array([[1.  , 0.  , 0.5 , 0.25]])
>>> img4 = np.array([[ 0., 1., -1., -0.25]])
>>> invert(img4, signed_float=True)
array([[-0.  , -1.  ,  1.  ,  0.25]])

凸包

骨架化

使用滚动球算法估计背景强度

skimage.util.label_points(coords, output_shape)[source]#

为图像掩码上的坐标分配唯一的整数标签

参数:

coords: ndarray: 具有维度 D 的 N 个坐标的数组
output_shape: tuple: 在其上标记 coords 的掩模的形状

返回:

labels: ndarray: 包含 coords 处唯一整数标签的零掩模

注释

标签被分配给转换为整数并被认为从 0 开始的坐标。
超出掩模范围的坐标会引发 IndexError。
负坐标会引发 ValueError

示例

>>> import numpy as np
>>> from skimage.util._label import label_points
>>> coords = np.array([[0, 1], [2, 2]])
>>> output_shape = (5, 5)
>>> mask = label_points(coords, output_shape)
>>> mask
array([[0, 1, 0, 0, 0],
       [0, 0, 0, 0, 0],
       [0, 0, 2, 0, 0],
       [0, 0, 0, 0, 0],
       [0, 0, 0, 0, 0]], dtype=uint64)

skimage.util.lookfor(what)[source]#

在 scikit-image 文档字符串上执行关键字搜索并打印结果。

警告

此函数也可能打印不属于 scikit-image 公共 API 的结果。

参数:

whatstr: 要查找的词语。

示例

>>> import skimage as ski
>>> ski.util.lookfor('regular_grid')
Search results for 'regular_grid'
---------------------------------
skimage.util.regular_grid
    Find `n_points` regularly spaced along `ar_shape`.
skimage.util.lookfor
    Do a keyword search on scikit-image docstrings and print results.

skimage.util.map_array(input_arr, input_vals, output_vals, out=None)[源代码]#

将输入数组中的值从 input_vals 映射到 output_vals。

参数:

input_arr整数数组，形状 (M[, …]): 输入标签图像。
input_vals整数数组，形状 (K,): 要映射的源值。
output_vals数组，形状 (K,): 要映射到的目标值。
out: 数组，与 `input_arr` 形状相同: 输出数组。如果未提供，则将创建它。它应具有与 output_vals 相同的数据类型。

返回:

out数组，与 input_arr 形状相同: 映射值的数组。

注释

如果 input_arr 包含 input_vals 未涵盖的值，则将它们设置为 0。

示例

>>> import numpy as np
>>> import skimage as ski
>>> ski.util.map_array(
...    input_arr=np.array([[0, 2, 2, 0], [3, 4, 5, 0]]),
...    input_vals=np.array([1, 2, 3, 4, 6]),
...    output_vals=np.array([6, 7, 8, 9, 10]),
... )
array([[0, 7, 7, 0],
       [8, 9, 0, 0]])

skimage.util.montage(arr_in, fill='mean', rescale_intensity=False, grid_shape=None, padding_width=0, *, channel_axis=None)[源代码]#

创建多个单通道或多通道图像的蒙太奇。

从代表等形状的单通道（灰度）或多通道（彩色）图像集合的输入数组创建矩形蒙太奇。

例如，使用以下 arr_in 调用 montage(arr_in)

1

2

3

将返回

1	2
3

其中 “*” 补丁将由 fill 参数确定。

参数:

arr_inndarray，形状 (K, M, N[, C]): 表示 K 个形状相同的图像集合的数组。
fill浮点数或类数组浮点数，或 ‘mean’，可选: 用于填充填充区域和/或输出数组中额外图块的值。对于单通道集合，必须为 float。对于多通道集合，必须是形状为通道数的类数组。如果为 mean，则使用所有图像的平均值。
rescale_intensitybool，可选: 是否将每个图像的强度重新缩放到 [0, 1]。
grid_shapetuple，可选: 蒙太奇所需的网格形状 (ntiles_row, ntiles_column)。默认纵横比为正方形。
padding_widthint，可选: 图块之间以及图块与边界之间的间距大小。如果非零，则更容易感知单个图像的边界。
channel_axisint 或 None，可选: 如果为 None，则假定图像为灰度（单通道）图像。否则，此参数指示数组的哪个轴对应于通道。

返回:

arr_out(K*(M+p)+p, K*(N+p)+p[, C]) ndarray: 将输入图像粘合在一起的输出数组（包括填充 p）。

示例

>>> import numpy as np
>>> from skimage.util import montage
>>> arr_in = np.arange(3 * 2 * 2).reshape(3, 2, 2)
>>> arr_in  
array([[[ 0,  1],
        [ 2,  3]],
       [[ 4,  5],
        [ 6,  7]],
       [[ 8,  9],
        [10, 11]]])
>>> arr_out = montage(arr_in)
>>> arr_out.shape
(4, 4)
>>> arr_out
array([[ 0,  1,  4,  5],
       [ 2,  3,  6,  7],
       [ 8,  9,  5,  5],
       [10, 11,  5,  5]])
>>> arr_in.mean()
5.5
>>> arr_out_nonsquare = montage(arr_in, grid_shape=(1, 3))
>>> arr_out_nonsquare
array([[ 0,  1,  4,  5,  8,  9],
       [ 2,  3,  6,  7, 10, 11]])
>>> arr_out_nonsquare.shape
(2, 6)

来自图像的 Gabor / 初级视觉皮层“简单细胞”

探索 3D 图像（细胞的）

skimage.util.random_noise(image, mode='gaussian', rng=None, clip=True, **kwargs)[源代码]#

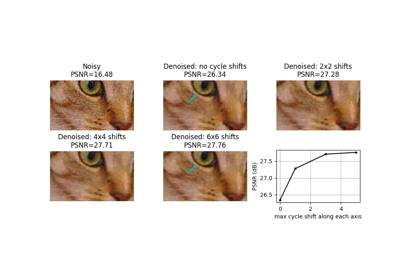
用于向浮点图像添加各种类型的随机噪声的函数。

参数:

imagendarray

输入图像数据。将转换为浮点数。

modestr，可选

以下字符串之一，选择要添加的噪声类型

“gaussian”（默认）: 高斯分布的加性噪声。
“localvar”: 高斯分布的加性噪声，在 image 的每个点都具有指定的局部方差。
“poisson”: 从数据生成的泊松分布噪声。
“salt”: 将随机像素替换为 1。
“pepper”: 将随机像素替换为 0（对于无符号图像）或 -1（对于有符号图像）。
“s&p”: 将随机像素替换为 1 或 low_val，其中 low_val 对于无符号图像为 0，对于有符号图像为 -1。
“speckle”: 使用 out = image + n * image 的乘性噪声，其中 n 是具有指定均值和方差的高斯噪声。

rng{numpy.random.Generator, int}, optional

伪随机数生成器。默认情况下，使用 PCG64 生成器（请参阅 numpy.random.default_rng()）。如果 rng 是一个整数，则用于播种生成器。

clipbool，可选

如果为 True（默认），则在对 'speckle'、'poisson' 和 'gaussian' 模式应用噪声后，将裁剪输出。这是保持正确的图像数据范围所必需的。如果为 False，则不应用裁剪，并且输出可能会超出范围 [-1, 1]。

meanfloat，可选

随机分布的均值。在“gaussian”和“speckle”中使用。默认值：0。

varfloat，可选

随机分布的方差。在“gaussian”和“speckle”中使用。注意：方差 = (标准差) ** 2。默认值：0.01

local_varsndarray，可选

正浮点数数组，与 image 形状相同，定义每个图像点的局部方差。在“localvar”中使用。

amountfloat，可选

要用噪声替换的图像像素的比例，范围为 [0, 1]。在“salt”、“pepper”和“salt & pepper”中使用。默认值：0.05

salt_vs_pepperfloat，可选

“s&p”的盐噪声与胡椒噪声的比例，范围为 [0, 1]。更高的值表示更多的盐。默认值：0.5（等量）

返回:

outndarray: 如果输入 image 分别是无符号或有符号，则输出范围在 [0, 1] 或 [-1, 1] 的浮点图像数据。

注释

散斑、泊松、局部方差和高斯噪声可能会生成超出有效图像范围的噪声。默认设置是裁剪（不使用别名）这些值，但可以通过设置 clip=False 来保留它们。请注意，在这种情况下，输出可能包含超出范围 [0, 1] 或 [-1, 1] 的值。请谨慎使用此选项。

由于中间计算中主要使用正浮点图像，因此无法仅根据数据类型来推断输入是否有符号。相反，会显式搜索负值。只有找到负值，此函数才会假定输入为有符号。意外的结果仅发生在罕见的、暴露不良的情况下（例如，如果签名 image 中的所有值都高于 50% 的灰色）。在这种情况下，手动将输入缩放到正域将解决问题。

泊松分布仅针对正整数定义。要应用此噪声类型，将找到图像中唯一值的数量，并使用下一个四舍五入的 2 的幂来放大浮点结果，之后将其缩小到浮点图像范围。

要针对有符号图像生成泊松噪声，会将有符号图像临时转换为浮点域中的无符号图像，生成泊松噪声，然后将其返回到原始范围。

skimage.util.regular_grid(ar_shape, n_points)[源代码]#

查找沿 ar_shape 规则间隔的 n_points。

返回的点（作为切片）应尽可能接近立方间隔。本质上，这些点间隔为输入数组大小的 N 次方根，其中 N 是维数。但是，如果数组维度无法容纳完整的步长，则将其“丢弃”，并且仅对剩余维度执行计算。

参数:

ar_shape类数组整数: 嵌入网格的空间的形状。len(ar_shape) 是维数。
n_pointsint: 要嵌入空间中的（近似）点数。

返回:

slicesslice 对象元组

沿着 ar_shape 的每个维度的切片，使得所有切片的交点给出规则间隔的点的坐标。

在 0.14.1 版本中更改：在 scikit-image 0.14.1 和 0.15 中，为了确保与 Numpy 1.15 及更高版本的兼容性，返回类型从列表更改为元组。如果您的代码需要返回的结果是列表，您可以使用以下方法将此函数的输出转换为列表：

>>> result = list(regular_grid(ar_shape=(3, 20, 40), n_points=8))

示例

>>> ar = np.zeros((20, 40))
>>> g = regular_grid(ar.shape, 8)
>>> g
(slice(5, None, 10), slice(5, None, 10))
>>> ar[g] = 1
>>> ar.sum()
8.0
>>> ar = np.zeros((20, 40))
>>> g = regular_grid(ar.shape, 32)
>>> g
(slice(2, None, 5), slice(2, None, 5))
>>> ar[g] = 1
>>> ar.sum()
32.0
>>> ar = np.zeros((3, 20, 40))
>>> g = regular_grid(ar.shape, 8)
>>> g
(slice(1, None, 3), slice(5, None, 10), slice(5, None, 10))
>>> ar[g] = 1
>>> ar.sum()
8.0

使用紧凑分水岭查找规则分段

skimage.util.regular_seeds(ar_shape, n_points, dtype=<class 'int'>)[源代码]#

返回具有 ~`n_points` 个规则间隔的非零像素的图像。

参数:

ar_shape整数元组: 所需输出图像的形状。
n_pointsint: 所需的非零点数。
dtypenumpy 数据类型，可选: 所需的输出数据类型。

返回:

seed_img整数或布尔数组: 所需的图像。

示例

>>> regular_seeds((5, 5), 4)
array([[0, 0, 0, 0, 0],
       [0, 1, 0, 2, 0],
       [0, 0, 0, 0, 0],
       [0, 3, 0, 4, 0],
       [0, 0, 0, 0, 0]])

skimage.util.slice_along_axes(image, slices, axes=None, copy=False)[源代码]#

沿给定轴切片图像。

参数:

imagendarray: 输入图像。
slices2 元组列表 (a, b) 其中 a < b。: 对于 axes 中的每个轴，一个对应的 2 元组 (min_val, max_val) 用于切片（与 Python 切片一样，max_val 是非包含的）。
axes整数或元组，可选: 与 slices 中给定的限制对应的轴。如果为 None，则轴按升序排列，直到 slices 的长度。
copybool, 可选: 如果为 True，则确保输出不是 image 的视图。

返回:

outndarray: 与给定的切片和轴对应的 image 区域。

示例

>>> from skimage import data
>>> img = data.camera()
>>> img.shape
(512, 512)
>>> cropped_img = slice_along_axes(img, [(0, 100)])
>>> cropped_img.shape
(100, 512)
>>> cropped_img = slice_along_axes(img, [(0, 100), (0, 100)])
>>> cropped_img.shape
(100, 100)
>>> cropped_img = slice_along_axes(img, [(0, 100), (0, 75)], axes=[1, 0])
>>> cropped_img.shape
(75, 100)

skimage.util.unique_rows(ar)[源代码]#

从 2D 数组中删除重复的行。

特别地，如果给定一个形状为 (Npoints, Ndim) 的坐标数组，它将删除重复的点。

参数:

arndarray，形状 (M, N): 输入数组。

返回:

ar_outndarray，形状 (P, N): 删除重复行的输入数组的副本。

引发:

ValueError如果 ar 不是二维的。

注释

如果 ar 不是 C 连续的，该函数将生成它的副本，这将对大型输入数组的性能产生负面影响。

示例

>>> ar = np.array([[1, 0, 1],
...                [0, 1, 0],
...                [1, 0, 1]], np.uint8)
>>> unique_rows(ar)
array([[0, 1, 0],
       [1, 0, 1]], dtype=uint8)

skimage.util.view_as_blocks(arr_in, block_shape)[源代码]#

输入 n 维数组的块视图（使用重步幅）。

块是输入数组的非重叠视图。

参数:

arr_inndarray，形状 (M[, …]): 输入数组。
block_shape元组: 块的形状。每个维度必须均匀地除以 arr_in 的相应维度。

返回:

arr_outndarray: 输入数组的块视图。

示例

>>> import numpy as np
>>> from skimage.util.shape import view_as_blocks
>>> A = np.arange(4*4).reshape(4,4)
>>> A
array([[ 0,  1,  2,  3],
       [ 4,  5,  6,  7],
       [ 8,  9, 10, 11],
       [12, 13, 14, 15]])
>>> B = view_as_blocks(A, block_shape=(2, 2))
>>> B[0, 0]
array([[0, 1],
       [4, 5]])
>>> B[0, 1]
array([[2, 3],
       [6, 7]])
>>> B[1, 0, 1, 1]
13

>>> A = np.arange(4*4*6).reshape(4,4,6)
>>> A  
array([[[ 0,  1,  2,  3,  4,  5],
        [ 6,  7,  8,  9, 10, 11],
        [12, 13, 14, 15, 16, 17],
        [18, 19, 20, 21, 22, 23]],
       [[24, 25, 26, 27, 28, 29],
        [30, 31, 32, 33, 34, 35],
        [36, 37, 38, 39, 40, 41],
        [42, 43, 44, 45, 46, 47]],
       [[48, 49, 50, 51, 52, 53],
        [54, 55, 56, 57, 58, 59],
        [60, 61, 62, 63, 64, 65],
        [66, 67, 68, 69, 70, 71]],
       [[72, 73, 74, 75, 76, 77],
        [78, 79, 80, 81, 82, 83],
        [84, 85, 86, 87, 88, 89],
        [90, 91, 92, 93, 94, 95]]])
>>> B = view_as_blocks(A, block_shape=(1, 2, 2))
>>> B.shape
(4, 2, 3, 1, 2, 2)
>>> B[2:, 0, 2]  
array([[[[52, 53],
         [58, 59]]],
       [[[76, 77],
         [82, 83]]]])

图像/数组的块视图

skimage.util.view_as_windows(arr_in, window_shape, step=1)[源代码]#

输入 n 维数组的滚动窗口视图。

窗口是输入数组的重叠视图，相邻窗口移动一行或一列（或更高维度的索引）。

参数:

arr_inndarray，形状 (M[, …]): 输入数组。
window_shape整数或长度为 arr_in.ndim 的元组: 定义滚动窗口视图的基本 n 维正交体（更广为人知的是超矩形 [1]）的形状。如果给定整数，则形状将是由其值给出的边长的超立方体。
step整数或长度为 arr_in.ndim 的元组: 指示执行提取的步长。如果给定整数，则步长在所有维度上都是均匀的。

返回:

arr_outndarray: 输入数组的（滚动）窗口视图。

注释

在内存使用方面，应该非常小心滚动视图。事实上，虽然“视图”与它的基础数组具有相同的内存占用，但是当在计算中使用此“视图”时出现的实际数组通常比原始数组大得多（很多），特别是对于二维及以上的数组。

例如，让我们考虑一个大小为 (100, 100, 100) 的 float64 三维数组。此数组占用大约 8 * 100**3 字节的存储空间，只有 8 MB。如果决定在此数组上构建一个窗口为 (3, 3, 3) 的滚动视图，则滚动视图的假设大小（如果要例如重塑视图）将为 8 * (100-3+1)**3 * 3**3，约为 203 MB！随着输入数组的维度变大，缩放变得更加糟糕。

参考文献

[1]

https://en.wikipedia.org/wiki/Hyperrectangle

示例

>>> import numpy as np
>>> from skimage.util.shape import view_as_windows
>>> A = np.arange(4*4).reshape(4,4)
>>> A
array([[ 0,  1,  2,  3],
       [ 4,  5,  6,  7],
       [ 8,  9, 10, 11],
       [12, 13, 14, 15]])
>>> window_shape = (2, 2)
>>> B = view_as_windows(A, window_shape)
>>> B[0, 0]
array([[0, 1],
       [4, 5]])
>>> B[0, 1]
array([[1, 2],
       [5, 6]])

>>> A = np.arange(10)
>>> A
array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
>>> window_shape = (3,)
>>> B = view_as_windows(A, window_shape)
>>> B.shape
(8, 3)
>>> B
array([[0, 1, 2],
       [1, 2, 3],
       [2, 3, 4],
       [3, 4, 5],
       [4, 5, 6],
       [5, 6, 7],
       [6, 7, 8],
       [7, 8, 9]])

>>> A = np.arange(5*4).reshape(5, 4)
>>> A
array([[ 0,  1,  2,  3],
       [ 4,  5,  6,  7],
       [ 8,  9, 10, 11],
       [12, 13, 14, 15],
       [16, 17, 18, 19]])
>>> window_shape = (4, 3)
>>> B = view_as_windows(A, window_shape)
>>> B.shape
(2, 2, 4, 3)
>>> B  
array([[[[ 0,  1,  2],
         [ 4,  5,  6],
         [ 8,  9, 10],
         [12, 13, 14]],
        [[ 1,  2,  3],
         [ 5,  6,  7],
         [ 9, 10, 11],
         [13, 14, 15]]],
       [[[ 4,  5,  6],
         [ 8,  9, 10],
         [12, 13, 14],
         [16, 17, 18]],
        [[ 5,  6,  7],
         [ 9, 10, 11],
         [13, 14, 15],
         [17, 18, 19]]]])

来自图像的 Gabor / 初级视觉皮层“简单细胞”

skimage.util#

`skimage.util`#