skimage.restoration#
复原算法,例如,反卷积算法、去噪等。
为 restoration.rolling_ball 创建球形核。 |
|
校准去噪函数并返回最佳 J 不变版本。 |
|
循环旋转(将 func 重复应用于 x 的移位版本)。 |
|
使用双边滤波器对图像进行去噪。 |
|
应用去噪函数的 J 不变版本。 |
|
对 2D-4D 灰度或 RGB 图像执行非局部均值去噪。 |
|
使用 split-Bregman 优化执行总变分去噪。 |
|
在 nD 中执行总变分去噪。 |
|
对图像执行小波去噪。 |
|
为 restoration.rolling_ball 创建椭球形核。 |
|
(高斯)噪声标准偏差的稳健的基于小波的估计器。 |
|
使用双调和方程修补图像中被遮盖的点。 |
|
理查森-露西反卷积。 |
|
通过滚动/平移内核来估计背景强度。 |
|
无监督维纳-亨特反卷积。 |
|
从包裹的相位图像中恢复原始图像。 |
|
维纳-亨特反卷积 |
- skimage.restoration.ball_kernel(radius, ndim)[source]#
为 restoration.rolling_ball 创建球形核。
- 参数:
- radiusint
球的半径。
- ndimint
球的维度数。
ndim应与将应用内核的图像的维度匹配。
- 返回:
- kernelndarray
包含椭球上半部分的表面强度的内核。
另请参阅
- skimage.restoration.calibrate_denoiser(image, denoise_function, denoise_parameters, *, stride=4, approximate_loss=True, extra_output=False)[source]#
校准去噪函数并返回最佳 J 不变版本。
返回的函数使用为去噪输入图像设置的最佳参数值进行部分评估。
- 参数:
- imagendarray
要进行去噪的输入数据(使用
img_as_float转换)。- denoise_functionfunction
要校准的去噪函数。
- denoise_parametersdict of list
要校准的
denoise_function的参数范围。- strideint, optional
在将
denoise_function转换为 J 不变性的遮罩过程中使用的步幅。- approximate_lossbool, optional
是否通过仅在图像的一个遮罩版本上计算来自评估去噪器的自监督损失。 如果为 False,则运行时间将增加
stride**image.ndim倍。- extra_outputbool, optional
如果为 True,则除了校准的去噪函数之外,还会返回参数和损失
- 返回:
- best_denoise_functionfunction
denoise_function的最佳 J 不变版本。- 如果
extra_output为 True,则还会返回以下元组 - (parameters_tested, losses)tuple (list of dict, list of int)
为
denoise_function测试的参数列表,作为 kwargs 的字典parameters_tested中每个参数集的自监督损失。
备注
校准过程使用自监督均方误差损失来评估
denoise_function的 J 不变版本的性能。 自监督损失的最小化器也是真实损失(即真实的 MSE 误差)的最小化器 [1]。 返回的函数可用于原始噪声图像或具有相似特征的其他图像。- 增加步幅会提高
best_denoise_function的性能 但会增加其运行时间。 它对校准的运行时间没有影响。
参考文献
[1]J. Batson & L. Royer。 Noise2Self:通过自监督进行盲去噪,国际机器学习会议,第 524-533 页(2019 年)。
示例
>>> from skimage import color, data >>> from skimage.restoration import denoise_tv_chambolle >>> import numpy as np >>> img = color.rgb2gray(data.astronaut()[:50, :50]) >>> rng = np.random.default_rng() >>> noisy = img + 0.5 * img.std() * rng.standard_normal(img.shape) >>> parameters = {'weight': np.arange(0.01, 0.3, 0.02)} >>> denoising_function = calibrate_denoiser(noisy, denoise_tv_chambolle, ... denoise_parameters=parameters) >>> denoised_img = denoising_function(img)
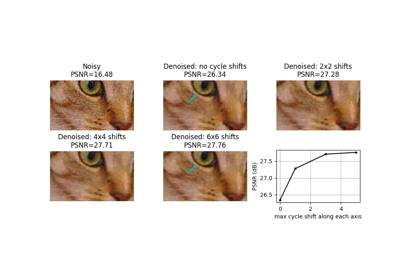
- skimage.restoration.cycle_spin(x, func, max_shifts, shift_steps=1, num_workers=None, func_kw=None, *, channel_axis=None)[source]#
循环旋转(将 func 重复应用于 x 的移位版本)。
- 参数:
- xarray-like
输入到
func的数据。- funcfunction
要应用于
x的循环移位版本的函数。应将x作为其第一个参数。任何其他参数都可以通过func_kw提供。- max_shiftsint 或 tuple
如果为整数,则将沿
x的每个轴使用range(0, max_shifts+1)中的移位。 如果为元组,则沿轴 i 使用range(0, max_shifts[i]+1)。- shift_stepsint 或 tuple, optional
沿轴 i 应用的移位的步长为::
range((0, max_shifts[i]+1, shift_steps[i]))。如果提供一个整数,则所有轴都使用相同的步长。- num_workersint 或 None, optional
在循环旋转期间使用的并行线程数。如果设置为
None,则使用所有可用的内核。- func_kwdict, optional
要提供给
func的其他关键字参数。- channel_axisint 或 None, optional
如果为 None,则假定图像为灰度(单通道)图像。否则,此参数指示数组的哪个轴对应于通道。
0.19 版本中添加:在 0.19 中添加了
channel_axis。
- 返回:
- avg_ynp.ndarray
func(x, **func_kw)的输出在指定轴移位的所有组合上取平均值。
备注
循环旋转被提出作为一种通过执行移位变化变换 [1] 的若干循环移位来接近移位不变性的方法。
对于 n 级离散小波变换,可能希望执行所有位移,最大位移量为
max_shifts = 2**n - 1。但在实践中,通常只需对每个轴进行少量位移即可实现大部分好处。对于诸如分块离散余弦变换之类的变换,可能希望评估的位移量不超过变换所使用的块大小。
参考文献
[1]R.R. Coifman 和 D.L. Donoho。“Translation-Invariant De-Noising”。《Wavelets and Statistics》,Lecture Notes in Statistics,第 103 卷。Springer,纽约,1995 年,第 125-150 页。DOI:10.1007/978-1-4612-2544-7_9
示例
>>> import skimage.data >>> from skimage import img_as_float >>> from skimage.restoration import denoise_tv_chambolle, cycle_spin >>> img = img_as_float(skimage.data.camera()) >>> sigma = 0.1 >>> img = img + sigma * np.random.standard_normal(img.shape) >>> denoised = cycle_spin(img, func=denoise_tv_chambolle, ... max_shifts=3)
- skimage.restoration.denoise_bilateral(image, win_size=None, sigma_color=None, sigma_spatial=1, bins=10000, mode='constant', cval=0, *, channel_axis=None)[source]#
使用双边滤波器对图像进行去噪。
- 参数:
- imagendarray,形状 (M, N[, 3])
输入图像,2D 灰度或 RGB。
- win_sizeint
用于滤波的窗口大小。如果未指定 win_size,则将其计算为
max(5, 2 * ceil(3 * sigma_spatial) + 1)。- sigma_colorfloat
灰度值/颜色距离(辐射相似度)的标准偏差。值越大,则辐射差异较大的像素平均值越大。如果为
None,则将使用image的标准偏差。- sigma_spatialfloat
范围距离的标准偏差。值越大,则空间差异较大的像素平均值越大。
- binsint
颜色滤波的高斯权重的离散值数量。值越大,准确性越高。
- mode{‘constant’,‘edge’,‘symmetric’,‘reflect’,‘wrap’}
如何处理图像边界外的值。有关详细信息,请参阅
numpy.pad。- cvalint 或 float
与模式“constant”结合使用,表示图像边界外的值。
- channel_axisint 或 None, optional
如果为
None,则假定图像为灰度(单通道)。否则,此参数指示数组的哪个轴对应于通道。0.19 版本中添加:在 0.19 中添加了
channel_axis。
- 返回:
- denoisedndarray
去噪后的图像。
备注
这是一种保留边缘的去噪滤波器。它基于像素的空间接近度和辐射相似度来平均像素 [1]。
空间接近度是通过两个像素之间的欧几里得距离和一定的标准偏差(
sigma_spatial)的高斯函数来测量的。辐射相似度是通过两个颜色值之间的欧几里得距离和一定的标准偏差(
sigma_color)的高斯函数来测量的。请注意,如果图像的 dtype 为任何
int类型,则将使用img_as_float函数转换image,因此标准偏差 (sigma_color) 的范围将在[0, 1]内。有关 scikit-image 数据类型转换以及在这些转换中如何重新缩放图像的更多信息,请参阅:https://scikit-image.cn/docs/stable/user_guide/data_types.html。
参考文献
[1]C. Tomasi 和 R. Manduchi。“Bilateral Filtering for Gray and Color Images.”。IEEE International Conference on Computer Vision (1998) 839-846. DOI:10.1109/ICCV.1998.710815
示例
>>> from skimage import data, img_as_float >>> astro = img_as_float(data.astronaut()) >>> astro = astro[220:300, 220:320] >>> rng = np.random.default_rng() >>> noisy = astro + 0.6 * astro.std() * rng.random(astro.shape) >>> noisy = np.clip(noisy, 0, 1) >>> denoised = denoise_bilateral(noisy, sigma_color=0.05, sigma_spatial=15, ... channel_axis=-1)
- skimage.restoration.denoise_invariant(image, denoise_function, *, stride=4, masks=None, denoiser_kwargs=None)[source]#
应用去噪函数的 J 不变版本。
- 参数:
- imagendarray (M[, N[, …]][, C]),类型为 int、uint 或 float
要进行去噪的输入数据。
image可以是任何数字类型,但为了计算去噪后的图像,会将其转换为浮点类型的 ndarray(使用img_as_float)。- denoise_functionfunction
原始去噪函数。
- strideint, optional
在将
denoise_function转换为 J 不变性的遮罩过程中使用的步幅。- masksndarray 列表,可选
用于计算 J 不变输出的掩码集。如果为
None,将使用覆盖图像的完整掩码集。- denoiser_kwargs
传递给
denoise_function的关键字参数。
- 返回:
- outputndarray
去噪后的图像,形状与
image相同。
备注
如果去噪函数对每个像素的预测不依赖于原始图像中该像素的值,则该去噪函数是 J 不变的。相反,每个像素的预测可以使用图像其余部分中包含的所有相关信息,这通常非常重要。可以使用简单的掩码程序将任何函数转换为 J 不变的函数,如 [1] 中所述。
只要每个像素中的噪声是独立的,J 不变去噪器的逐像素误差就与噪声不相关。因此,去噪图像和有噪声图像之间的平均差异(即*自监督损失*)与去噪图像和原始干净图像之间的差异(即*真实损失*)相同(直到一个常数)。
这意味着可以使用有噪声的数据单独找到给定图像的最佳 J 不变去噪器,方法是选择最小化自监督损失的去噪器。
参考文献
[1]J. Batson & L. Royer。 Noise2Self:通过自监督进行盲去噪,国际机器学习会议,第 524-533 页(2019 年)。
示例
>>> import skimage >>> from skimage.restoration import denoise_invariant, denoise_tv_chambolle >>> image = skimage.util.img_as_float(skimage.data.chelsea()) >>> noisy = skimage.util.random_noise(image, var=0.2 ** 2) >>> denoised = denoise_invariant(noisy, denoise_function=denoise_tv_chambolle)
- skimage.restoration.denoise_nl_means(image, patch_size=7, patch_distance=11, h=0.1, fast_mode=True, sigma=0.0, *, preserve_range=False, channel_axis=None)[source]#
对 2D-4D 灰度或 RGB 图像执行非局部均值去噪。
- 参数:
- image2D 或 3D ndarray
要进行去噪的输入图像,可以是 2D 或 3D,并且可以是灰度或 RGB(仅适用于 2D 图像,请参阅
channel_axis参数)。可以有任意数量的通道(不一定必须是 RGB)。- patch_sizeint,可选
用于去噪的块大小。
- patch_distanceint,可选
搜索用于去噪的块的最大像素距离。
- hfloat,可选
截止距离(以灰度级表示)。h 越大,接受块的容忍度就越高。h 越大,图像越平滑,但会以模糊特征为代价。对于标准偏差为 sigma 的高斯噪声,经验法则是选择略小于 sigma 的 h 值。
- fast_modebool,可选
如果为 True(默认值),则使用非局部均值算法的快速版本。如果为 False,则使用非局部均值的原始版本。有关算法的更多详细信息,请参阅“注释”部分。
- sigmafloat,可选
(高斯)噪声的标准差。如果提供此参数,则会计算更稳健的块权重,其中会考虑预期的噪声方差(请参阅下面的“备注”)。
- preserve_rangebool,可选
是否保留原始值范围。否则,将根据
img_as_float的约定转换输入图像。另请参阅 https://scikit-image.cn/docs/dev/user_guide/data_types.html- channel_axisint 或 None, optional
如果为 None,则假定图像为灰度(单通道)图像。否则,此参数指示数组的哪个轴对应于通道。
0.19 版本中添加:在 0.19 中添加了
channel_axis。
- 返回:
- resultndarray
去噪后的图像,形状与
image相同。
备注
非局部均值算法非常适合对具有特定纹理的图像进行去噪。该算法的原理是将给定像素的值与有限邻域内其他像素的值进行平均,前提是围绕其他像素中心的块与围绕感兴趣像素中心的块足够相似。
在算法的原始版本 [1] 中,对应于
fast=False,计算复杂度为image.size * patch_size ** image.ndim * patch_distance ** image.ndim
因此,更改块的大小或它们的最大距离对计算时间有很大影响,特别是对于 3-D 图像。
但是,默认行为对应于
fast_mode=True,为此,使用了非局部均值的另一个版本 [2],对应的复杂度为image.size * patch_distance ** image.ndim
由于计算给定偏移的块距离的积分,减少了运算次数 [1],计算时间仅在很小程度上取决于块的大小。因此,此算法的执行速度比经典算法(
fast_mode=False)快,但代价是使用两倍的内存。此实现已被证明比其他替代方法更有效,例如,请参阅 [3]。与经典算法相比,块中的所有像素对到另一个块的距离的贡献权重相同,无论它们到块中心的距离如何。这种对距离的更粗略的计算可能导致去噪性能略差。此外,对于小图像(线性尺寸仅为块尺寸几倍的图像),由于边界效应,经典算法可能更快。
在去噪之前,使用
skimage.util.pad的reflect模式对图像进行填充。如果提供了噪声标准差
sigma,则会使用更稳健的块权重计算。从计算的块距离中减去已知的噪声方差可以改进块相似度的估计,从而适度提高去噪性能 [4]。在 [3] 中,它也被提及为算法快速变体的选项。当提供
sigma时,通常应使用较小的h以避免过度平滑。h的最佳值取决于图像内容和噪声水平,但是当fast_mode为True时,一个合理的起点是h = 0.8 * sigma,或者当fast_mode为False时,一个合理的起点是h = 0.6 * sigma。参考文献
[1] (1,2)A. Buades、B. Coll 和 J-M. Morel。一种用于图像去噪的非局部算法。在 CVPR 2005 中,第 2 卷,第 60-65 页,IEEE。 DOI:10.1109/CVPR.2005.38
[2]J. Darbon、A. Cunha、T.F. Chan、S. Osher 和 G.J. Jensen,《应用于电子低温显微镜的快速非局部滤波》,载于第五届 IEEE 国际生物医学成像研讨会:从纳米到宏观,2008 年,第 1331-1334 页。 DOI:10.1109/ISBI.2008.4541250
[3] (1,2)Jacques Froment。《无参数快速逐像素非局部均值去噪》。在线图像处理,2014 年,第 4 卷,第 300-326 页。 DOI:10.5201/ipol.2014.120
[4]A. Buades、B. Coll 和 J-M. Morel。《非局部均值去噪》。在线图像处理,2011 年,第 1 卷,第 208-212 页。 DOI:10.5201/ipol.2011.bcm_nlm
示例
>>> a = np.zeros((40, 40)) >>> a[10:-10, 10:-10] = 1. >>> rng = np.random.default_rng() >>> a += 0.3 * rng.standard_normal(a.shape) >>> denoised_a = denoise_nl_means(a, 7, 5, 0.1)
- skimage.restoration.denoise_tv_bregman(image, weight=5.0, max_num_iter=100, eps=0.001, isotropic=True, *, channel_axis=None)[来源]#
使用 split-Bregman 优化执行总变分去噪。
给定 \(f\),一个噪声图像(输入数据),全变分去噪(也称为全变分正则化)旨在找到一个全变分比 \(f\) 小的图像 \(u\),前提是 \(u\) 保持与 \(f\) 相似。这可以用 Rudin–Osher–Fatemi (ROF) 最小化问题表示
\[\min_{u} \sum_{i=0}^{N-1} \left( \left| \nabla{u_i} \right| + \frac{\lambda}{2}(f_i - u_i)^2 \right)\]其中 \(\lambda\) 是一个正参数。此成本函数的第一项是全变分;第二项表示数据保真度。当 \(\lambda \to 0\) 时,全变分项占主导地位,迫使解具有较小的全变分,但代价是看起来不太像输入数据。
此代码是 Goldstein 和 Osher 的分裂 Bregman 算法的实现,用于解决 ROF 问题 ([1]、[2]、[3])。
- 参数:
- imagendarray
要进行去噪的输入图像(使用
img_as_float()转换)。- weightfloat,可选
去噪权重。它等于 \(\frac{\lambda}{2}\)。因此,
weight越小,去噪效果越强(但代价是与image的相似度越低)。- epsfloat,可选
停止准则的容差 \(\varepsilon > 0\):当 \(\|u_n - u_{n-1}\|_2 < \varepsilon\) 时,算法停止。
- max_num_iterint,可选
用于优化的最大迭代次数。
- isotropicboolean,可选
在各向同性和各向异性 TV 去噪之间切换。
- channel_axisint 或 None, optional
如果为
None,则假定图像为灰度(单通道)。否则,此参数指示数组的哪个轴对应于通道。0.19 版本中添加:在 0.19 中添加了
channel_axis。
- 返回:
- undarray
去噪后的图像。
另请参阅
denoise_tv_chambolle在 nD 中执行总变分去噪。
备注
确保为彩色图像正确设置
channel_axis参数。全变分去噪的原理在 [4] 中进行了解释。它是关于最小化图像的全变分,这可以粗略地描述为图像梯度的范数的积分。全变分去噪倾向于产生卡通式图像,即分段恒定的图像。
参考文献
[1]Tom Goldstein 和 Stanley Osher,《用于 L1 正则化问题的分裂 Bregman 方法》,https://ww3.math.ucla.edu/camreport/cam08-29.pdf
[2]Pascal Getreuer,《使用分裂 Bregman 的 Rudin–Osher–Fatemi 全变分去噪》,载于 2012 年 5 月 19 日的在线图像处理,https://www.ipol.im/pub/art/2012/g-tvd/article_lr.pdf
- skimage.restoration.denoise_tv_chambolle(image, weight=0.1, eps=0.0002, max_num_iter=200, *, channel_axis=None)[来源]#
在 nD 中执行总变分去噪。
给定 \(f\),一个噪声图像(输入数据),全变分去噪(也称为全变分正则化)旨在找到一个全变分比 \(f\) 小的图像 \(u\),前提是 \(u\) 保持与 \(f\) 相似。这可以用 Rudin–Osher–Fatemi (ROF) 最小化问题表示
\[\min_{u} \sum_{i=0}^{N-1} \left( \left| \nabla{u_i} \right| + \frac{\lambda}{2}(f_i - u_i)^2 \right)\]其中 \(\lambda\) 是一个正参数。此成本函数的第一项是全变分;第二项表示数据保真度。当 \(\lambda \to 0\) 时,全变分项占主导地位,迫使解具有较小的全变分,但代价是看起来不太像输入数据。
此代码是 Chambolle 在 [1] 中提出的用于解决 ROF 问题的算法的实现。
- 参数:
- imagendarray
要进行去噪的输入图像。如果其 dtype 不是浮点数,则会使用
img_as_float()进行转换。- weightfloat,可选
去噪权重。它等于 \(\frac{1}{\lambda}\)。因此,
weight越大,去噪效果越强(但代价是与image的保真度越低)。- epsfloat,可选
停止准则的容差 \(\varepsilon > 0\)(与成本函数 \(E\) 的相对差异的绝对值进行比较):当 \(|E_{n-1} - E_n| < \varepsilon * E_0\) 时,算法停止。
- max_num_iterint,可选
用于优化的最大迭代次数。
- channel_axisint 或 None, optional
如果为
None,则假定图像为灰度(单通道)。否则,此参数指示数组的哪个轴对应于通道。0.19 版本中添加:在 0.19 中添加了
channel_axis。
- 返回:
- undarray
去噪后的图像。
另请参阅
denoise_tv_bregman使用 split-Bregman 优化执行总变分去噪。
备注
确保为彩色图像正确设置
channel_axis参数。全变分去噪的原理在 [2] 中进行了解释。它是关于最小化图像的全变分,这可以粗略地描述为图像梯度的范数的积分。全变分去噪倾向于产生卡通式图像,即分段恒定的图像。
参考文献
[1]A. Chambolle,《全变分最小化及其应用的算法》,数学成像和视觉杂志,Springer,2004 年,20,89-97。
示例
宇航员图像上的二维示例
>>> from skimage import color, data >>> img = color.rgb2gray(data.astronaut())[:50, :50] >>> rng = np.random.default_rng() >>> img += 0.5 * img.std() * rng.standard_normal(img.shape) >>> denoised_img = denoise_tv_chambolle(img, weight=60)
合成数据上的三维示例
>>> x, y, z = np.ogrid[0:20, 0:20, 0:20] >>> mask = (x - 22)**2 + (y - 20)**2 + (z - 17)**2 < 8**2 >>> mask = mask.astype(float) >>> rng = np.random.default_rng() >>> mask += 0.2 * rng.standard_normal(mask.shape) >>> res = denoise_tv_chambolle(mask, weight=100)
- skimage.restoration.denoise_wavelet(image, sigma=None, wavelet='db1', mode='soft', wavelet_levels=None, convert2ycbcr=False, method='BayesShrink', rescale_sigma=True, *, channel_axis=None)[source]#
对图像执行小波去噪。
- 参数:
- imagendarray (M[, N[, …P]][, C]),整数、无符号整数或浮点数类型
要进行去噪的输入数据。
image可以是任何数值类型,但在计算去噪图像时,它会被转换为浮点数类型的 ndarray。- sigma浮点数或列表,可选
计算小波细节系数阈值时使用的噪声标准差。当为 None (默认) 时,噪声标准差会通过 [2] 中的方法进行估计。
- wavelet字符串,可选
要执行的小波类型,可以是
pywt.wavelist输出的任何选项。 默认值为'db1'。 例如,wavelet可以是{'db2', 'haar', 'sym9'}以及更多。- mode{‘soft’, ‘hard’},可选
一个可选参数,用于选择执行的去噪类型。需要注意的是,在给定加性噪声的情况下,选择软阈值处理可以找到原始图像的最佳近似值。
- wavelet_levels整数或 None,可选
要使用的小波分解级别数。默认值比最大可能分解级别数少三个。
- convert2ycbcr布尔值,可选
如果为 True 并且设置了 channel_axis,则在 YCbCr 颜色空间而不是 RGB 颜色空间中进行小波去噪。 这通常会提高 RGB 图像的性能。
- method{‘BayesShrink’, ‘VisuShrink’},可选
要使用的阈值处理方法。 当前支持的方法是“BayesShrink” [1] 和 “VisuShrink” [2]。 默认为 “BayesShrink”。
- rescale_sigma布尔值,可选
如果为 False,则不会对用户提供的
sigma执行重新缩放。 默认值True会在内部重新缩放图像时适当重新缩放 sigma。0.16 版本中新增:
rescale_sigma在 0.16 版本中引入- channel_axisint 或 None, optional
如果为
None,则假定图像为灰度(单通道)。否则,此参数指示数组的哪个轴对应于通道。0.19 版本中添加:在 0.19 中添加了
channel_axis。
- 返回:
- outndarray
去噪后的图像。
备注
小波域是图像的稀疏表示,可以将其视为类似于傅里叶变换的频域。 稀疏表示的大部分值是零或接近于零,而真正的随机噪声(通常)由小波域中的许多小值表示。 将低于某个阈值的所有值设置为 0 可以减少图像中的噪声,但较大的阈值也会降低图像中存在的细节。
如果输入是 3D 的,则此函数会对每个颜色平面分别执行小波去噪。
在 0.16 版本中更改: 对于浮点数输入,将保留原始输入范围,并且不会对输出应用剪切。 其他输入类型将被转换为范围 [-1, 1] 或 [0, 1] 中的浮点数值,具体取决于输入图像范围。 除非
rescale_sigma = False,否则应用于image的任何内部重新缩放也将应用于sigma,以保持相同的相对幅度。已经提出了许多小波系数阈值处理方法。 默认情况下,
denoise_wavelet应用 BayesShrink,这是一种自适应阈值处理方法,它为每个小波子带计算单独的阈值,如 [1] 中所述。如果
method == "VisuShrink",则将单个“通用阈值”应用于所有小波细节系数,如 [2] 中所述。 此阈值旨在以高概率消除给定sigma下的所有高斯噪声,但往往会产生看起来过于平滑的图像。尽管可以选择
PyWavelets中的任何小波,但阈值处理方法假设正交小波变换,并且可能不会为双正交小波选择合适的阈值。 正交小波是可取的,因为输入中的白噪声在子带中仍然是白噪声。 双正交小波导致子带中的有色噪声。 此外,PyWavelets 中的正交小波是正交的,因此子带中的噪声方差与输入的噪声方差保持相同。 正交小波的示例是 Daubechies(例如 ‘db2’)或 symmlet(例如 ‘sym2’)系列。参考文献
[1] (1,2)Chang, S. Grace, Bin Yu, 和 Martin Vetterli。“用于图像去噪和压缩的自适应小波阈值处理。” Image Processing, IEEE Transactions on 9.9 (2000): 1532-1546. DOI:10.1109/83.862633
[2] (1,2,3)D. L. Donoho 和 I. M. Johnstone。“小波收缩的理想空间自适应。” Biometrika 81.3 (1994): 425-455. DOI:10.1093/biomet/81.3.425
示例
>>> from skimage import color, data >>> img = img_as_float(data.astronaut()) >>> img = color.rgb2gray(img) >>> rng = np.random.default_rng() >>> img += 0.1 * rng.standard_normal(img.shape) >>> img = np.clip(img, 0, 1) >>> denoised_img = denoise_wavelet(img, sigma=0.1, rescale_sigma=True)
- skimage.restoration.ellipsoid_kernel(shape, intensity)[source]#
为 restoration.rolling_ball 创建椭球形核。
- 参数:
- shape类数组
椭圆体主轴的长度(不包括强度轴)。内核需要与将要应用它的图像具有相同的维度。
- intensity整数
椭圆体的强度轴的长度。
- 返回:
- kernelndarray
包含椭球上半部分的表面强度的内核。
另请参阅
- skimage.restoration.estimate_sigma(image, average_sigmas=False, *, channel_axis=None)[source]#
(高斯)噪声标准偏差的稳健的基于小波的估计器。
- 参数:
- imagendarray
要估计噪声标准差的图像。
- average_sigmas布尔值,可选
如果为 true,则平均
sigma的通道估计值。 否则,返回与每个通道对应的 sigma 列表。- channel_axisint 或 None, optional
如果为
None,则假定图像为灰度(单通道)。否则,此参数指示数组的哪个轴对应于通道。0.19 版本中添加:在 0.19 中添加了
channel_axis。
- 返回:
- sigma浮点数或列表
估计的噪声标准差。 如果
multichannel为 True 并且average_sigmas为 False,则返回每个通道的单独噪声估计值。 否则,返回各个通道估计值的平均值。
备注
此函数假定噪声服从高斯分布。 估计算法基于小波细节系数的中值绝对偏差,如 [1] 的 4.2 节中所述。
参考文献
[1]D. L. Donoho 和 I. M. Johnstone。“小波收缩的理想空间自适应。” Biometrika 81.3 (1994): 425-455. DOI:10.1093/biomet/81.3.425
示例
>>> import skimage.data >>> from skimage import img_as_float >>> img = img_as_float(skimage.data.camera()) >>> sigma = 0.1 >>> rng = np.random.default_rng() >>> img = img + sigma * rng.standard_normal(img.shape) >>> sigma_hat = estimate_sigma(img, channel_axis=None)
- skimage.restoration.inpaint_biharmonic(image, mask, *, split_into_regions=False, channel_axis=None)[source]#
使用双调和方程修补图像中被遮盖的点。
- 参数:
- image(M[, N[, …, P]][, C]) ndarray
输入图像。
- mask(M[, N[, …, P]]) ndarray
要进行修复的像素数组。必须与“image”通道之一具有相同的形状。未知像素必须用 1 表示,已知像素用 0 表示。
- split_into_regionsboolean, optional
如果为 True,则按区域进行修复。这可能会较慢,但会减少内存需求。
- channel_axisint 或 None, optional
如果为 None,则假定图像为灰度(单通道)图像。否则,此参数指示数组的哪个轴对应于通道。
0.19 版本中添加:在 0.19 中添加了
channel_axis。
- 返回:
- out(M[, N[, …, P]][, C]) ndarray
带有已修复的遮罩像素的输入图像。
参考文献
[1]S.B.Damelin 和 N.S.Hoang。“On Surface Completion and Image Inpainting by Biharmonic Functions: Numerical Aspects”, International Journal of Mathematics and Mathematical Sciences, Vol. 2018, Article ID 3950312 DOI:10.1155/2018/3950312
[2]C. K. Chui 和 H. N. Mhaskar, MRA Contextual-Recovery Extension of Smooth Functions on Manifolds, Appl. and Comp. Harmonic Anal., 28 (2010), 104-113, DOI:10.1016/j.acha.2009.04.004
示例
>>> img = np.tile(np.square(np.linspace(0, 1, 5)), (5, 1)) >>> mask = np.zeros_like(img) >>> mask[2, 2:] = 1 >>> mask[1, 3:] = 1 >>> mask[0, 4:] = 1 >>> out = inpaint_biharmonic(img, mask)
- skimage.restoration.richardson_lucy(image, psf, num_iter=50, clip=True, filter_epsilon=None)[source]#
理查森-露西反卷积。
- 参数:
- image([P, ]M, N) ndarray
输入退化图像(可以是 n 维)。如果您保留默认的
clip=True参数,您可能需要对图像进行归一化,使其值落在 [-1, 1] 区间内,以避免信息丢失。- psfndarray
点扩散函数。
- num_iterint, optional
迭代次数。此参数起到正则化的作用。
- clipboolean, optional
默认为 True。如果为 true,则为了与 skimage 管道兼容,结果中高于 1 或低于 -1 的像素值会被阈值化。
- filter_epsilon: float, optional
中间结果低于此值将变为 0,以避免除以小数字。
- 返回:
- im_deconvndarray
反卷积图像。
参考文献
示例
>>> from skimage import img_as_float, data, restoration >>> camera = img_as_float(data.camera()) >>> from scipy.signal import convolve2d >>> psf = np.ones((5, 5)) / 25 >>> camera = convolve2d(camera, psf, 'same') >>> rng = np.random.default_rng() >>> camera += 0.1 * camera.std() * rng.standard_normal(camera.shape) >>> deconvolved = restoration.richardson_lucy(camera, psf, 5)
- skimage.restoration.rolling_ball(image, *, radius=100, kernel=None, nansafe=False, num_threads=None)[source]#
通过滚动/平移内核来估计背景强度。
此滚动球算法估计不均匀曝光情况下 ndimage 的背景强度。它是常用的滚动球算法的推广 [1]。
- 参数:
- imagendarray
要过滤的图像。
- radiusint, optional
在图像中滚动/平移的球形内核的半径。如果
kernel = None,则使用此值。- kernelndarray, optional
在图像中滚动/平移的内核。它必须具有与
image相同的维度数。内核填充有该位置的内核强度。- nansafe: bool, optional
如果
False(默认),则假设image中的值都不是np.nan,并使用更快的实现。- num_threads: int, optional
要使用的最大线程数。如果
None,则使用 OpenMP 默认值;通常等于最大虚拟核心数。注意:这是线程数的上限。确切的数字由系统的 OpenMP 库确定。
- 返回:
- backgroundndarray
图像的估计背景。
备注
对于估计了背景强度的像素(不妨在
center处),滚动球方法将kernel放置在其下方,并升高内核,直到表面在某个pos=(y,x)处接触图像伞形部分。然后使用该位置的图像强度 (image[pos]) 加上kernel[center] - kernel[pos]的差来估计背景强度。此算法假定暗像素对应于背景。如果您有明亮的背景,请在将图像传递给该函数之前将其反转,例如,使用
utils.invert。有关详细信息,请参见图库示例。此算法对噪声敏感(特别是椒盐噪声)。如果这在您的图像中是一个问题,您可以在将图像传递给此函数之前应用轻微的高斯平滑。
此算法的复杂度是半径的多项式,次数等于图像维度(2D 图像为 N^2,3D 图像为 N^3 等),因此当半径超过 30 左右时,可能需要很长时间 ([2], [3])。这是一个精确的 N 维计算;如果您只需要近似值,则要考虑的更快选项是顶帽滤波 [4] 或降采样然后升采样以减小处理的输入大小。
参考文献
[1]Sternberg, Stanley R. “Biomedical image processing.” Computer 1 (1983): 22-34. DOI:10.1109/MC.1983.1654163
示例
>>> import numpy as np >>> from skimage import data >>> from skimage.restoration import rolling_ball >>> image = data.coins() >>> background = rolling_ball(data.coins()) >>> filtered_image = image - background
>>> import numpy as np >>> from skimage import data >>> from skimage.restoration import rolling_ball, ellipsoid_kernel >>> image = data.coins() >>> kernel = ellipsoid_kernel((101, 101), 75) >>> background = rolling_ball(data.coins(), kernel=kernel) >>> filtered_image = image - background
- skimage.restoration.unsupervised_wiener(image, psf, reg=None, user_params=None, is_real=True, clip=True, *, rng=None)[source]#
无监督维纳-亨特反卷积。
使用 Wiener-Hunt 方法返回反卷积,其中超参数会自动估计。该算法是下文参考中描述的随机迭代过程(吉布斯采样器)。另请参见
wiener函数。- 参数:
- image(M, N) ndarray
输入退化图像。
- psfndarray
脉冲响应(输入图像空间)或传递函数(傅里叶空间)。两者都被接受。传递函数会自动识别为复数 (
np.iscomplexobj(psf))。- regndarray, optional
正则化算子。默认情况下为拉普拉斯算子。它可以是脉冲响应或传递函数,与 psf 相同。
- user_paramsdict, optional
吉布斯采样器的参数字典。请参见下文。
- clipboolean, optional
默认为 True。如果为 true,则为了与 skimage 管道兼容,结果中高于 1 或低于 -1 的像素值会被阈值化。
- rng{
numpy.random.Generator, int}, optional 伪随机数生成器。默认情况下,使用 PCG64 生成器(请参见
numpy.random.default_rng())。如果rng是一个 int,则将其用于播种生成器。在版本 0.19 中添加。
- 返回:
- x_postmean(M, N) ndarray
反卷积图像(后验平均值)。
- chainsdict
键
noise和prior分别包含噪声和先验精度的链列表。
- 其他参数:
- ``user_params`` 的键是
- thresholdfloat
停止条件:两个连续近似解之间的差的范数(对象样本的经验平均值,请参见“注释”部分)。默认为 1e-4。
- burninint
要忽略以开始计算平均值的样本数。默认为 15。
- min_num_iterint
最小迭代次数。默认为 30。
- max_num_iterint
如果未满足
threshold,则最大迭代次数。默认为 200。- callback可调用 (默认为 None)
用户提供的可调用对象,如果函数存在,则将当前图像样本传递给它以用于任何目的。用户可以存储样本,或计算平均值以外的其他矩。它对算法执行没有影响,仅用于检查。
备注
估计图像被设计为概率定律(来自贝叶斯分析)的后验均值。该均值定义为所有可能图像的总和,并根据其各自的概率加权。考虑到问题的大小,精确求和是难以处理的。此算法使用 MCMC 在后验定律下绘制图像。实际的想法是仅绘制高概率的图像,因为它们对均值的贡献最大。相反,不太可能的图像被绘制的次数较少,因为它们的贡献较低。最后,这些样本的经验均值给出了均值的估计,并且是无限样本集的精确计算。
参考文献
[1]François Orieux, Jean-François Giovannelli, and Thomas Rodet, “贝叶斯估计维纳-亨特反卷积的正则化和点扩散函数参数”, J. Opt. Soc. Am. A 27, 1593-1607 (2010)
https://www.osapublishing.org/josaa/abstract.cfm?URI=josaa-27-7-1593
示例
>>> from skimage import color, data, restoration >>> img = color.rgb2gray(data.astronaut()) >>> from scipy.signal import convolve2d >>> psf = np.ones((5, 5)) / 25 >>> img = convolve2d(img, psf, 'same') >>> rng = np.random.default_rng() >>> img += 0.1 * img.std() * rng.standard_normal(img.shape) >>> deconvolved_img = restoration.unsupervised_wiener(img, psf)
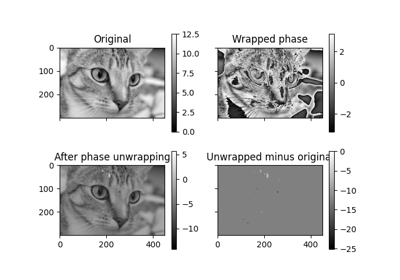
- skimage.restoration.unwrap_phase(image, wrap_around=False, rng=None)[源代码]#
从包裹的相位图像中恢复原始图像。
从一个包裹在区间 [-pi, pi) 中的图像中,恢复原始的、展开的图像。
- 参数:
- image(M[, N[, P]]) ndarray 或浮点数类型的掩码数组
这些值应在 [-pi, pi) 范围内。 如果提供掩码数组,则不会更改掩码条目,并且它们的值将不会用于引导相邻的、未掩码的值的展开。 不允许使用掩码的 1D 数组,并且会引发
ValueError。- wrap_around布尔值或布尔值序列,可选
当序列的元素为
True时,展开过程会将图像的相应轴的边缘视为连接的,并使用此连接来引导相位展开过程。如果仅给出单个布尔值,它将应用于所有轴。1D 数组不支持环绕。- rng{
numpy.random.Generator, int}, optional 伪随机数生成器。默认情况下,使用 PCG64 生成器(请参见
numpy.random.default_rng())。如果rng是一个 int,则将其用于播种生成器。展开依赖于随机初始化。 这将设置用于实现确定性行为的 PRNG。
- 返回:
- image_unwrappedarray_like,双精度
与输入形状相同的展开图像。如果输入
image是一个掩码数组,则将保留掩码。
- 引发:
- ValueError
如果使用掩码的 1D 数组调用,或者使用 1D 数组和
wrap_around=True调用。
参考文献
[1]Miguel Arevallilo Herraez, David R. Burton, Michael J. Lalor, 和 Munther A. Gdeisat, “基于可靠性排序的快速二维相位展开算法,遵循非连续路径”, Journal Applied Optics, Vol. 41, No. 35 (2002) 7437,
[2]Abdul-Rahman, H., Gdeisat, M., Burton, D., & Lalor, M., “基于可靠性排序的快速三维相位展开算法,遵循非连续路径。在 W. Osten, C. Gorecki, & E. L. Novak (Eds.), Optical Metrology (2005) 32–40, International Society for Optics and Photonics.中。
示例
>>> c0, c1 = np.ogrid[-1:1:128j, -1:1:128j] >>> image = 12 * np.pi * np.exp(-(c0**2 + c1**2)) >>> image_wrapped = np.angle(np.exp(1j * image)) >>> image_unwrapped = unwrap_phase(image_wrapped) >>> np.std(image_unwrapped - image) < 1e-6 # A constant offset is normal True
- skimage.restoration.wiener(image, psf, balance, reg=None, is_real=True, clip=True)[源代码]#
维纳-亨特反卷积
返回使用维纳-亨特方法(即使用傅立叶对角化)的反卷积。
- 参数:
- imagendarray
输入降级的图像(可以是 n 维的)。
- psfndarray
点扩散函数。 如果数据类型是实数,则假设这是脉冲响应(输入图像空间);如果数据类型是复数,则假设这是传递函数(傅立叶空间)。 脉冲响应的形状没有约束。 如果
is_real 为 True,则传递函数的形状必须为(N1, N2, ..., ND);否则为(N1, N2, ..., ND // 2 + 1)(请参阅np.fft.rfftn)。- balance浮点数
正则化参数值,用于调整数据充分性(提高频率恢复)和先验充分性(减少频率恢复以避免噪声伪影)之间的平衡。
- regndarray, optional
正则化算子。 默认情况下为拉普拉斯算子。 它可以是脉冲响应或传递函数,与 psf 相同。 形状约束与
psf参数相同。- is_real布尔值,可选
默认情况下为 True。指定是否使用埃尔米特假设提供
psf和reg,即仅提供一半的频率平面(由于实信号的傅立叶变换的冗余)。 仅当psf和/或reg作为传递函数提供时才适用。 有关埃尔米特属性,请参阅uft模块或np.fft.rfftn。- clipboolean, optional
默认情况下为 True。 如果为 True,则为了实现 skimage 管道兼容性,将对结果中高于 1 或低于 -1 的像素值进行阈值处理。
- 返回:
- im_deconv(M, N) ndarray
反卷积图像。
备注
此函数将维纳滤波器应用于被脉冲响应(或 PSF)噪声和降级的图像。 如果数据模型是
\[y = Hx + n\]其中 \(n\) 是噪声,\(H\) 是 PSF,\(x\) 是未知的原始图像,则维纳滤波器是
\[\hat x = F^\dagger \left( |\Lambda_H|^2 + \lambda |\Lambda_D|^2 \right)^{-1} \Lambda_H^\dagger F y\]其中 \(F\) 和 \(F^\dagger\) 分别是傅立叶变换和傅立叶逆变换,\(\Lambda_H\) 是传递函数(或 PSF 的傅立叶变换,请参阅下面的 [Hunt]),\(\Lambda_D\) 是惩罚恢复的图像频率的滤波器(默认情况下为拉普拉斯算子,即惩罚高频)。 参数 \(\lambda\) 调整数据(趋于增加高频,即使是来自噪声的高频)和正则化之间的平衡。
然后,这些方法特定于先验模型。 因此,应用程序或真实图像的性质必须与先验模型相对应。 默认情况下,先验模型(拉普拉斯算子)引入图像平滑性或像素相关性。 它也可以解释为高频惩罚,以补偿解相对于数据的不稳定性(有时称为噪声放大或“爆炸式”解)。
最后,傅立叶空间的使用意味着 \(H\) 的循环属性,请参阅 [2]。
参考文献
[1]François Orieux, Jean-François Giovannelli, and Thomas Rodet, “贝叶斯估计维纳-亨特反卷积的正则化和点扩散函数参数”, J. Opt. Soc. Am. A 27, 1593-1607 (2010)
https://www.osapublishing.org/josaa/abstract.cfm?URI=josaa-27-7-1593
[2]B. R. Hunt “离散卷积定理的矩阵理论证明”,IEEE Trans. on Audio and Electroacoustics, vol. au-19, no. 4, pp. 285-288, dec. 1971
示例
>>> from skimage import color, data, restoration >>> img = color.rgb2gray(data.astronaut()) >>> from scipy.signal import convolve2d >>> psf = np.ones((5, 5)) / 25 >>> img = convolve2d(img, psf, 'same') >>> rng = np.random.default_rng() >>> img += 0.1 * img.std() * rng.standard_normal(img.shape) >>> deconvolved_img = restoration.wiener(img, psf, 0.1)